新疆H1N1甲型流感疫情预测模型的比较研究

新疆大学数学与系统科学学院(830046) 胡 兴 胡锡健

新疆H1N1甲型流感疫情预测模型的比较研究

新疆大学数学与系统科学学院(830046) 胡 兴 胡锡健

本文针对2009年9月6日至11月17日新疆的甲流病例数据，用多种统计方法建立了数学模型，通过对几种方法的比较以期得到理想的预测模型，数据来源于政府官方网站。

1.甲流病例数据的定性分析

反映甲流疫情的指标有每日新增病例数、累积病例数、病死率、累积疑似病例数等。

新疆2009年9月6日至11月17日甲流累积病例数与每日新增病例数的图像，如图1，2所示。

图1 新疆HIV1甲型流感累计病例数

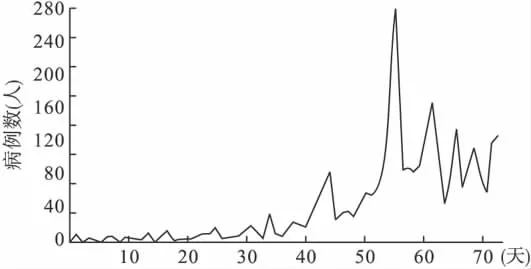
图2 新疆HIV1甲型流感每日新增病例数

甲流一般为三个阶段：发展期，抑制期和衰退期。在发展期时，由于疾病产生初期医疗手段还不能有效的控制疫情，所以累积患病人数会持续走高且每日新增发病人数也逐天上升;在抑制期，由于医疗手段已相对成熟，虽然累积人数还在上升，但是每日新增患病人数已经开始逐渐下降，疫情已经得到控制;在衰退期时，每日新增患病人数基本为零，这时累积患病人数也开始逐渐下降直至降为零。从图1，2可以看出，新疆累积患病人数还在持续走高，而每日新增患病人数已经开始明显下降，故可以认为新疆的疫情已经基本处在抑制期。

2.甲流累积病例数据的定量分析

从累积病例数据的时序图上可以看出，累积病例数据可能服从指数曲线模型或S曲线模型。下面我们用指数曲线模型，S曲线模型及时间序列中的ARMA(p，q)模型来分别建立预测模型，对这几种方法进行比较后得出最佳的预测方法。

(1)指数曲线模型

指数曲线预测模型如下：

其中，a，b为待定参数。计算得 yt=28.07e0.065t，拟合度为0.985。拟合曲线见图3。

模型的拟合优度，模型的拟合图都很好，所以用指数模型来预测现阶段的疫情发展其结果比较好。

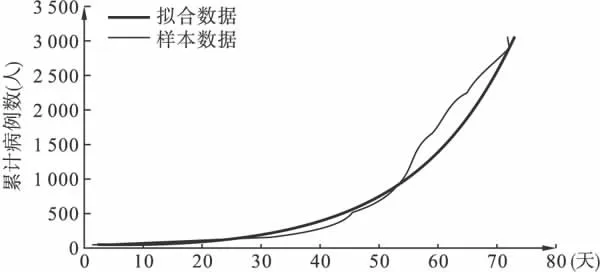
图3 甲流积累病例数据曲线拟合图

(2)S曲线模型

S曲线预测模型如下：

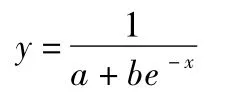
其中，a，b为待定参数。计算得

回归模型的系数为a=0.006，b=0.068，但是拟合优度仅为0.201，用S曲线来预测疫情的发展其结果并不理想。

(3)ARMA(p，q)模型

由自回归和移动平均两部分共同构成的随机过程称为自回归移动平均过程，即为ARMA(p，q)。其中p，q分别表示自回归和移动平均部分的最大阶数。

利用Box-Jenkins建模思想来对数据进行建模，可分为四个步骤：

①平稳性检验

使用EViews软件对原数据进行ADF检验，检验结果显示，原序列以较大的概率(P=0.9994)接受原假设，即存在单位根的结论。将原序列做1阶差分，然后对差分后的序列进行ADF检验，检验结果显示，差分后的序列在0.01的检验水平下拒绝原假设，接受不存在单位根的结论，因此可以确定原序列是经1阶差分后的序列是一个平稳序列。

②确定ARMA模型的阶数p和q

我们对一阶差分后的序列采用AIC准则来确定模型的阶。取T/10，ln(T)分别作为p，q的滞后上限，其中T为样本容量。由于原序列的样本量为73，故差分后的样本容量T=72。p=1，2，3，4，5，6，7;q=1，2，3，4。使用 EViews 软件计算得到当p=7，q=2时模型的AIC值最小，为9.24。对差分后的序列进行ARMA(7，2)的模型参数估计，并检验参数的统计学意义。

③估计检验模型位置参数

经EViews软件计算得到回归系数和各t-统计量，经检验均有统计学意义，拟合度达到了0.83。

④进行诊断分析

回归方程如下：

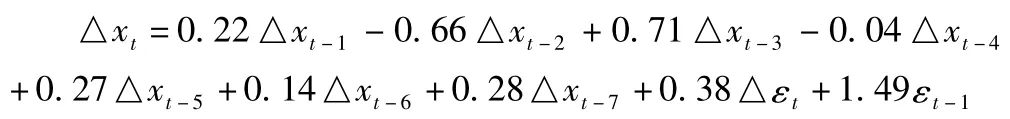
把上面得到的回归方程转换成原序列的形式：

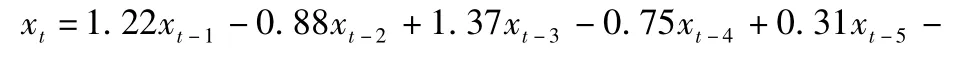
对残差序列进行序列相关性检验考察模型本身的合理性，结果显示残差不存在序列相关。预测结果与原序列的比较结果如图4。

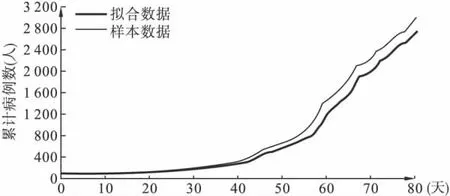
图4 甲流累积病例预测结果与原序列的比较

通过对以上三个模型的建立，可以看出在现阶段使用指数模型和ARMA(p，q)模型均能取得不错的预测效果，可以对现阶段的疫情发展做出较为准确的预测。

1.张剑湖，叶锋.SARS的传播预测模型研究，中国系统工程学会全面建设小康社会和系统过程会议论文集(母体文献)，2004：715-720.

2.王建锋.SARS流行预测分析，中国工程科学，2003，5(8)：23-28.

3.Development of mathematical models(Logistic，Gompertz and Richards models)describing the grow th pattern of Pseudomonas putida(NICM 2174)，Bioprocess Engineering，2000(23)：607-612.