可拓聚类方法在医院年收治病人数预测中的应用*

潍坊医学院公共卫生学院(261053) 黎景雪 潘庆忠 房 刚 王培承

可拓聚类方法在医院年收治病人数预测中的应用*

潍坊医学院公共卫生学院(261053) 黎景雪 潘庆忠 房 刚 王培承△

目的将可拓聚类方法用于对医院年收治病人数的预测。方法 构造可拓聚类预测模型，判断待聚类样本所属类别，对其进行预测。结果 利用1981～1989年的相关因素数据资料构造可拓聚类预测模型，对1990年的收治病人数进行预测，结果与实际相符。结论 可拓聚类方法用于对医院年收治病人数的预测是有效可行的，可以为医院管理与统计提供一种新的方法。

可拓聚类方法 医院年收治病人数 关联函数

*：2009年潍坊医学院研究生创新基金项目

△通讯作者

可拓学是由我国学者蔡文于1983年创立的一门新学科，它从定性和定量两个角度去研究解决矛盾问题的规律和方法，为广大实际工作者，尤其是管理、决策和设计人员提供一种启发性的思想与分析方法。可拓聚类预测就是根据事物关于特征的量值来判断其属于某一类的程度，通过计算关联函数使聚类定量化。近年来，可拓聚类预测方法已经在工程类学科中广泛应用，但在医学领域的应用尚不多见，本文在这方面进行尝试，为医学领域提供一种新的预测方法。

医院年收治病人数是反映医院工作量的一个重要指标，其大小直接影响医院的社会效益和经济效益，它和多种因素有关。本文利用可拓聚类预测方法对医院年收治病人数做出科学合理的预测，为医院决策管理提供依据。

原理与方法〔1-4〕

1.原理

可拓学中物元的概念为解决聚类分析问题提供了新的思路，其根据事物关于特征的量值来判断此事物属于某一集合的程度。可拓聚类预测方法首先通过聚类分析划分集合P的若干子集，然后构造经典域物元和节域物元，对于待测物元，通过计算关联函数值确定其属于哪个子集，从而得到可拓聚类预测的结果。

2.方法

设Ii(i=1，2，…，m)是P的m个子集，Ii⊂P(i=1，2，…，m)，对任何待测对象p⊂P，用以下步骤判断p属于哪个子集Ii，并计算p隶属于任一子集Ii的程度。

(1)确定经典域物元和节域物元

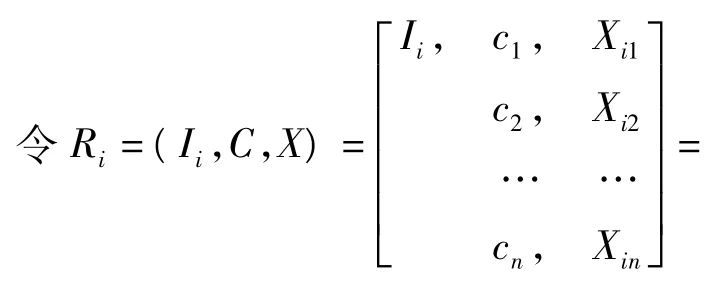
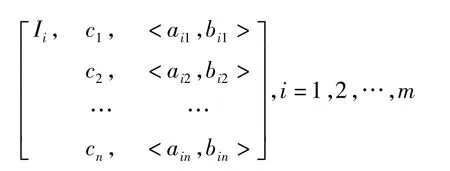
其中，c1，c2，…，cn是Ii的n个不同特征，Xi1，Xi2，…，Xin分别为Ii关于特征c1，c2，…，cn的取值范围，即经典域。并且有Xij= ＜aij，bij＞(j=1，2，…，n)。

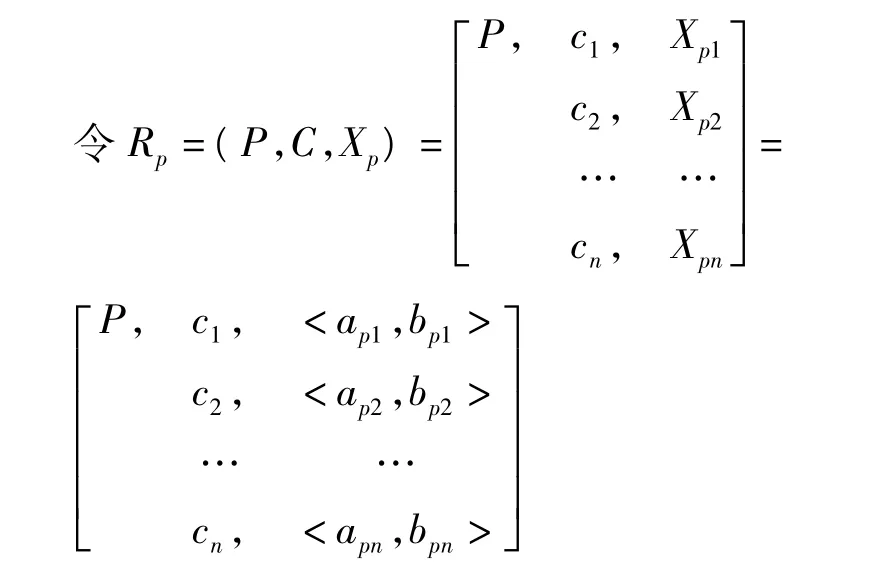
其中，Xp1，Xp2，…，Xpn分别是P关于特征c1，c2，…，cn的取值范围，即P的节域。并且有Xpj=＜apj，bpj＞(j=1，2，…，n)。

待测样本形成的物元为

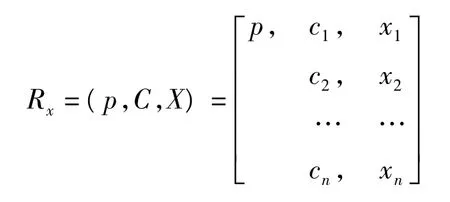
其中，x1，x2，…，xn分别为待测样本的n个因子的观测值。

(2)确定关联函数并计算关联函数值

待测样本与各类的关联度按下列公式计算：

其中x0为K(x)取最大值的点，ρ(xj，Xij)和 ρ(xj，Xpj)称为点与区间的距，其计算公式为：

(3)确定权系数并计算隶属程度

权系数的大小对于综合关联度的高低具有举足轻重的作用，为了尽量合理地确定权系数，可以使用层次分析法〔5，6〕来确定各个因子之间的相对重要性次序，从而计算出综合关联度。

则待测样本p对i类的综合关联度为：

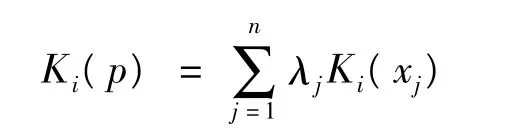
(4)判定待测样本p所属类别

若Ki=maxKi(p)，i=1，2，…，m，则判定样本p属于i类;若对一切i，Ki(p)≤0，则表示样本p已不在所划分的类别之内。

实例分析

医院年收治病人数和多种因素有关，在此选取5个因素进行分析，资料见表1〔7〕。利用1981～1989年的数据建立可拓聚类预测模型的经典域物元和节域物元，将1990年的数据作为待测物元，对1990年的医院年收治病人数进行区间预测。具体过程如下：

1.资料处理

某医院1981～1990年收治病人数和可能影响因素的原始资料如表1所示，在此先计算出年收治病人数和各个影响因素的年增长率数据，这里的年增长率定义为该年的值与上一年的值之比〔3〕。

表1 某院1981～1990年收治病人数和可能影响因素的原始数据及年增长率

将1982～1989年的数据作为聚类样本，1990年作为待测年。由表1数据可以看出，收治病人数的年增长率在0.90～1.16之间，将样本数据按照收治病人数的年增长率 R 分为3类：I1：0.90＜R≤0.99，I2：0.99＜R≤1.08，I3：1.08＜R≤1.17。统计各类的样本数并计算其因子(影响因素)均值，如表2所示。

2．确定经典域物元和节域物元及待测样本物元

结合表1的年增长率数据和表2的因子均值数据构造各类的经典域物元以及节域物元，并确定待测样本物元。通过观察发现，各个因子的最大值均小于1.20，所以我们将节域的最大值确定为1.20，节域的最小值确定为各个因子的最小值，并且同一因子的各个经典域的区间并集为节域。

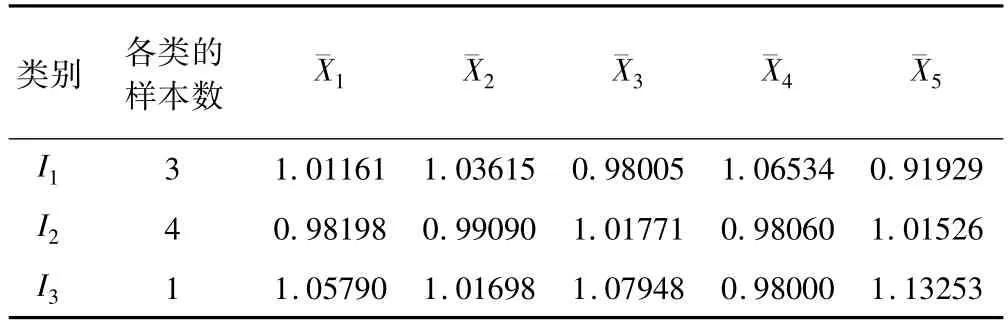
表2 医院收治病人数年增长率的各类样本数及因子均值

经典域物元为：

3.计算待测样本对各类的关联度

根据上述方法中的相关公式进行计算，最后结果如表3所示。因为X1，X2，X3和X5四个因子与年收治病人数成正向相关，即在一个区间内取值越大越好，所以我们选择右侧距最大值在端点b的公式进行计算，反之，因子X4选择左侧距最大值在端点a的公式进行计算。各个因子的权重用层次分析法来确定。

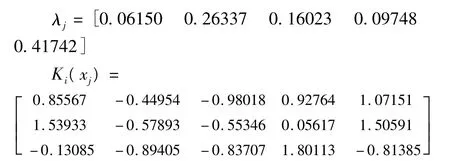
表3 待测样本与各类的综合关联度及聚类预测结果

讨 论

从关联度和聚类预测结果可以看出，1990年的医院收治病人数年增长率属于第二类，即在0.99～1.08之间，而1990年的收治病人数实际年增长率为1.05971，恰好在第二类的范围之内，所以用可拓聚类方法预测医院年收治病人数是有效的。

用可拓学的理论和方法对医院收治病人数进行预测是一种尝试。它可以把多个影响因素综合起来作为一个物元进行分析，其计算较为简单，具有较强的实用性。而且该方法对样本含量没有严格的限制，预测精度不会受到样本含量的影响。需要注意的是，该方法中关联函数的选择至关重要，不适合的关联函数会导致错误的结论，另外，权系数的确定也是一个关键问题，所得到的权系数必须客观、真实地反应实际情况。

1.蔡文.物元模型及其应用.北京：科学技术文献出版社，1994.

2.周法莲，郭秀花.可拓综合评判在流脑发病率预测中的应用.数理医药学杂志，1998，11(1)：84-85.

3.高洁.可拓聚类预测方法及其在邮电业务总量预测中的应用.系统工程，2000，18(3)：73-77.

4.王超.可拓聚类模型在集装箱生成量预测中的应用.物流科技，2008，10：34-36.

5.孙振球.医学综合评价方法及其应用.北京：化学工业出版社，2006：49-52.

6.吕荣爱，张凤桃.综合评价医疗效果与效率.中国卫生统计，2007，24(1)：90-91.

7.尹慧颖，刘勖.关联度分析在医院年收治病人数影响因素研究中的应用.中国医院统计，1994，1(3)：137-140.