列联表资料的关联强度*

薛允莲 姜世强 刘贵浩 张晋昕

列联表资料的关联强度*

薛允莲1姜世强2刘贵浩3张晋昕4△

目的探究行列数为2-4的各列联表Pearson列联系数的分布及其与相关系数的关系。方法 采用SAS 9.1.3软件模拟行列数分别为2-4，且行合计固定的各种列联表，计算相关系数和列联系数，绘制两者的散点图，描述其取值变化关系。结果 2×2列联表的相关系数和列联系数成曲线相关，但是其他情况下相关系数和列联系数的关系并非一一对应，此时通过相关系数划分列联系数的关联强度是不合适的。结论 对于2×2列联表，可以通过相关系数的强度范围近似定义列联系数的强度范围。当行列数多于2时，不能根据相关系数的强度范围定义列联系数的强度范围。

列联表 列联系数 相关系数 关联强度

*：中山大学教学改革研究课题(编号：中大教务〔2009〕108号-26)

1.中山大学孙逸仙纪念医院(510120)

2.深圳市南山区疾病预防控制中心(518054)

3.广东省健康教育研究所(510120)

4.中山大学公共卫生学院医学统计与流行病学系(510080)

△通讯作者：张晋昕，E-mail：zhjinx@mail.sysu.edu.cn

医学研究中常采用列联系数计算列联表资料的关联强度，这在一定程度上克服因样本量过多或过少导致χ2值被过低或过高估计的缺陷〔1-3〕。常用的列联系数有Phi(φ)，ContingencyCoefficientr和Cramer’sV。

(1)Phi通常用于二分法形成的四格表资料相关性的测量。对于多维频数表，Phi的最大值依赖于频数表的维数，并且绝对值会超过1，这使得Phi不是测量相关性完全合适的方法。(2)Pearson列联系数(ContingencyCoefficientr)是对Phi的校正，目的是使相关性测量可以应用于多维列联表资料。r值虽然控制了样本含量的影响，但其大小受到列联表维数的影响，对于低维列联表r的最大值小于1。(3)列联系数r更适合于行列数相同时的列联表资料，当行列数不同时可以参考Cramer提出的列联系数的修正方法(Cramer’sV)进行修正。V取值在［0～1］之间，对于相同维数的列联表资料，V值较Phi和Pearson系数小。V值受到列联表边缘合计的影响，边缘合计的数值越大，V值越偏离1，仅当两变量的边缘合计相等时，V值可达到1。所以V值也不是测量相关程度的可靠方法。

李克均等〔4〕认为一个满意的相关度量应至少具备下列两个特点：(1)当两变量显示出完全不相关时，系数应该等于0;(2)当两变量显示出完全正相关时，系数应该等于1。Pearson列联系数r具有第一个特点但没有第二个特点，使其在测量关联强度时受到一定限制。但是，综合以上三种列联系数的特点可知，Pearson列联系数r消除了样本含量的影响，且绝对值不会超过1，是判断行列数相等的列联表资料关联强度较为合适的方法。实际应用中也较多采用Pearson列联系数计算列联表资料的关联强度。

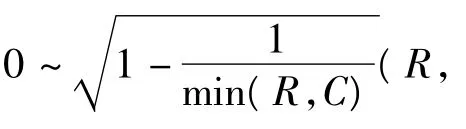
资料与方法

采用SAS9.1.3〔9〕软件分别模拟行列数为2-4的列联表，使每个列联表的行百分比出现从0-1的各种情况组合的数据。本文一共模拟并计算了8种情况下列联表资料相关系数和列联系数的散点图。

虽然列联表资料的相关性不适合采用相关系数进行描述，但是本文为了说明列联系数的关联强度，以绝对值［0，1］的相关系数为参照，计算同一列联表的列联系数和相关系数的关系。相关系数的计算是采用对频数列加权的方式进行。

模拟R×C列联表资料和计算相关系数、列联系数的SAS程序见附录。

结 果

图1～图8列出了行列数为2-4时R×C列联表的相关系数和列联系数的散点图，横轴为列联系数，纵轴为相关系数。

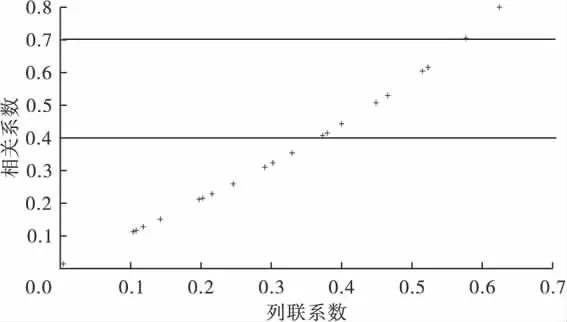
图1 2×2列联表的相关系数和列联系数的散点图

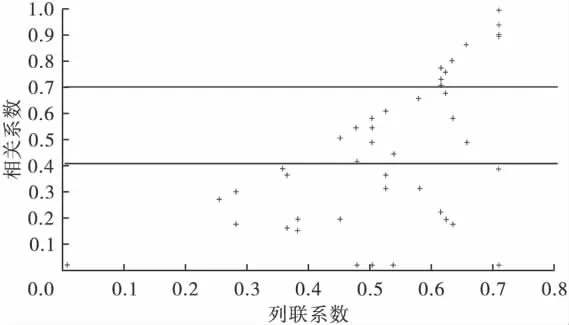
图2 2×3列联表的相关系数和列联系数的散点图

图3 2×4列联表的相关系数和列联系数的散点图

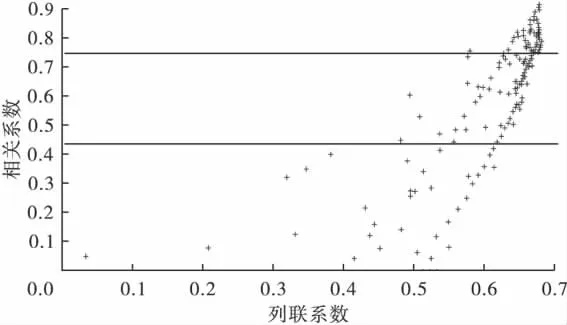
图4 3×2列联表的相关系数和列联系数的散点图

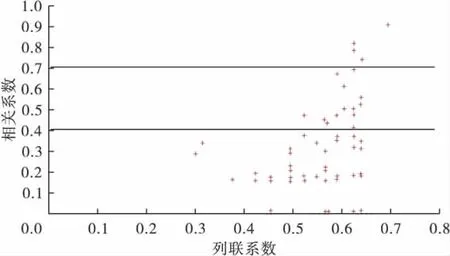
图5 3×3列联表的相关系数和列联系数的散点图

图6 3×4列联表的相关系数和列联系数的散点图

图7 4×3列联表的相关系数和列联系数的散点图

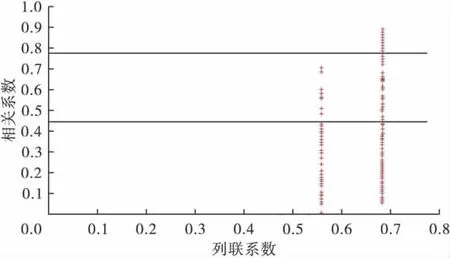
图8 4×4列联表的相关系数和列联系数的散点图

可见，对于2×2列联表资料，相关系数和列联系数是曲线形式的一一对应关系。通过图形1可以大致确定2×2列联表资料列联系数的最大取值为0.707，可以通过相关系数密切程度的范围〔4〕——［0，0.4)为低度相关、［0.4，0.7)为中度相关、［0.7，1］为高度相关，近似确定列联系数的密切程度范围——［0，0.36)为低度相关、［0.36，0.56)为中度相关、［0.56，0.71］为高度相关。

当行数或列数多于2时，相关系数和列联系数并非一一对应，而是呈现扩散或收敛状的对应关系。模拟序列情况可知，多数散点集中在列联系数较大的位置。所以，对于行数或列数超过2的列联表资料，不能基于列联系数判定关联密切程度。

讨 论

在进行列联表资料关联性的度量时，医学工作者需要正确使用列联系数，不能简单地以［0，1］作为所有维数列联表资料关联性的取值范围，更不能以相关系数关联强度的划分范围来定义列联系数的关联强度。

对于四格表资料，因为列联系数和相关系数呈一一对应的曲线关系，可以参考本文通过SAS程序绘制的散点图计算得到列联系数关联强度的区间。但是对于列数或行数多于2的列联表资料，因为相关系数和列联系数并非呈现一一对应的关系，所以不能简单地像通过相关系数反映关联强度的做法那样，试图基于列联系数反映其关联强度。

1.Roscino A，Pollice A.A Generalization of the Polychoric Correlation Coefficient.Dipartimento di Scienze Statistiche，2005：135-142.

2.Non-parametric Measures of Bivariate Relationships.http：//www.unesco.org/webworld/idams/advguide/Chapt4_2.htm.

3.Nominal Association：Phi，Contingency Coefficient，Tschuprow's T，Cramer's V，Lambda，Uncertainty Coefficient.http：//www2.chass.ncsu.edu/garson/pa765/assocnominal.htm.

4.李克均，时松和，胡东生.列联表的行列关联度与对应分析.中国卫生统计，2006，23(3)：261-263.

5.方积乾主编.卫生统计学.第5版.北京：人民卫生出版社，2003：213-214.

6.方积乾主编.医学统计学与电脑实验.上海：上海科学技术出版社，2006：96-98.

7.方积乾主编.生物医学研究的统计方法.北京：高等教育出版社，2007：160-163.

8.武建虎，贺佳，贺宪民，等.关联规则及其在肝癌病人资料分析中的应用.中国卫生统计，2006，23(1)：34-38.

9.SAS9.1.3在线指导手册.http：//support.sas.com/onlinedoc/913/docMainpage.jsp.

附录

1./*固定行合计值的情况下，模拟产生各种数据组合的R×C列联表资料*/

/*给定不同行列数的列联表资料的参数取值，其中nrow为行数，ncol为列数，value为最小值和最大值的合计，low为每个格子的最小可能取值，high为每个格子的最大可能取值*/

2./*分别计算每个R×C表的列联系数和相关系数*/

Association Strength of Contingency Table

XueYunlian，JiangShiqiang，LiuGuihao，etal．SunYat-senmemorialHospitalSun Yat-senuniversity(510120)，Guangzhou

Objective To explore the distribution of Pearson contingency coefficients and their relationship with correlation coefficients.MethodsUsing SAS 9.1.3 software to simulate tables with row or column of 2-4 respectively when fixed row totals.Compute Pearson contingency coefficients and correlation coefficients of each table.Draw scatter plots of Pearson contingency coefficients and correlation coefficients to describe their relationship.ResultsThe scatter plot of correlation coefficients and Pearson contingency coefficients is a curve for 2×2 contingency table.However，for others there are no one-to-one correspondence relationship between correlation coefficients and Pearson contingency coefficients.It is impossible using Pearson contingency coefficients to determine association strength.ConclusionOne can determine intensity of association for Pearson contingency coefficients through correlation coefficients for 2×2 contingency table.But it makes no sense for the other contingency tables.

Contingency table;Pearson contingency coefficient;Correlation coefficient;Association strength

·应用研究·