小脑基因表达数据的模糊多尺度聚类分析*

陈 军 潘 艳 唐世星 张吉强 刘 岭 张彦琦 易 东△

小脑基因表达数据的模糊多尺度聚类分析*

陈 军1潘 艳2唐世星3张吉强4刘 岭1张彦琦1易 东1△

目的为了更好地建立符合生物学意义的基因归类，为一些未知基因的功能提出解释提供参考。方法首先对小脑组织随机抽取100组预处理后的基因表达数据，对每个由7个时间点所成的基因表达信号做多尺度分析，其次在各个尺度下运用改进的FCM算法设计了一个归类阀值，并利用模糊聚类Xie-Beni指数得到了最优聚类数并实现各个尺度下小脑组织基因的聚类，并把每一层对应的聚类结果输出到文本文件，最后找出各层聚类结果完全一致的基因进行归类并进行生物学解释。结果 得到的小脑组织基因最优聚类数为3类，通过分类结果对照发现，各类中的大多数基因生物学意义接近。结论 运用多尺度分析并结合FCM算法应用于基因聚类是有效的，结果具有一定生物学意义，能对生物学基因聚类及基因功能解释具有一定指导作用。

多尺度分析 FCM算法 Xie-Beni指数 聚类 基因

*：国家自然科学基金(No.30872184)

1.第三军医大学卫生统计学教研室(400038)

2.重庆师范大学生命科学学院(401331)

3.承德石油高等专科学校数理系(067000)

4.第三军医大学神经生物学教研室(400038)

△通讯作者：易东，E-mail：yd_house@hotmail.com

聚类分析是大规模基因表达谱目前使用最广泛的统计技术，主要任务是将具有相似表达模式的基因进行归类，从而发现特征相似或生物功能相似的一组基因，使人们更深入地认识诸多生物现象的本质，如基因功能、发育、癌症和药理等。聚类分析也是探索未知基因功能的重要工具，且是后续研究的基础。其中模糊C均值(FCM)聚类算法是目前对基因分类比较好的一种方法〔1，2〕。

目前几乎所有的聚类方法都属于硬聚类，即每个样本最后归类时都属于非此即彼，类与类之间没有交集。但从生物学角度看，对其进行非此即彼的严格划分并不符合生物学自然规律，某些基因可能属于多个类别，参与多个生物过程或生物过程中的调控，因此针对于这个问题我们需找到一些更符合生物学特点的归类方法。本文在此基础上提出了一种新的聚类思路，将FCM聚类算法进行了改进并引入了小波多尺度分析思想，将其应用于胎儿小脑基因表达数据的聚类分析，来实现这一目标。其综合思路是将基因表达信号分解成多个尺度成分(或层)，从宏观到微观进行综合分析，若探讨某两个基因是否可以聚为一类可以从这两个基因的表达信号的各个尺度下的一个变化趋势进行综合考虑，也就是从宏观到微观的变化趋势进行一个综合考虑，如果这两个基因在各个尺度下的变化趋势一致，我们完全有理由认为它们可以聚为一类，这样就更有效地分离出有相近生物学功能或调控的基因;而利用FCM聚类算法确定的最终隶属度矩阵确定一个阀值我们可以实现在每一个尺度成分下基因聚类的软划分，即某个基因可以同时归属于几个类别，这样更加符合生物学特点。

多尺度分析作为数据处理和现象分析的一种重要统计方法，国内外学者对此做了比较系统的理论研究〔3-5〕。由于其数据处理和现象分析全面，其应用前景十分广阔。而各种聚类方法一般需要预先给定聚类数，这对于在大多数情况下聚类数是未知的基因表达数据很不适用，因此本文还对FCM聚类算法使用Xie-Beni指数作为聚类结果的评价指标〔6〕，使用Matlab软件进行了仿真得到最优聚类数，并对结果进行了生物学解释。

多尺度模型及FCM聚类算法

1.多尺度分析

多尺度分析源于傅里叶变换，但其理论研究和实际应用领域已经远远超过傅里叶变换。在理论方面，该方法主要是建立在小波多分辨率分析及Mallat分解及重构算法之上的;在应用方面，多尺度分析必须要选择好小波函数，确定分解及重构层数〔7〕。现在，多尺度分析的应用领域非常广泛，对于具有多层尺度特性的具体问题，都可以尝试建立多尺度分析，此时，是建立了一个小波分析的多尺度模型，即是建立了一个从宏观到微观的空间几何模型。广义上说，多尺度模型包含了空间尺度、时间尺度及语义尺度等〔8〕。

对于一列信号，记为s，对其进行小波多尺度分析，即指对信号进行多个尺度的分解与重构，从不同的尺度分析其信号的方法。下面以对s进行三层多尺度分析来说明其原理。如图1所示，对于信号s，通过小波变换分解为a1和d1，a1称为近似系数，或者从频率上称为低频部分;d1称为细节系数，从频率上称为高频部分。a1中含有原始信号s的有用成分较多，能够起到有效的近似替代原始信号s的作用，而d1则代表了噪声。在第一层上，我们有s=a1+d1。要是需要做更细的划分，我们可以将低频部分d1再次分解为a2和d2，同理可以再将第二层的低频部分a2再次分解为a3和d3。以此类推，如果进行更多尺度的分解，则有ak=ak+1+dk+1。

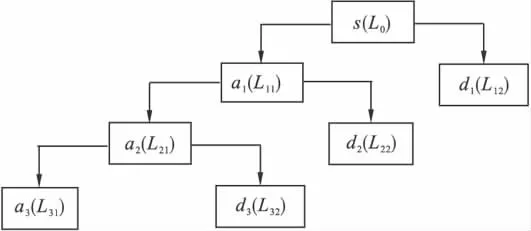
图1 三层多尺度分解示意图

若要将信号完全重构，则有

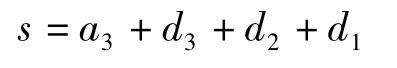
在实际应用中，我们一般根据需要先确定分解和重构的层数。如果去掉某些高频部分，则可达到降噪的目的。当原始信号的噪声不是很强时，我们可以只去掉很少一部分的噪声信息，这样可以保留更多的原始信号。

2.FCM聚类算法

(1)FCM聚类算法的优点

①从生物学角度看，某些基因可能与多个类别高度相关，对其进行非此即彼的严划分不符合自然规律。

②由于生物样本对象和实验因素的影响，在微阵列数据中存在大量噪音数据，而模糊聚类具有很强的噪音鲁棒性，能够在一定程度上减少噪音数据带来的影响。已有文献以FCM法为例详细论证了模糊聚类的噪音鲁棒性。

鉴于以上两个方面的原因，我们认为模糊聚类更适合于对基因表达数据进行分析。

(2)改进的FCM聚类模型

FCM聚类算法，即模糊ISODATA，是用隶属度确定每个数据点属于某个聚类的程度的一种聚类算法。FCM算法是一种柔性的模糊划分，其思想是使得被划分到同一簇的对象之间相似度最大，而不同簇之间的相似度最小。FCM算法的目标函数的一般形式为：

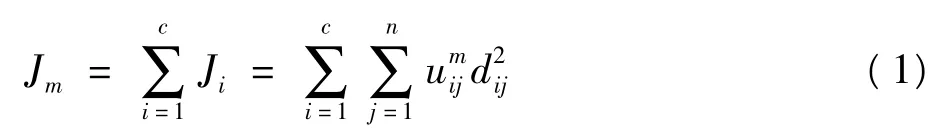
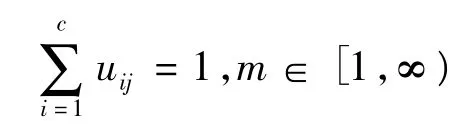
(3)Xie-Beni指数

模糊聚类的最主要不足在于无论所给的聚类数如何，它总能将样本集进行分类，因此大多数聚类算法需要事先确定样本集的分类数。关于样本集的最优分类数问题属于聚类有效性问题，文献〔10〕指出Xie-Beni指数是一种具有较好效果的模糊聚类有效性指标，其计算公式如下：

并且当聚类数c取得对应最优类数c*时，V值最小。文献〔11〕指出加权指数m的取值不仅与给定样本集的结构有关，而且与样本的模糊划分有关，此处我们取加权指数m=2。即Xie-Beni指数公式为：

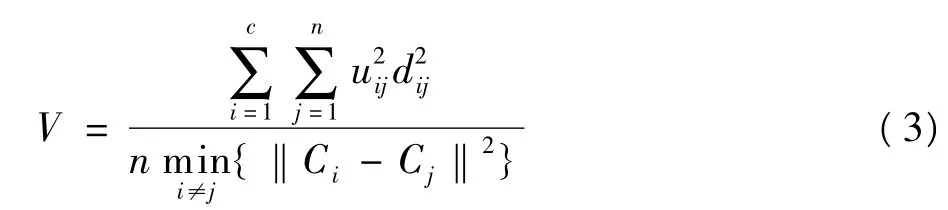
根据(3)式确定最优聚类数c*的步骤如下：①给定c的范围是［2，］〔12〕;②计算当时每个整数c对应的V值;③选取最小V值对应的c值，即为最优聚类数c*。

多尺度聚类模型及实例分析

1.多尺度聚类模型

对小脑组织的一组基因芯片数据，设基因芯片微阵列实验中，对小脑组织按照时间顺序进行了T次试验，每次试验所生成的芯片有N个基因，则可以得到N×T的基因表达矩阵。该模型的具体实施步骤为：

(1)对原始基因表达矩阵进行预处理;

(2)对每个基因在各个时间点所组成的信号作多尺度分解，记尺度数为K;

(3)将每个基因的第一尺度信号(记为aK)还原为基因表达数据，组成小脑组织N个基因在第一尺度的表达矩阵B1(N×T);同理，第m个尺度上的信号aK+dK+…+dK-m+1还原后组成N×T维的矩阵Bm(N×T)，由此我们得到了还原后的K个尺度的基因表达矩阵;

(5)基因归类：矩阵C的任意两行组成的向量表示任意两基因在m个尺度下的聚类结果。如果两向量相等即此时对应的二基因的聚类结果在各个尺度下完全一致，此时，我们认为可将此二基因归为一类，依次类推。

若基因A与基因B归为一类，基因B与基因C归为一类，但根据归类准则基因A与基因C不能归为一类，则此时基因B就同时归属于两类;而如果根据归类准则基因A与基因C也归为一类，那么此时基因A、B、C同时归属于一类。这样某些基因最后可能会同时归属于某几个类即最后的分类属于软划分，这样是符合生物学意义的。

因为最后归类时为一个取交集的思想，因此最后可能有某些基因不在任何分类中，会有缺失信息，因此多尺度聚类属于一个优化聚类。

(6)结合生物信息学相关知识对归类结果进行解释及评估。模型的具体实施步骤见图2。

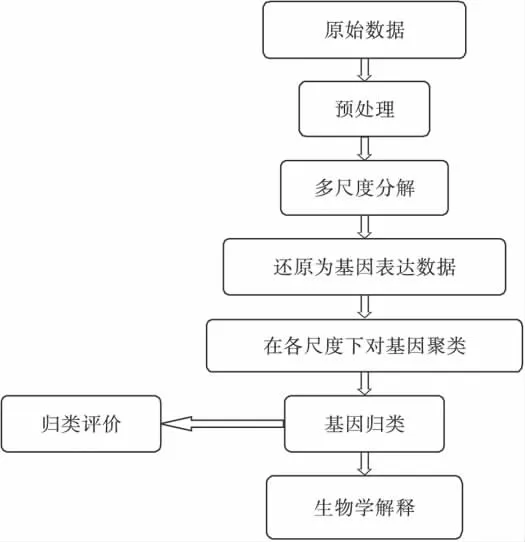
图2 多尺度聚类模型示意图

2.实例分析

(1)数据预处理

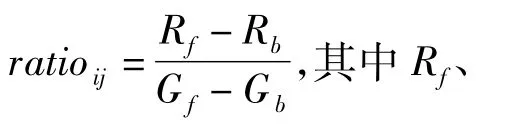
一般我们认为ratio'＞2或者ratio'＜0.5的基因是表达有显著变化的基因。一般情况下，当数值大于2时，我们认为基因上调;当数值小于0.5时下调。本文使用如下方法对原始基因表达数据xij按照如下步骤进行预处理：①在原始数据中去挑选出满足0＜xij＜0.5或者xij＞2的数据;②对挑选出的数据取以2为底的对数。通过对原始10080组数据进行预处理，最终得到了1068组有显著变化的基因表达数据，我们随机抽取其中100组连续有效数据作为实验(在不引起混淆的情况下，下文把这100组基因表达数据简称为基因数据)。

(2)多尺度分析结合FCM算法对小脑基因的聚类分析

本文首先对小脑基因进行多尺度分解及重构，小波基函数选择为Db5，尺度选为3层，第一尺度重构信号为a3，第二尺度重构信号为a3+d3，第三尺度重构信号为a3+d3+d2，此时得到的各尺度信号既可以有效表现出原始信号的大致概貌，又对峰值有很好的体现，且各尺度信号之间的一致性也表现的比较好。下使用上述多尺度聚类模型对各个尺度重构的基因表达数据进行模糊聚类分析，使用Matlab软件的模糊逻辑工具箱提供的函数，对于每个聚类数c(由Xie-Beni指数的求解步骤可知，c的取值范围在2～10之间)进行迭代，编写程序〔10〕进行模糊聚类，得出不同尺度不同的c值对应的Xie-Beni指数以及对应的聚类隶属度矩阵U=(uij)c×N。由此最后我们可以得出各尺度最优的聚类数均为c*=3，因此我们将这100个基因分为3类。在聚类过程中，3个尺度的方差分析结果均有P＜0.01，说明聚为3类能显著地将这100个7个时间点变量区分开。

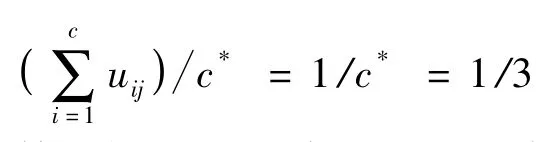
最后若某两个基因在各尺度下的分类结果完全一致，则最终归入到同一类，依此下去统计出最终的分类结果(见表1所示，这里我们只录入基因的实验标号)。

聚类结果分析及生物学解释

1.聚类结果的分类结果分析

从本文所得结果可以看出，将这100个基因分为3类是最优的聚类结果，类与类之间存在重复基因，如第43号基因同时归入第二类及第三类，45号基因同时归入第一类及第三类，这可能与某些基因的功能比较繁杂，参与生物学调控的方面比较多有关系，由文献〔13，14〕可知第43号基因KH-type splicing regulatary protein(KSRP)是一个参与了细胞发育中的多个过程的多领域RNA粘合蛋白质，而第45号基因myosin IC在细胞生长发育过程中参与了多个生物过程调控，与它们属于多分类相吻合;而这3类的基因的位置相对比较接近，即每个类中的基因成团分布在某几个块上。我们认为，在基因芯片的数据处理上，由聚类结果在基因芯片上的位置进行推测，在基因芯片制作的过程中，基因位置的选择或许有一定的规律，可能会将功能相似的基因放在一个块上，而且，位置越接近的基因实验条件越相近，其相互影响越大，从而在基因表达上有一定的同趋性。所以，从分类结果来看，我们认为是比较合理的。

表1 最终分类结果

2.聚类的生物学解释

数学模型推测出的分类结果是否合理，最好的方法是以实验方法去验证，而对于基因分类的结果好坏，最好的方法就是从生物学的角度进行解释，看所得结果是否符合生物学意义，类间的基因是否同质，这里的同质是指类间的基因是否在生物过程、细胞组成、分子功能这些方面有相似的地方。由于本课题研究的是胎儿发育过程中的小脑组织基因的调控规律，因此我们着重选择生物过程、发育过程、代谢过程、细胞构成、生物过程中的调控等项目，同时我们在基因类中只考虑具有调控功能的基因，并将类中所属的基因映射到Gene Bank(http：//www.ncbi.nlm.nih.gov/IEB/Research/Acembly)中查询其详细功能，代表性结论如下：

第一 类：例 如 No.22(as paraginyl-tRNA synthetase)、No.27(protein tyrosine phosphatase，receptort)、No.42(Lutheran blood group(Aubergerb antigen))、No.45(myosin IC)、No.58(phosphatidylinositol(4，5)bisphosphate)这5个基因都在细胞生长发育的过程起到了一定调控作用。如No.22(asparaginyl-tRNA synthetase)是一种Ⅱ型合成酶，它对细胞的生长发育起到明显的促进作用，在生物过程中起正调控作用;文献〔14〕显示No.45(myosin IC)与细胞生物合成及基因表达的转录过程有一定关联。

第二类：例如No.13(CLIP-associating protein 2)、No.19(single-stranded DNA binding proteinB)、No.33(guanine nucleotide binding protein)、No.43(KH-type splicing regulatary protein(KSRP))、No.53(hypothetical protein FLJ22638)这5个基因均属于组蛋白家族。

第三类：例如No.2(thyroid hormone receptor interactor 7)、No.3(transcription elongation factor B(SIII))、No.43(KH-type splicing regulatary protein(KSRP))、No.45(myosin IC)、No.67(polymyositis/scleroderma autoantigen 1)、No.89(chondroitin sulfate proteoglycan 6)这5个基因都参与了mRNA转录的过程，而其中No.43(KH-type splicing regulatary protein(KSRP))还属于组蛋白家族，因此也属于第二类;而No.45(myosin IC)还参与了生物过程调控，因此也属于第一类。

展望与建议

从聚类结果的分类结果及生物学意义分析来看，分类结果比较合理，符合FCM算法Xie-Beni指数最小以达到最优聚类，而分类结果的生物学解释也基本合理。结果表明该算法具有较高的准确性和稳定性，是一种有效的基因表达数据聚类方法，可以为进一步分析基因的生物学功能提供一个参考。

该模型的不足在于：(1)模糊隶属度的确定没有一个明确的准则以及结果的生物学解释还不够全面充实，我们从Gene Bank数据库只能查询某些基因的功能，不能查出基因之间的一些关系，因此结果的生物学验证不够充实和具体;(2)多尺度聚类为一个优化聚类，但是可能不能完全将所有个体归类，比如本例最终的聚类结果中少了1号及4号样本。如何能更加全面地考虑所有样本的信息是模型仍需改进的地方;(3)尺度数及小波基函数的确定尚没有统一理论指导，仍处于探索性阶段，做大量实验以及查阅大量文献做对比来验证优劣，如何找到一个适用的判别法则是我们今后工作的努力方向。

1.Futschik ME，Kasabov NK.Fuzzy clustering of gene expression data.IEEE Trans on Fuzzy System，2002(1)：414-419.

2.岳峰，孙亮，王宽全，等.基因表达数据的聚类分析研究进展.自动化学报，2008，34(2)：113-120.

3.文成林.多尺度动态建模理论及其应用.北京：科学出版社，2008：1-9.

4.潘泉，张磊，崔培玲，等.动态多尺度系统估计理论与应用.北京：科学出版社，2007：1-6.

5.Willsky AS.Multiresolution Markov models for signal and image processing.Proceedings of the IEEE，2002，90(8)：1396-1458.

6.普运伟，金炜东，朱明，等.核空间中的Xie-Beni指标及其性能.控制与决策，2007(7)：830-835.

7.樊启斌.小波分析及其应用.武汉：武汉大学出版社，2007：64-66，194-196.

8.李霖，吴凡.空间数据多尺度表达模型及其可视化.北京：科学出版社，2005：35-38.

9.刘青，邓庆山.基于有效性测度的基因表达数据的模糊聚类分析.计算机工程与科学，2005，27(9)：74-76.

10.Xie XL，Beni GA.A validity measure for fuzzy clustering algorithm.IEEE Trans on Pattern Anal Machine Intel，1991(8)：841-846.

11.宫改云，高新波，伍忠东.FCM聚类算法中模糊加权指数m的优选方法.模糊系统与数学，2005(1)：143-148.

12.于剑，程乾生.模糊聚类方法中的最佳聚类数的搜索范围.中国科学(E 辑)，2002(2)：274-280.

13.Hall MP，Huang S，Black DL.Differentiation-induced colocalization of the KH-type splicing regulatory protein with poly pyrimidine tract binding protein and the c-src pre-mRNA.Molecular biology of the cell，2004，15(2)：774-786.

14.Ivan CB，Edward DK.Localization of myosin IC and myosin II in Acanthamoeba castellaniiby indirect immunofluorescence and immunogold electron microscopy.The journal of cell biology，1990，111(5)：1895-1904.

Fuzzy Multiscale Clustering Analysis of Cerebella Gene Ex- pression Data

ChenJun，PanYan，TangShixing，etal．Depart-mentofMedicalStatistics，ThirdMilitaryMedicalUniversity(400038)，Chongqing

ObjectiveIn order to establish genetic classification in according with biological significance，and give reference to interpret some unknown gene’s function.MethodsFirst of all we did a multiscale analysis toward cerebella gene expression signal，subsequently we used an improved FCM clustering algorithm and design a classification threshold in various scales，then we used fuzzy clustering Xie-Beni index to achieve the optimal number of clusters and accomplish the clustering of cerebella genes of various scales，and each of class corresponding gene labelwas exported to txtfile，finally we found out the genes which were classified exactly the same in every layer and were conducted their biological explanations.ResultsThe optimal number of clusters of cerebella genes was 3 categories，and we according to the classification results comparison，we found thatmajority of genes in various types had close biological significance.ConclusionIt is effective to gene clustering where usemultiscale analysis combine FCM algorithm，the result has certain biological significance，it can give guidance in biological gene clustering and explaining gene function.

Multiscale analysis;FCM algorithm;Xie-Beni index;Clustering;Gene