对偶原理下的Menelaus定理与Ceva定理的统一
2011-02-02赵临龙安康学院数学系陕西安康725000
●赵临龙 (安康学院数学系 陕西安康 725000)
对偶原理下的Menelaus定理与Ceva定理的统一
●赵临龙 (安康学院数学系 陕西安康 725000)
在欧氏几何中,主要研究“三点共线”与“三线共点”问题的2个重要定理:梅内劳斯(Menelaus)定理和塞瓦(Ceva)定理.而在射影几何中,可利用对偶原理将梅内劳斯定理和塞瓦定理统一起来,充分揭示两者的本质联系.
1 Menelaus定理与Ceva定理
1.1 Menelaus定理
梅内劳斯作为一名古希腊的天文学家和数学家,关于圆中的弦撰写了6本论著.这些著作和梅内劳斯的许多其他著作都失传了.幸运的是梅内劳斯的3卷《球面几何》以阿拉伯文保存了下来,这部著作在希腊三角学的发展中起着重要的作用.第3卷展示了当时的球面三角学,著名的梅内劳斯定理作为本书的重要基础[1].
命题 1(Menelaus定理)[1]一直线与△ABC的3条边BC,CA,AB或延长线分别相交于点X,Y,Z,则

1.2 Ceva定理
塞瓦是意大利著名的经济学家、水利专家和几何学家,曾在重心计算法的研究上独树一帜,并取得了卓越的成就.他在研究各种图形的重心性质时,同时得到了直线性质,塞瓦定理正是在他本人所著的《直线论》一书中首先发表的[1].
命题2(Ceva定理)[1]在△ABC内任取一点O,直线 AO,BO,CO 分别交对边于点 X,Y,Z,则

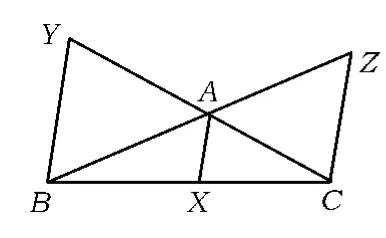
图1
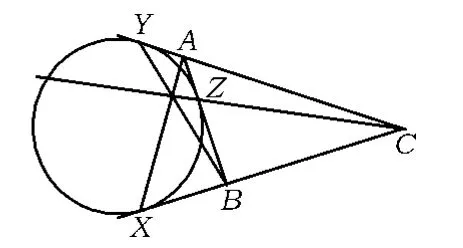
图2
2 Menelaus定理与Ceva定理的统一
在射影几何中,规定:平行线相交于无穷远(如通常的太阳“平行光”就是相交于无穷远点的“太阳”)[2].
在射影几何中,将一个命题的“点”换成“直线”,同时将“直线”换成“点”,并保持原有结构关系不变,所得到的新命题与原命题是“互为对偶命题”,并且2个互为对偶命题有“同真假”性质的对偶原理[2].
这样一来,可给出梅内劳斯定理和塞瓦定理相统一的结论——互为对偶命题.
命题3△ABC的3个顶点A,B,C与该三角形相对应的3条边BC,CA,AB所在直线各依次有点 X,Y,Z,则点 X,Y,Z 共线的充要条件是:
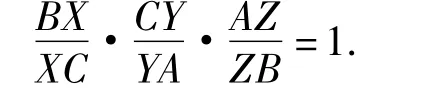
命题4△ABC的3条边BC,CA,AB所在直线与该三角形相对应的3个顶点A,B,C各依次有直线 AX,BY,CZ,则直线 AX,BY,CZ 共点的充要条件是:
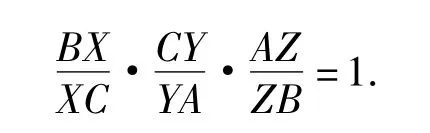
3 Menelaus定理与Ceva定理的推广
在射影几何中,还有另外2个研究“三点共线”与“三线共点”的定理互为对偶定理.
命题5(巴斯卡(Pascal)定理[3])一六角形ABCDEF内接于一条二次曲线Γ的充要条件是:这六边形3双对边AB与DE,BC与EF,CD与FA的交点共线.
命题 6(布列安双(Brianchon)定理[3])一六边形ABCDEF外切于一条二次曲线Γ的充要条件是:这六边形3双对角线AD,BE,CF共点.
特例(1)(命题5的退化形式)三边形内接一条二次曲线,则其3条边与对顶的切线的3个交点共线.
(2)(命题6的退化形式)三边形外切一条二次曲线,则其3个顶点与对边上的切点的3条连线共点.
3.1 定理的推广
命题7△ABC的一条外接二次曲线Γ在三顶点 A,B,C 的切线依次是 AX,BY,CZ,则该三角形的3条边BC,CA,AB与对顶切线3个交点X,Y,Z共线的充要条件是:
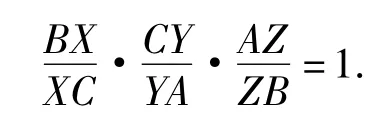
(梅内劳斯定理的推广)
命题8△ABC的一条二次曲线Γ在3条边BC,CA,AB 所在直线的切点依次是 X,Y,Z,则该三角形3个顶点A,B,C与对边切点3条连线 AX,BY,CZ共点的充要条件是:
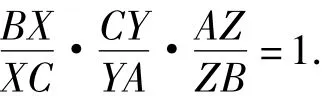
(塞瓦定理的推广)
2个命题只需要证明其中一个即可.如图2,对于命题8,由特例(2),得3条连线 AX,BY,CZ共点.又由塞瓦定理,得3条连线AX,BY,CZ共点的充要条件是:
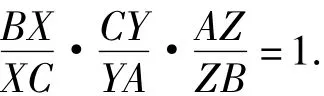
3.2 定理的变形
(1)在命题7中,当二次曲线Γ退化为圆时,是一道1989年新加坡数学竞赛题;在命题8中,当二次曲线Γ为椭圆时,是《数学学习》的“数学问题与解答”栏目中的问题 799[4].
(2)在命题7中,当二次曲线Γ退化为不在△ABC边上的一点时,就是塞瓦定理;在命题8中,当二次曲线Γ退化为不在△ABC顶点的一直线时,就是梅内劳斯定理.
结论(2)正好反映了梅内劳斯定理和塞瓦定理的内在联系,推广的梅内劳斯定理的退化是塞瓦定理;推广的塞瓦定理的退化是梅内劳斯定理.
(此文为陕西普通本科高等学校教学改革研究项目(09BY70);安康学院重点扶持学科《基础数学》建设项目(AZXZ0107).)
[1] 张红.数学简史[M].北京:科学出版社,2007.
[2] 朱德祥.高等几何[M].北京:高等教育出版社,1983.
[3] 赵临龙,张小文.射影几何中的共点线(共线点)定理的关系[J].鞍山师范学院学报,2003(3):44-46.
[4] 刘才华.数学问题与解答[J].数学学习,2009(12):46-47.
