高考创新题的命题走向及解题策略

●胡水林 (元济高级中学 浙江海盐 314300)

高考创新题的命题走向及解题策略

●胡水林 (元济高级中学 浙江海盐 314300)

《浙江省普通高考考试说明》中对创新意识能力的要求:能发现问题、提出问题，综合与灵活地应用所学的数学知识、思想方法，选择有效的方法和手段分析信息，进行独立的思考、探索和研究，提出解决问题的思路，创造性地解决问题．

在考试中创设新颖的问题情境，构造有一定深度和广度的数学问题，注重问题的多样化，体现思维的发散性．精心设计考查数学主体内容、体现数学素质的试题;反映数、形运动变化的试题;研究型、探索型、开放型的试题．

从2004年开始，全国16个省市独立高考命题，形成了“百花齐放”的局面．审视近几年的高考数学试题，不难发现:高考数学试题正经历着一个从“知识立意”到“问题立意”，再发展为以“能力立意”的过程，目的是突出考查学生的数学能力，并发掘学生的数学潜能，以符合新时代的人才要求．

创新题是近几年高考数学试题中备受青睐的一种题型．它多姿多彩的格调、清晰优美的风采、发散开放的形式、四两拨千金的巧妙，构成了高考试题中一道亮丽的风景线．如何引导学生立足于数学思想、数学系统，运用创新思维，“以子之矛攻子之盾”，从而突破层层表象的迷雾，抓住隐含的数学本质问题呢?仔细研究这些试题可以使我们明晰高考数学命题的动向和趋势，以帮助师生制定相应的解题策略，从而提高高三数学复习迎考的针对性和有效性．

1 以初等数学知识点为创新点命制试题

1．1以函数知识为背景

(2010年浙江省数学高考理科试题)

创意分析本题主要考查了函数的概念、定义域、值域、图像和对数函数的相关知识点，对数学素养有较高要求，体现了对能力的考查，属中档题．

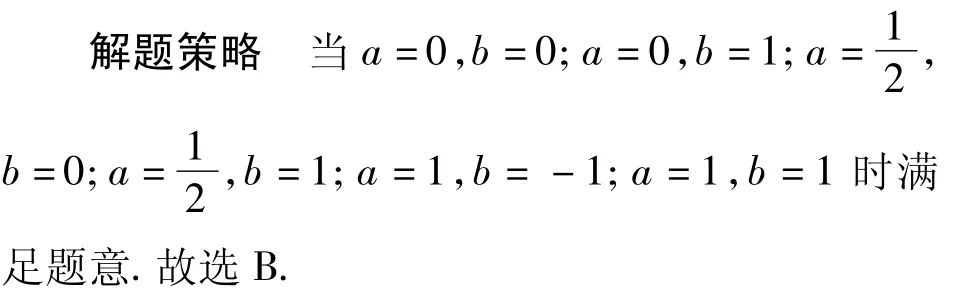
1．2 以数列定义为背景

创意分析本题以考生熟悉的等差、等比数列的定义为命题的出发点，创造性地构造“等差比数列”的新定义，在新定义下判断命题真假．这样命制体现了试题背景的公平性，考查了考生知识的迁移能力和应变能力．

解题策略透过新定义的表象，抓住问题的本质即等差、等比数列的概念，进行检验．答案选D．

1．3 以推递数列为背景

例3定义一种运算“*”:对于自然数满足以下运算性质:

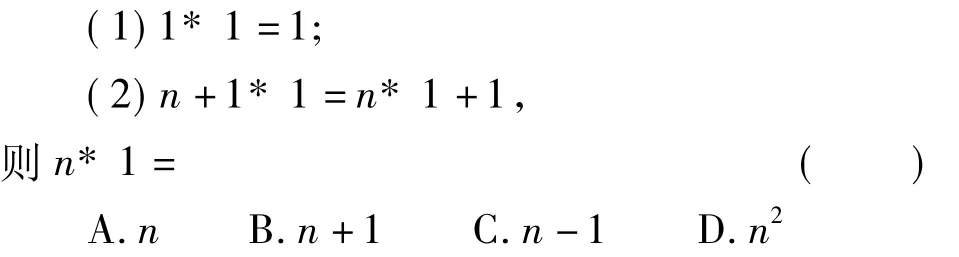
创意分析本题以规定了一种新的运算“*”形式命题，而本质以考生熟悉的递推数列为命题的出发点，考查学生的阅读能力和转化能力．

解题策略关健是要读懂题意，例如考生将“1*1”读懂为“a1”，将“n*1”读懂为“an”，则问题可转化为:已知 a1=1且 an+1=an+1，则an等于多少?即可知选D．

1．4 以直角坐标系为背景

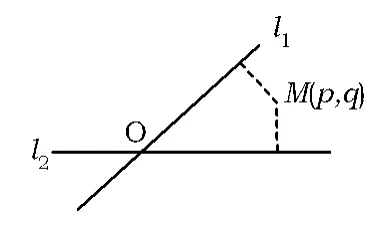
图1

例4如图1，平面中2条直线l1和l2相交于点O，对于平面上任意一点M，若p，q分别是点M到直线l1和l2的距离，则称有序非负实数对(p，q)是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题:

①若p=q=0，则“距离坐标”为(0，0)的点有且仅有1个;

②若 pq=0，且 p+q≠0，则“距离坐标”为(p，q)的点有且仅有2个;

③若pq≠0，则“距离坐标”为(p，q)的点有且仅有4个．

上述命题中，正确命题的个数是 ( )

A．0 B．1 C．2 D．3

(2006年上海市数学高考试题)

创意分析本题以学生熟悉的直角坐标系为母体，设计了“距离坐标”新定义，把一个动点到2条相关直线的距离所形成的有序非负实数对(p，q)定义为点的“距离坐标”，在新定义下判断几个命题的真假．这类创新题考查学生能否读懂题意，是否能将信息迁移．因而，这类创新题难度不大，但对阅读能力、理解能力、知识迁移能力、应变能力等要求相对较高．

解题策略①当p=q=0时，则点M只能落在直线l1和l2相交点O处，命题正确．

②当 pq=0，且 p+q≠0 时，例如 p=0，q≠0，则点M只能落在直线l1上，故只有2个点．

③若pq≠0时，点M可能落在直线l1和l2外，且到直线l1和l2的的距离分别是p，q，这样的点共有4个．

故选D．

1．5 以分段函数为背景

例5在实数的原有运算法则中，我们补充定义新运算“⊕”如下:当 a≥b时，a⊕b=a;当 a＜b时，a⊕b=b2，则函数 f(x)=(1⊕x)·x－ (2⊕x)(x∈［－2，2］)的最大值等于(“·”和“－”仍为通常的乘法和减法) ( )

A．－1 B．1 C．6 D．12

创意分析本题以考生熟悉的分段函数为命题的出发点，定义了一种新运算“⊕”．在这种新运算下，又有“·”和“－”通常的乘法和减法运算．这类创新题考查学生能否正确理解新运算的定义和新旧运算之间的混合运算的适应能力．

解题策略由题意得

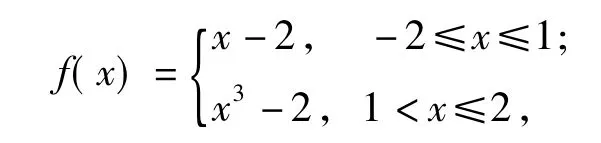
画图可知函数的最大值是6．故选C．

2 以新课程新增知识点为创新点命制试题

“坚持数学应用，考查应用意识”是近几年高考命题者坚持的一个命题方向，试卷突出新增加的如概率、导数等知识的应用性，反映出中学课程新增加的数学内容在解决实际问题中的重要作用．研究型、探索型、开放型试题是创新型试题的基本题型，有利于测试考生的能力与素质，有利于考查考生的探究精神．

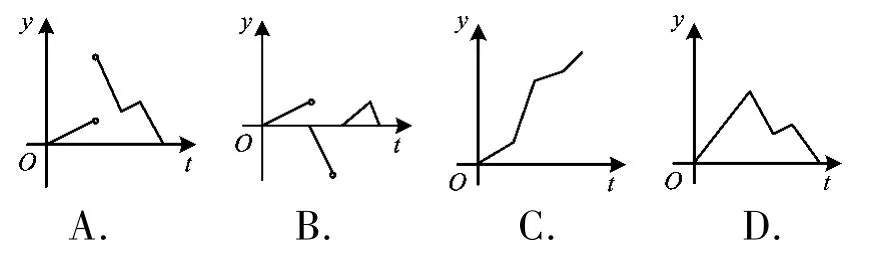
例6如图2，一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S(t)(S(0)=0)，则导函数y=S'(t)的图像大致为 ( )

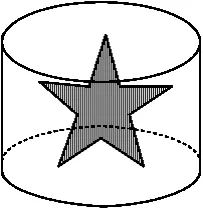
图2

(2010年江西省数学高考理科试题)

创意分析本题考查了阅读和理解能力，同时考查了学生对新知识、新事物的接受能力和加以简单运用的能力．既考查了应用意识，又考查了探究精神．要求解题者通过观察、阅读、归纳、探索进行迁移，即读懂和理解新情境，获取有用的新信息，然后运用这些有用的信息进一步推理，综合运用数学知识解决问题的能力和探索能力．

解题策略本题考查函数图像、导数图像、导数的实际意义等知识，最初零时刻和最后终点时刻没有变化，导数取0，因此排除选项C;总面积一直保持增加，没有负的改变量，排除选项B;考察选项A和D，差异在于两肩位置的改变是否平滑，考虑到导数的意义，判断此时面积改变为突变，产生中断，故选A．

3 以竞赛数学知识点为创新点命制试题

3．1 以函数迭代为背景

例7 若f(n)为n2+1(n∈N*)的各位数字之和，如:142+1=197，1+9+7=17，则 f(14)=17;记 f1(n)=f(n)，f2(n)=f(f1(n))，…，fk+1(n)=f(fn(n))，k∈ N*，则 f2008(8)=＿＿．

创意分析本题定义了一个新的函数f(n)为n2+1(n∈N*)的各位数字之和，以竞赛数学中的函数迭代定义fm(n)，从而求值．

3

．2 以格点(整点)为背景

创意分析本题以“格点”为背景，创造性地定义了“k阶格点函数”，而让学生判断哪些函数是“一阶格点函数”，让学生在读懂新定义情况下，判断哪些函数图像上有且只有一点横坐标、纵坐标均为整数．背景新颖，难度不大．

解题策略函数①只经过点(0，0)，函数②只经过点(1，3)，函数④只经过点(1，0)，而函数③经过点(0，1)，( －1，3)，( －2，9)，……．故答案是①②④．

3．3 以高斯函数背景

例9对于任意实数x，符号［x］表示x的整数部分，即是不超过x的最大整数，当x是整数时［x］就是x．函数f(x)=［x］叫做“高斯函数或取整函数”，则［log21］+［log22］+［log23］+［log24］+… +［log22 008］=＿＿ ．

创意分析本题给出“高斯函数”的定义，在高斯函数定义下求对数的值，关键是考查学生对x≤［x］＜x+1的理解和运用能力．

创意分析本题以“歌德巴赫曾研究过的问题”为背景，考查学生对极限思想与无穷项求和记号的理解，命制了让学生通过对题中“记号”进行观察、分析、归纳、总结，创造性地考查学生“研究性学习”的理念和方法．

4 以高等数学知识点为创新点命制试题

高等数学的一些基本思想、基本概念、基本方法为设计创新型试题提供了深刻的背景，这是因为高等数学的基本思想和方法是考查学生进一步学习潜能的良好素材．另外需要注意到，命题者大多数是大学教师，他们在命题时会受到自身学术兴趣和研究背景的影响．高考创新型试题一般都有比较深刻的高等数学背景，这类题目形式新颖，在课本例习题、复习资料和模拟试题中难以找到．

解答这类题目没有现成的方法可借鉴，会使一些考生感到难以人手，从而使该类题目有很好的区分度，因此命题教师十分青睐含有高等数学背景的试题．

4．1 以列行式为背景

4．2 以矩阵为背景

创意分析本题以“矩阵”为背景定义了新运算，并定义了运算的几何意义，其实质是考查学生初等数学中“映射”的概念，即:在平面上的点(x，y)在映射 f下变换成点(ax+by，cx+dy)．这样命制体现了试题背景的公平性，考查了学生对知识的迁移能力．

解题策略 由题意得

4．3 以狄利克雷函数为背景

创意分析本题设计了狄利克雷函数这个特殊函数，考查特殊函数的图像、极限、导函数和一次迭代等概念，明确点函数的图像、极限、导数等．

解题策略由题意得点函数的图像不是2条平行直线，当x→∞时的极限不存在，而f［f(x)］=1，故选 D．

4．4 以利普希茨条件为背景

例14定义:若存在常数k，使得对定义域D内的任意 2 个 x1，x2(x1≠x2)，均有

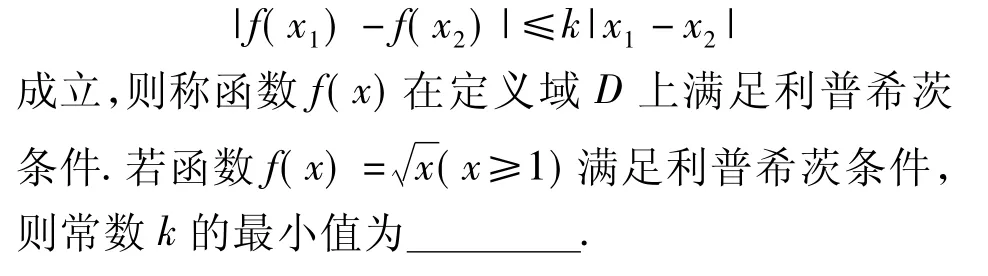
创意分析本题设计了定义“利普希茨条件”，考查学生对新知识的理解和运用能力．

解题策略由题意任意2个x1，x2(x1≠x2)∈［1，+∞)，得

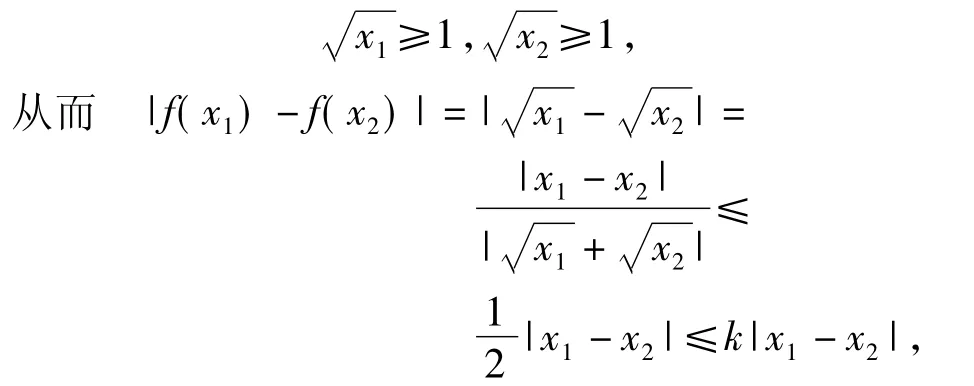
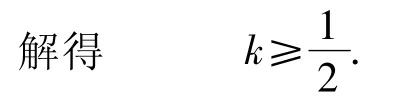
4．5 以微积分思想为背景

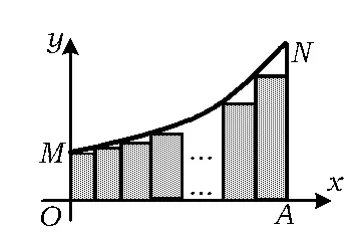
图3

例15曲线C:y=2x(0≤x≤2)两端分别为 M，N，且NA⊥x轴于点A．把线段 OA分成n等份，以每一段为边作矩形，使与x轴平行的边的一个端点在C上，另一端点在C的下方(如图3)．设这n个矩形的面积之和为Sn，则

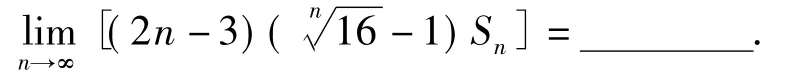
创意分析本题以高等数学中的微积分思想为背景，考查学生的等比数列求和公式、求极限的方法等．本题设计背景新颖、思想超前、难度适中．

解题策略将曲边梯形分割为n个矩形的面积之和Sn，而Sn又是等比数列的前n项的和，求出Sn，再求出所求极限，答案为24．

5 结束语

没有创新就没有发展;没有发展，事物就会失去存在的价值．在与时俱进的时代理念下，高考数学的创新发展势在必然．创新并不可怕，可怕的是面对创新题我们却无所作为．因此作为一线教师，作为学生学数学的领航员，必须做到以下几点:

(1)更新教学理念，激发有效课堂，注重通过多种形式与途径在课堂中培养学生的创新思维;

(2)要拓宽视域，研究高考创新题的题型、解法和走势，从中摸索到一些规律性的东西来指导创新数学教学;

(3)要关注生活，将生活引入数学课堂，让数学课堂关注生活问题，通过暗示、诱导、逆向启发等多种手段训练并培养学生运用数学知识解决生活问题的思维与能力;

(4)要学生创新，教师得先创新，要努力学习新课程理念，探索新课程标准下的数学创新教学的有效途径，争创一个能解会编、能教会导创新题的身体力行的创新型教师．