从竞赛到高考的装错信笺题及变式题探究

●甘大旺 (北仑明港中学 浙江宁波 315806)

从竞赛到高考的装错信笺题及变式题探究

●甘大旺 (北仑明港中学 浙江宁波 315806)

瑞士数学家伯努利提出了装错信笺问题——某人写了n(n∈N+)封不同的信，并在n个信封上写下对应的地址，问:把所有信笺全部装错的方法共有多少种?

后来，著名数学家欧拉认为此题是“组合理论的一道妙题”，并运用递推数列{xn}独立地解决了这道妙题，求出的方法种数用阶乘表示为

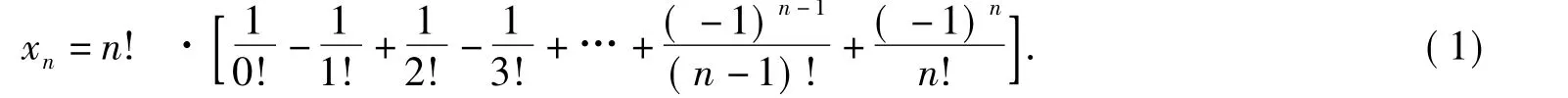
欧拉解法的关键是找出递推数列的递推式xn+2=(n－1)(xn+1+xn)，难点是后续的求通项．下面笔者另辟蹊径，运用容斥原理验证式(1)．

证明当正整数n≥2时，将这n封信笺任意装入这n个信封，不管装对装错，共有n!种方法．其中，至少有1封信笺恰好正确装入信封的任意装法有·(n－1)!种;至少有2封信笺恰好正确装入信封的任意装法有·(n－2)!种;至少有3封信笺恰好正确装入信封的任意装法共有·(n－3)!种;…;至少有n－1封信笺恰好正确装入信封的装法共有·1!种，因此所有n封信笺都正确装入信封的装法共有种．根据容斥原理知，符合题意的投放信笺方法种数共有

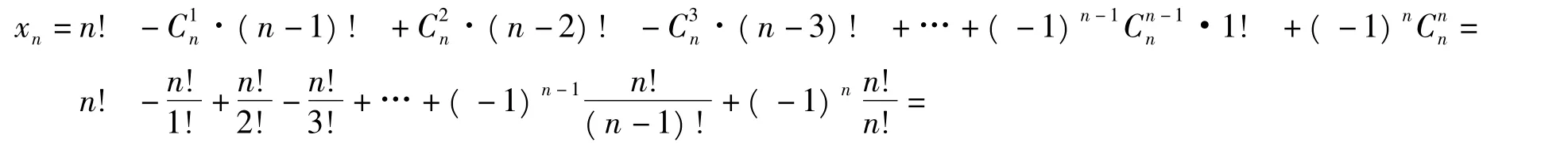
伯努利—欧拉装错信笺的经典问题，有时呈现特例、有时变换情景、有时变换目标，活跃在数学竞赛题和高考题中．对于这类直白或翻新的经典问题，假如能自觉运用上述结论(2)，就可以轻松、快捷、愉悦地解决，并培养模式识别、等价变换的数学思想．

例1某人给6个不同的收信人写了6封信，并且分别写好了6个信封，问有多少种投放信笺方法使得信笺和收信人皆不相符?

(1960－1961年波兰数学竞赛试题)

解在伯努利—欧拉装错信笺问题中，取n=6，直接运用结论可知，共有种投放信笺方法，使得信笺和收信人皆不相符．

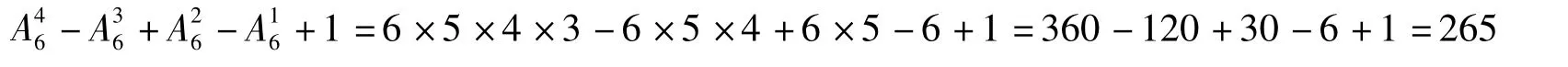
评注此题是伯努利—欧拉装错信笺问题当n=6时的特例，沿用了经典问题的情景．

例2将数字1，2，3，4填入标号为1，2，3，4的4个方格里，每格填1个数字，则每个方格的标号与所填的数字均不相同的填法有＿ 种．

(1993年全国数学高考试题)

解对应于伯努利—欧拉装错信笺问题，取n=4，则每个方格的标号与所填的数字均不相同的填法有－+1=12－4+1=9种．

评注此题变换了伯努利—欧拉装错信笺问题的情境，数字1，2，3，4对应着信笺，标号为1，2，3，4的4个方格对应着信封．

例34封不同信件放入4只写好地址的信封中，全装错的概率为 ．

(2005年上海交通大学自主招生试题)

解4封不同信件放入4只写好地址的信封中，任意放入的方法共有4!种，其中全装错的方法有－+1种，因此全装错的概率为

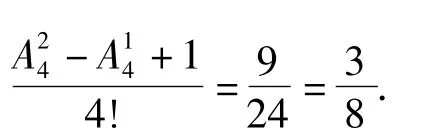
评注此题保持了伯努利——欧拉装错信笺问题的情境，但把解题目标变换为求概率．

例4把5枚无区别的棋子放在5×5小方格中(如图1)，每行每列放且仅放1枚棋子，不允许放在黑色小方格内，则共有＿＿ 种放法．

(2006年浙江省数学竞赛试题)

图1

图2

解第1步，先构造如图2所示的5×5小方格，其中把第 k行第 k列(k=1，2，3，4，5)的小方格染成黑色，现在把5枚无区别的棋子放在这个新5×5小方格中，每行每列放且仅放1枚棋子，不允许放在黑色小方格内(即第k行第k列不放棋子)，这与伯努利—欧拉装错信笺问题当n=5时的情形同构，此时有－+－1种放棋子方法．

第2步，将上述构造的5×5小方格的第1列与第2列全部对调、第4列与第5列全部对调，就回归了题意，此时只有1种固定的方法．

根据乘法原理可得，符合题意的放法种数共有

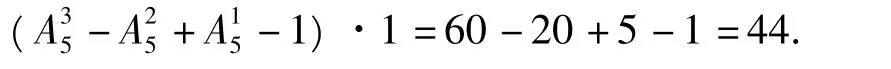
评注一般地，设 A={a1，a2，a3，…，an}，{b1，b2，b3，…，bm}，其中正整数 n≥2，根据集合中元素的无序性可能交换B中元素的位置，可得B={bk1，bk2，bk3，…bkn}．在由A到B的一一映射f:A→B中，若不允许所有的am与akm(m=1，2，3，…，n)相对应，则这种一一映射的个数共有

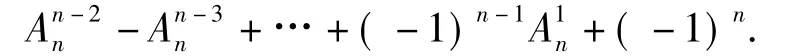
例5某人有3种颜色的灯泡(每种颜色的灯泡足够多)，要在如图3所示的6个点A，B，C，A1，B1，C1上各安装一个灯泡，要求同一条线段2端的灯泡不同色，则不同的安装方法共有＿＿ 种．

(2008年重庆市数学高考文科试题)

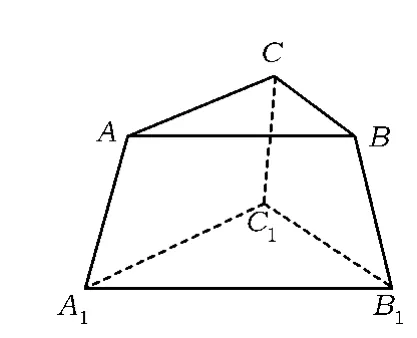
图3

解第1步，在A，B，C处各安装一个灯泡，要求用到3种颜色的灯泡各1个，有种方法;

第2步，在A1，B1，C1处各安装一个灯泡，也用到上述3种颜色的灯泡各1个，还要求A与A1，B与B1，C与C1处的灯泡都不同色，这与伯努利—欧拉装错信笺问题当n=3时同构，此时有－1种安装方法．

评注这道高考题的情景设置贴近实际，与2008年全国数学高考文科试题Ⅰ第12题有异曲同工之妙．解答过程中第2步的本质与伯努利—欧拉装错信笺问题相吻合．

例6有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”5个项目的测试，每位同学上、下午各测试一个项目，且不重复．若上午不测“握力”项目，下午不测“台阶”项目，其余项目上、下午都各测试一人，则不同的安排方法共有 种(用数字作答)．

(2010年浙江省数学高考试题)

解为方便叙述，把题设的4位同学分别记为甲、乙、丙、丁，把“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”等5 个项目依次记为 A，B，C，D，d．依题意，上午安排 A，B，C，d 各一项，下午安排 A，B，C，D各一项，且同一人的上、下午不能同测．

第1步，给甲、乙、丙、丁安排上午的A，B，C，d项目，此时有种方法．

第2步，给上午测试、项目的同学安排下午的测试项目，分2小类:

(1)当D与d安排给同一人时，下午的A，B，C项目不能与上午的此项目安排给同一人，这与伯努利—欧拉装错信笺问题当n=3时的情形同构，此时有－1种方法;

(2)当D与d不安排给同一人时，把与d视为同类，把A，B，C与自身视为同类，则下午的A，B，C，D不能与上午的同类项目安排给同一人，这与伯努利—欧拉装错信笺问题当n=4时的情形同构，此时有－+1种方法．

根据乘法原理和加法原理，得不同的安排方法共有

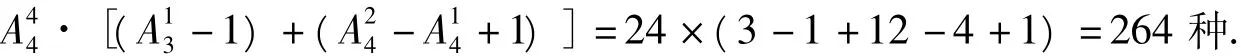
评注这里运用伯努利—欧拉装错信笺问题解题，有2点创新:一是局部运用此经典问题;二是把此经典问题中的相同元素不重复情形恰当拓宽为同类元素不重复．

综上所述，伯努利—欧拉装错信笺问题较早出现在竞赛题中，随后活跃在数学高考题和竞赛题中．由此看来，探究在数学高考大纲与数学竞赛大纲公共范围内的竞赛题，是高考数学的命题研究、解题研究的新途径．

［1］ 郑国荣．高中生数学辞海［M］．上海:上海人民出版社，2001．

［2］ 芮玉贵．模式识别解题的理论探讨［J］．数学通报，2010(3):45-47．