LMS类算法在磁轴承滤波补偿中的应用分析

高 辉 徐龙祥

南京航空航天大学，南京，210016

LMS类算法在磁轴承滤波补偿中的应用分析

高 辉 徐龙祥

南京航空航天大学，南京，210016

主动磁悬浮轴承（AMB）系统中存在与转子同频的时变不平衡干扰信号，此信号会影响系统的控制效果。为了滤除这些不平衡信号，通过分析几类最小均方（LMS）误差算法，得出一种相对合适的滤波算法。根据AMB系统中干扰信号的幅值以及频率实时变化情况，对原算法进行了改进，并比较了改进算法与原变步长算法对时变信号的滤波效果。仿真与实验结果显示，改进算法对时变的幅值较小信号具有更好的跟随期望信号能力及收敛能力，为主动磁悬浮轴承系统的实时滤波补偿提供方便。

主动磁悬浮轴承（AMB）；频率不等；变步长LMS算法；频率时变性；自适应滤波

0 引言

主动磁悬浮轴承（AMB）系统因具有无接触、无摩擦、无污染、高效率、低能耗、主动控制等优点而被广泛应用于工业及国防领域［1］。但是与普通旋转装置一样，由于转子质量不均匀，AMB系统工作时也存在与转子同频的时变不平衡干扰影响，此影响将不仅增加系统基础的振动响应，增大噪声干扰，同时还降低系统控制稳定性。针对此影响的一种抑制方法被称为惯性力最小补偿方法［2－5］，即力自动平衡方法，该方法通过滤除转子反馈位移信号中与转速同频的正弦不平衡信号而使转子绕其惯性轴旋转，从而减小不平衡力通过径向轴承对基础的振动，增加系统的控制稳定性。

LMS类算法作为一种自适应滤波算法在许多领域得到广泛应用，在AMB领域也有应用，如文献［3－5］采用标准LMS算法进行自适应滤波处理，但由于标准LMS算法固定步长因子与收敛速度和稳态误差之间存在矛盾，因此文献［3－5］仅仅是在定转速处分析了LMS算法在AMB系统中的滤波效果。由于AMB系统现场工作时因转子频率的变化而产生与转子同频的时变不平衡干扰信号，因此文献［3－5］中的方法不能减小该时变信号对系统的影响。

本文通过分析标准LMS算法及几种变步长LMS算法在AMB系统中的应用情况，得到一种相对合适的变步长算法并将其作为自适应滤波补偿器。针对转子反馈位移误差信号幅值较小的特点对原算法进行了改进，目的是提高AMB系统的控制稳定性和收敛速度。同时，考虑到转子转速频率的时变性，为了对时变转子信号进行实时滤波补偿，在改进算法基础上又提出一种新的改进算法，此算法可根据转速的变化对转子周期性位移信号进行实时有效滤波。

1 原LMS类算法在AMB中应用分析

LMS类算法的精髓就是利用梯度随机下降原理实现目标函数的最小化，即迭代时算法中权矢量沿误差性能曲面梯度估值的负向按给定比例更新［6］，因此权矢量的迭代过程是研究LMS类算法的关键。图1为LMS类算法的工作原理图。其中，d（k）为期望信号，y（k）为算法输出信号，e（k）为误差信号，W（k）为权向量，X（k）为算法输入向量，μ（k）为可变步长因子，以上变量都是表示离散系统中k时刻的相应值。

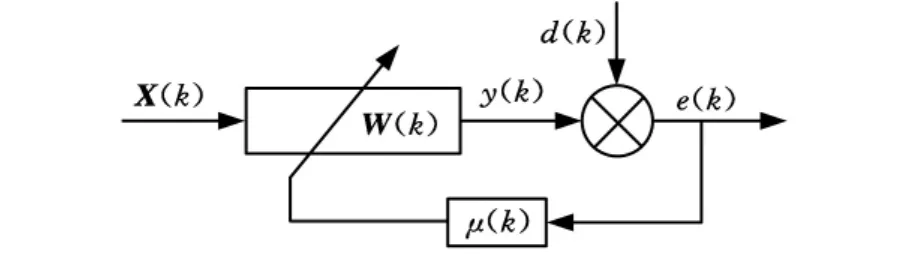
图1 LMS类算法原理

任何LMS类算法的核心均表现为权矢量的迭代更新过程，有如下公式描述：

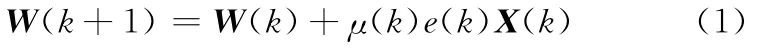
其中，X（k）为给定信号，所以权矢量的更新主要依靠误差信号e（k）以及可变步长因子μ（k）的变化，可依据误差信号的变化特性来评价LMS算法优劣，即依据式（1）的迭代保证y（k）跟随d（k），从而使e（k）最小，其表达式如下：

依据式（1）、式（2）可最终实现自适应滤波，因此分析各种LMS算法的关键在于分析其步长因子。

1.1 标准LMS算法的不足

如果式（1）中的μ（k）为常数，则其为标准LMS算法，即μ（k）＝μ。针对文献［3-5］仅仅在固定频率处进行滤波分析，可从算法固定步长因子μ与输入信号频率ω0对算法滤波品质因素的影响及算法均方误差等方面进行分析。

因此可推知在确定品质因素条件下，算法中一个确定的固定步长仅对应一个较小的输入信号频带。

下面给出标准LMS算法均方误差公式［8］：

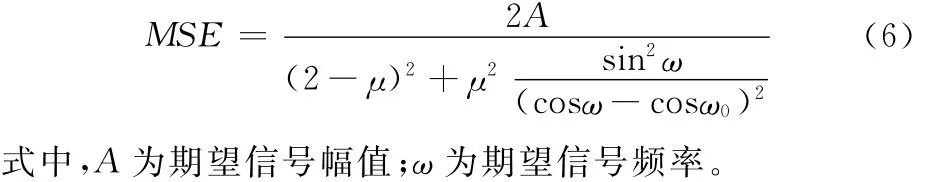
当ω0＝ω时，MSE＝0；当ω0≠ω时，从式（6）可知，MSE为一个不等于0的常数，从而影响滤波效果。现取相同固定步长因子μ＝0.08，输入信号频率f0＝400Hz，期望信号频率f分别为400Hz、380Hz（这里ω＝2πf），来验证式（6）的正确性，MSE与输入信号频率及期望信号频率关系如图2所示。

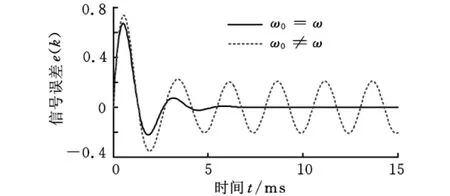
图2 MSE与输入信号频率及期望信号频率关系

由图2可知：当输入信号频率与期望信号频率相等时，误差响应信号大约两个周期后达到最小，即能够有效滤波；当二者频率不等时，误差信号的稳态响应为一正弦波动，即滤波不彻底。以上分析中，输入信号频率为事先给定的固定值，因此在AMB系统应用中，标准LMS算法只能实现对定转速滤波补偿，并且由式（5）可推知每个固定的步长因子仅适用于一个较小的转速频带。为了满足AMB系统的实际工业应用，针对周期性振动响应需要对系统进行实时滤波补偿控制的问题，考虑应用变步长LMS算法。

1.2 变步长LMS类算法分析

根据需要列出三类可变步长LMS算法。文献［9-10］中提出一种变步长LMS算法，简称CP－LMS算法，其可变步长因子为

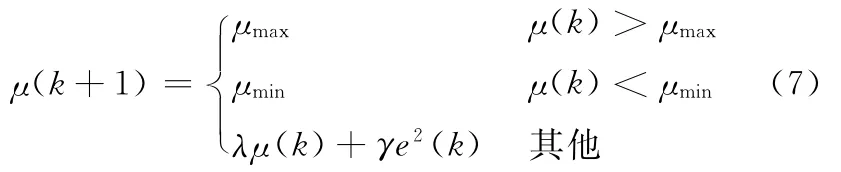
式（7）中的可变步长因子在最大给定值μmax以及最小给定值μmin之间变化，同时由前一次的可变步长因子和误差信号决定。此算法需要同时确定合适的μmax、μmin、λ 以及γ 四个参数才能有效滤波。

文献［11-12］提出的SVSLMS算法中，其可变步长因子为

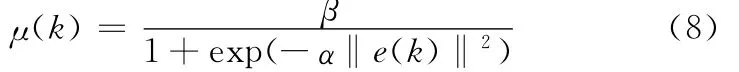
式（8）中的误差信号在exp幂函数作用下改变步长因子取值，同时匹配合适的β以及α两个参数。

在文献［13-14］等提出的MNVSS算法中，其步长因子为

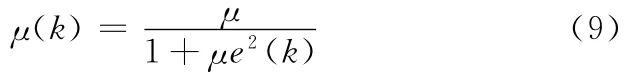
式（9）中可变步长因子仅与误差信号和固定步长因子μ有关。

考虑到AMB系统反馈位移信号幅值可变性，现提供一幅值突变正弦信号作为期望信号，前15ms时幅值为1.0，随后幅值变为0.6。选取μmax＝0.06，μmin＝ 0.0006，λ ＝ 1.0，γ ＝ 0.0008，β＝0.06，α＝5，μ＝0.06。利用 CP－LMS、SVSLMS和NVSS三种算法对给定期望信号进行滤波仿真，图3给出了三种算法的滤波效果（可变期望信号在图中未显示）。

从图3可以看出，当主参数μmax、β、μ取值相同时，期望信号变化前后仅有NVSS算法收敛性最好。同时，考虑到AMB系统的强耦合性、非线性以及控制系统参数复杂性，依据自适应滤波算法可变参数越少越好原则，本文认为NVSS类算法更适合用在AMB滤波补偿控制中。

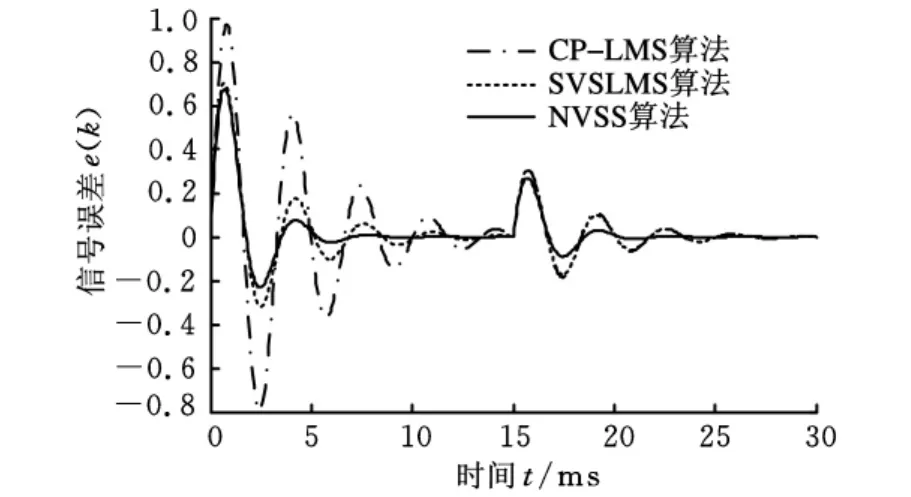
图3 三种LMS算法误差信号收敛曲线

1.3 NVSS类算法分析

文献［13］中给出MNLMS算法可变变步长因子的表达式为

式（10）中可变步长因子是算法输入信号范数平方的非线性函数。与文献［13］不同，式（11）中可变步长因子是误差信号范数平方的函数。但是式（10）、式（11）都是对相应信号平方的累加作为影响可变步长因子变化的因素，会增加运算量，并且当外界期望信号变化时式（11）、式（12）两种算法再次收敛的灵敏度不高。因此文献［14］给出NVSS算法的改进算法，即式（9）中的MNVSS算法。式（9）中用e2（k）代替式（11）中的 ‖e（k）‖2，使μ（k）的变化仅取决于当次迭代运算中的误差信号的平方。MNVSS算法解决了运算量大的缺点并且可以保证变化的期望信号重新快速收敛。图4给出了MNVSS类算法在三种不同的可变步长因子时对幅值变化信号的滤波效果对比。其中期望信号均是前半部分幅值为1、后半部分幅值为1.2、频率为400Hz的正弦信号（图4中未显示），三个步长因子中有相同的μ值，均为0.08。由图4分析可知，当期望信号幅值发生变化时，只有MNVSS算法的误差信号可以很好地再收敛，因此针对AMB系统中幅值及频率时变的位移反馈信号的实时滤波，可考虑应用MNVSS算法。

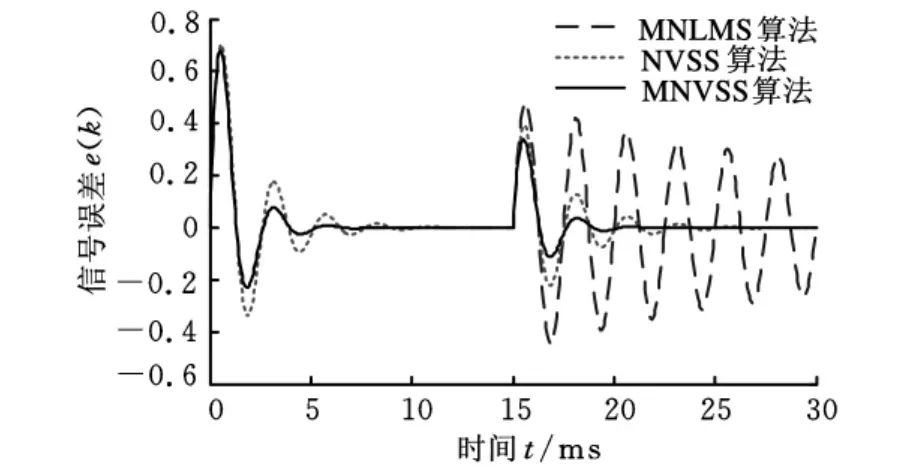
图4 MNVSS类算法在不同步长因子时的误差信号比较

2 MNVSS算法在AMB系统应用中的改进

2.1 定转速时滤波算法改进

考虑到AMB系统中位移电压信号的幅值较小的特点（一般情况下的幅值都小于1.0，在转子正常旋转时，一般转动频率为500Hz，其幅值小于0.6），由式（2）、式（9）知，MNVSS算法在运算过程中有最大误差信号emax（k），并且emax（k）＜dmax（k）＜ 1.0，所以存 在 不 等 式e2max（k）＜emax（k）。现对式（9）进行变形处理，有

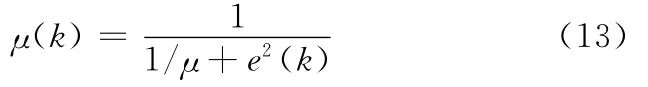
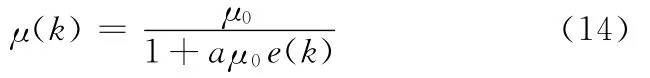
其中，μ0为参考步长因子，针对不同频率的期望信号，事先要选择合适的μ0值，一般μ0取值的数量级为10－2；a为加权系数，起放大作用，目的为增加误差信号在可变步长因子中的影响，其实际取值可参考期望信号的幅值情况，一般为20～30。

在式（14）中用ae（k）代替式（9）中的e2（k），即可变步长因子仅是误差信号的非线性函数，其目的是为了增加误差信号对可变步长因子的影响程度。

现选择幅值为0.6、频率为200Hz的正弦信号作为期望信号，取a＝20，μ0＝0.04，对 MNVSS算法及M－MNVSS算法的误差信号进行比较，如图5所示。

从图5可看出，两算法都有很快的收敛速度，误差信号在经过一个周期后基本重合，两个周期后两误差信号趋于零，但是M－MNVSS算法误差信号跟随期望信号的能力明显好于MNVSS

此时，当e（k）变化时，因为1／μ≫1［14］，式（13）中的μ（k）受e2（k）的影响较小，则在AMB系统不平衡滤波补偿中达不到最理想控制效果。

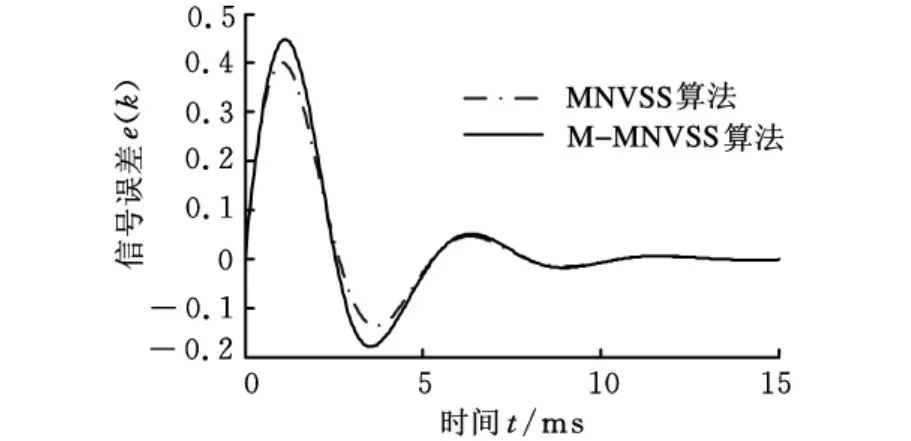
图5 算法误差信号比较

现参考MNVSS算法提出一种针对AMB系统不平衡滤波补偿的改进的变步长算法，称之为M－MNVSS算法，其可变步长因子为算法。因为磁悬浮轴承系统具有主动控制周期短、转动频率高等特点，当此误差信号作为功率放大器输入时，只有其能够更好地响应转子反馈位移信号，即跟随期望信号，才能在实施滤波时更有利于提高系统控制稳定性。

式（14）中的可变步长因子在滤波处理过程中虽然同时具有好的跟随期望信号能力和较快的收敛速度，但是当参数μ0确定后，M－MNVSS算法也只能对一固定频带有好的滤波效果，当期望信号频率变化相对较大时，其对期望信号跟随能力明显降低，如图6所示。对于相同的μ0，取值为0.08，当f＝400Hz时，从误差信号特性曲线上分析知其有好的滤波效果，当f＝200Hz时，其跟随期望信号能力明显降低。因此在AMB系统实时变速滤波补偿控制时，如果将其作为控制器输入信号对系统进行实时控制，由于误差信号对转子位移反馈信号的跟随灵敏度减弱而降低控制系统稳定性，就会导致系统失稳，影响AMB系统的正常工作。

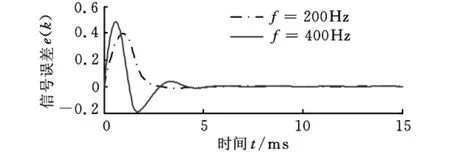
图6 M－MNVSS算法对不同频率信号的误差特性曲线

2.2 实时旋转时滤波算法改进

经过上述分析，自适应滤波算法在AMB系统实时滤波补偿控制应用中应具有以下特点：

（1）既要有好的跟随期望信号能力，以免控制系统在转速变化时失稳，又要有较快的收敛速度，以达到比较理想的滤波效果。

（2）算法应具有简单的结构以便节约运算时间，有利于实时控制，因为系统要求有很小的控制周期；算法可调参数尽量少，方便联合调试。

（3）算法应能很好地跟踪转子位移信号的转动频率，以便实现变转速实时滤波补偿。

针对以上特点以及式（5）中的要求，本文提出一种新的改进算法，简称NM－MNVSS算法。此算法中可变步长因子为

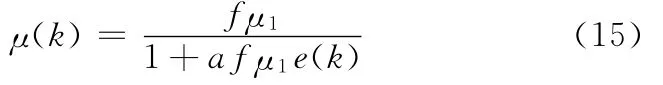
其中，期望信号频率f在这里为实时检测到的AMB系统转子转动频率（Hz），期望信号d（t）的角频率ω＝2πf；μ1是个很小的正参数，此值可根据式（5）及f的范围选取，一般μ1取值的数量级为10－4。由式（15）知，当a 、μ1确定后，μ（k）主要依据转动频率f和误差信号e（k）而变化。

图7给出NM－MNVSS算法在相同参数情况下针对不同频率时的滤波效果，其中a＝20，μ1＝0.0002，可以看出，当f 分别为400Hz、200Hz时新算法都有很好的滤波效果，既能很好地跟随期望信号又能快速收敛。图8给出MMNVSS算法及NM－MNVSS算法在期望信号频率实时变化时的误差响应比较。15ms前期望信号是幅值为0.6、频率为200Hz的正弦信号，15ms后期望信号幅值突变为0.4，频率变为400Hz。从图8分析得出，在频率为200Hz时两种改进算法有相同的收敛能力，但是当频率突变时，NM－MNVSS算法能很好地再次跟随期望信号并很快实现信号对消，而M－MNVSS算法虽然跟随能力比较好但其收敛速度明显变慢。因此可初步验证NM－MNVSS算法在AMB系统中对频率时变的转子位移反馈正弦信号能够实现有效滤波，并使系统控制环节在变频滤波控制时保持稳定悬浮控制。

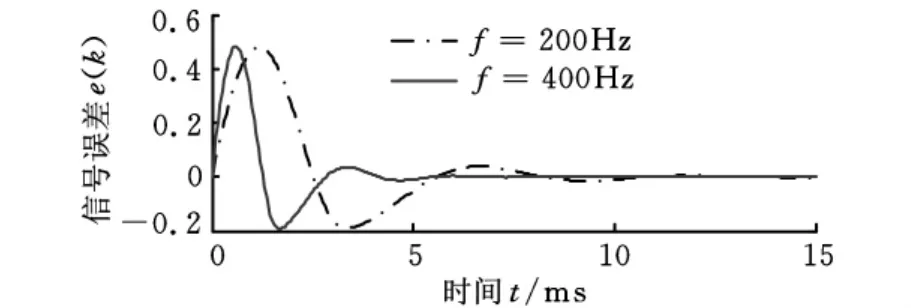
7 NM－MNVSS算法对不同频率信号的误差特性曲线

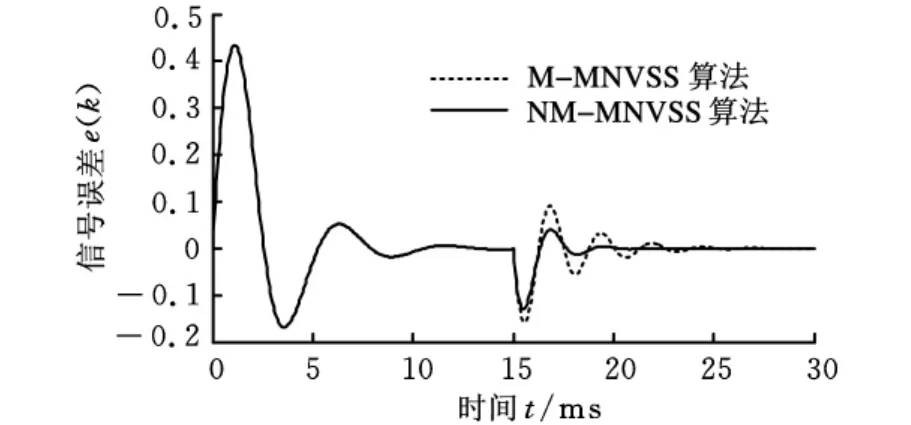
图8 变频、变幅值时两改进算法的滤波效果比较

3 实验

针对AMB系统中转子位移反馈信号的滤波处理，所设计的滤波控制系统框图见图9。

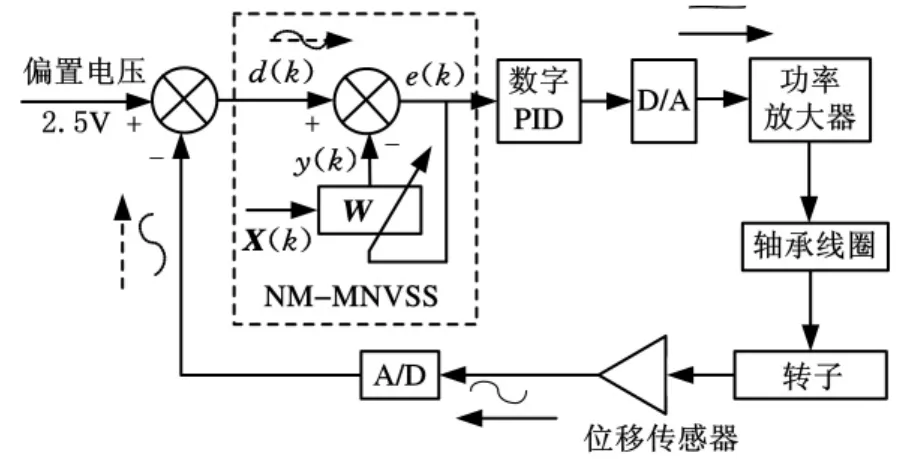
图9 加滤波算法后AMB控制系统

在数字PID控制器前串联NM－MNVSS算法作为自适应滤波器，使算法经过迭代运算后实现对信号的滤波对消，以便减小功率放大器输入端的位移电压幅值，从而降低不平衡力对系统基础振动响应，提高控制稳定性。图10为AMB系统的实验装置图，其中，补偿控制算法由PC机完成，DSP2407芯片实现数字采样以及转速测量，PCI卡实现PC机与DSP之间的数据交互，变频器的作用是驱动电机使转子转动，转接箱的作用是方便AMB系统联合调试，转子的径向位移信号以及控制电流信号由示波器显示。

图10 AMB实验装置

现对转子频率为200Hz时的AMB系统进行滤波补偿，选取μ1＝0.0002，PID主要参数为Kp＝0.875，Ti＝0.545，Td＝0.679，利用这些参数进行旋转实验。通过分析可知，200Hz时滤波补偿后的控制电流曲线基本趋于一条直线，说明NM－MNVSS算法的滤波效果比较明显。然后在μ1相同的前提下对400Hz时的系统进行滤波补偿，此时的PID参数分别为Kp＝1.025，Ti＝0.545，Td＝0.569。同样可得出400Hz时补偿前后的电流曲线趋于平直，说明NM－MNVSS算法也有很好的滤波效果。

上述分析说明了新改进算法NM－MNVSS对不同频率、不同幅值的正弦信号都有比较理想的滤波效果，进一步验证了图8所示结论的正确性。但可以看出在200Hz和400Hz时对应的PID控制参数不同的，从侧面说明如果要实施实时在线滤波补偿，需要采用合适的控制器以及合理的控制策略。

4 结束语

本文针对AMB系统中转子反馈正弦位移信号的小振幅现象及频率的时变性，提出一种对此类变化的期望信号进行滤波对消的新的变步长LMS算法（MN－MNVSS），并通过不同定转速补偿实验验证了NM－MNVSS算法在AMB系统滤波补偿应用中的有效性。NM－MNVSS算法的提出为AMB系统实时滤波补偿提供一种可行性参考。

［1］ Betschon F，Schob R.On－line－adapted Vibration Control［C］／／Proceedings of the Sixth International Symposium on Magnetic Bearings.Mito，Japan，1998：362－371.

［2］ 黄晓蔚，唐钟麟.电磁轴承系统实现自动平衡的一种新方法［J］.机械工程学报，2001，37（7）：96－99.

［3］ Shi J，Zmood R.The Direct Method for Adaptive Feed－forward Vibration Control of Magnetic Bearing Systems［C］／／7th International Conference，Control，Automation，Robotics and Vision.Singapore，2002：675－680.

［4］ Vahedforough E，Shafai B，Beale S.Estimation and Rejection of Unknown Sinusoidal Disturbances Using a Generalized Adaptive Forced Balancing Method［C］／／Proceedings of the American Control Conference，2007’ACC.New York，2007：3529－3534.

［5］ 高辉，徐龙祥.基于LMS算法的磁悬浮轴承系统振动补偿［J］.振动工程学报，2009，22（6）：583－588.

［6］ Feuer A，Weinstein E.Convergence Analysis of LMS Filters with Uncorrelated Gaussian Data［J］.IEEE Trans.Acoust.，Speech，Signal Process，1985，33（1）：222－229.

［7］ Vaz C，Kong X，Thako N.An Adaptive Estimation of Periodic Signals Using a Fourier Linear Combiner［J］.IEEE Transactions on Signal Processing，1994，42（1）：1－10.

［8］ Xiao Y，Tadokoro Y.LMS－based Notch Filter for the Estimation of Sinusoidal Signals in Noise［J］.Signal Processing，1995，46（2）：223－31.

［9］ Woo J S，Min S P.A Complementary Pair LMS Algorithm for Adaptive Filtering［C］／／Acoustics，Speech，and Signal Processing.Munich，1997：2261－2264.

［10］ Yue W，Chun Z.A New Variable Step Size LMS Algorithm with Application to Active Noise Control［C］／／ Proceedings of International Conference on Acoustics，Speech and Signal Processing.Hong Kong，2003：573－575.

［11］ Park D J.New Performance Function and Variable Step Size LMS Algorithm Derived by Karni and Zeng［J］.Electronics Letters，1991，27（23）：2182－2183.

［12］ 高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29（8）：1904－1907.

［13］ Douglas S C，Meng T H Y.Normalized Data Nonlinearities for LMS Adaptation［J］.IEEE Transactions on Signal Processing，1994，42（6）：1352－65.

［14］ Ramadan Z，Poularikas A.Performance Analysis of a New Variable Step－size LMS Algorithm with Error Nonlinearities［C］／／Proceedings of the Annual Southeastern Symposium on System Theory，Proceedings of the 36th Southeastern Symposium.Atlanta，2004：384－388.

Analysis of Kinds of LMS Algorithms in Application of Filtering Compensation for Magnetic Bearings

Gao Hui Xu Longxiang
Nanjing University of Aeronautics and Astronautics，Nanjing，210016

The time－variable unbalance interference signals exist synchronous with rotor rotational speed in active magnetic bearings system，which will affect the control effects of the system.To filter the unbalance signals，one kind of relatively suitable filter algorithm was proposed through analyzing some kinds of least mean square（LMS）algorithms.According to the real－time variation of the amplitudes and frequency of the interference signals in AMB system，the original LMS algorithm proposed was improved，and the filter effects on time－variable signals about the original and the improved algorithms were compared.The simulation and experimental results show that the new improved LMS algorithm has better ability of following the anticipant signals and convergence to timevariable and small amplitude signals.It can provide convenience to real－time filter compensation for the AMB system.

active magnetic bearing（AMB）；frequency mismatch；variable step－size LMS algorithm；frequency time－varying；adaptive filtering

TN911.72；TP274.2

1004—132X（2011）01—0009—06

2010—03—17

国家高技术研究发展计划（863计划）资助项目（2006AA05Z205）；江苏省自然科学基金资助项目（BK2007590）；航空科学基金资助项目（2008ZB52018）

（编辑 郭 伟）

高 辉，男，1981年生。南京航空航天大学机电学院博士研究生。主要研究方向为主动磁悬浮轴承系统不平衡振动补偿。徐龙祥，男，1959年生。南京航空航天大学机电学院教授、博士生研究生导师。