基于液压弹簧刚度的阀控非对称缸建模仿真

叶小华 岑豫皖 赵 韩 叶金杰

1.合肥工业大学，合肥，230009 2.安徽工业大学，马鞍山，243002

当xv＜0，即滑阀阀芯向右移动时，定义流进和流出非对称缸的流量比：

由式（5）和式（9）可知，阀控非对称缸的功率级滑阀的线性化流量方程在形式上是一致的，可以写为

但是在两个方向上的零位流量增益和零位流量－压力系数是不同的，所以系统在两个方向上的稳定性、响应速度和控制精度是不同的。

液压弹簧刚度是指液压缸两工作腔完全封闭时，在外负载和液压泵的作用下，因油液压缩性所形成的动态弹簧刚度［7］。现假设：① 液压缸无摩擦无泄漏；②液压缸两工作腔充满高压液压油，并完全封闭；③ 有效体积弹性模量βe为常数；④忽略黏性阻力和液动力。

如图2a所示，因活塞在移动过程中非对称缸两腔油液始终存在压力，所以可等效为如图2b所示的质量、液压弹簧系统，由虎克定律得

基于液压弹簧刚度的阀控非对称缸建模仿真

叶小华1，2岑豫皖2赵 韩1叶金杰2

1.合肥工业大学，合肥，230009 2.安徽工业大学，马鞍山，243002

针对一般方法建模时所定义的负载压力未能充分考虑非对称缸结构的不对称性和初始位置时液压弹簧刚度并非最小的问题，提出用等效承压面积加权平均的方法重新定义负载压力，推导出了滑阀线性化流量方程；利用液压弹簧刚度理论分析液压固有频率最小时非对称缸的初始位置和总容积，建立了阀控非对称缸的数学模型，提出了相应的设计准则，通过仿真和试验分析了该模型的动态特性，且与一般模型进行了比较。结果表明，该模型较一般模型更精确，更接近工程实际。

非对称缸；液压弹簧刚度；建模；仿真

0 引言

非对称缸较对称缸来说具有体积小、结构简单、承载能力大等优点，在工程中得到广泛应用。由于非对称缸结构的不对称性，给建模和控制带来了困难，其建模问题也成为近年来国内理论界关注的一个热点。然而，目前建模的主要研究重点放在负载压力和负载流量的定义上，文献［1－2］定义负载压力时没有考虑非对称缸结构的不对称性，文献［3－6］定义负载压力时虽然考虑了非对称缸结构的不对称性，但存在两方面的问题：一方面是定义的负载压力是否符合工程实际的问题；另一方面是初始位置的确定以及是否应该以此认为此时的液压固有频率最低的问题。本文用等效承压面积加权平均的方法重新定义负载压力，用液压弹簧刚度理论分析非对称液压缸的初始位置和总容积，确定非对称缸最小固有频率，以建立阀控非对称缸更为精确的数学模型。

1 阀控非对称缸的数学模型

1.1 功率级滑阀的线性化流量方程

由于非对称缸结构的不对称性，使得流进和流出缸的流量不相等，需重新建立滑阀线性化流量方程。阀控非对称缸原理图见图1。

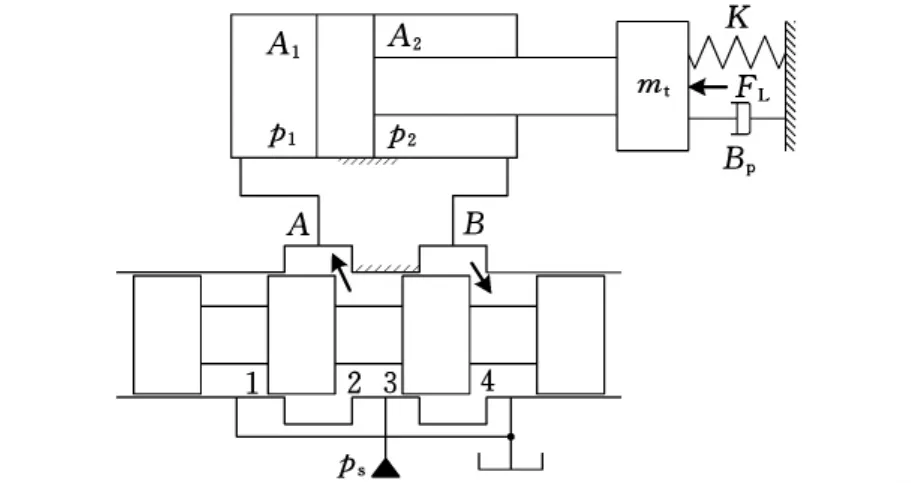
图1 阀控非对称缸原理图

当滑阀阀芯位移xv＞0，即滑阀阀芯向左移动时，定义流进和流出非对称缸的流量比：

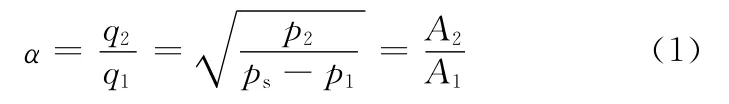
式中，α为流量比，工程上一般为0.5≤α≤1；q1为流入或流出非对称液压缸无杆腔的流量；q2为从非对称液压缸有杆腔流出或流入的流量；ps为供油压力；p1为非对称液压缸无杆腔的压力；p2为非对称液压缸有杆腔的压力；A1为非对称液压缸无杆腔的有效面积；A2为非对称液压缸有杆腔的有效面积。

式中，ε1为比例系数；Cd为各节流窗口流量系数；W 为各节流窗口的湿周；ρ为油液密度。

当xv＜0，即滑阀阀芯向右移动时，定义流进和流出非对称缸的流量比：

由式（5）和式（9）可知，阀控非对称缸的功率级滑阀的线性化流量方程在形式上是一致的，可以写为

但是在两个方向上的零位流量增益和零位流量－压力系数是不同的，所以系统在两个方向上的稳定性、响应速度和控制精度是不同的。

1.2 非对称缸的液压弹簧刚度

液压弹簧刚度是指液压缸两工作腔完全封闭时，在外负载和液压泵的作用下，因油液压缩性所形成的动态弹簧刚度［7］。现假设：① 液压缸无摩擦无泄漏；②液压缸两工作腔充满高压液压油，并完全封闭；③ 有效体积弹性模量βe为常数；④忽略黏性阻力和液动力。

如图2a所示，因活塞在移动过程中非对称缸两腔油液始终存在压力，所以可等效为如图2b所示的质量、液压弹簧系统，由虎克定律得

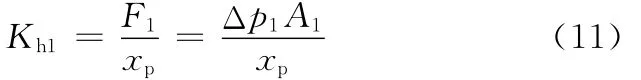
式中，Kh1为液压缸无杆腔的液压弹簧刚度；F1为液压缸无杆腔产生的液压弹簧力；Δp1为液压缸无杆腔的压力变化；xp为液压缸活塞的位移。

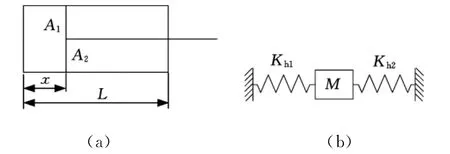
图2 液压弹簧刚度原理图

有效体积弹性模量为

式中，V1为液压缸无杆腔的容积；ΔV1为液压缸无杆腔容积的变化量。

式中，Kh2为液压缸有杆腔的液压弹簧刚度；F2为液压缸有杆腔产生的液压弹簧力；Δp2为液压缸有杆腔的压力变化；V2为液压缸有杆腔的容积。

由于活塞在移动过程中非对称缸两工作腔油液始终存在压力，所以两液压弹簧均处于压缩状态，而且是同时起作用的，所以总液压弹簧刚度可等效为液压弹簧的并联，下面来证明之。

如图2b所示，不考虑M的惯性而视其为质点，两液压弹簧在初始平衡位置时的预压缩量分别为x01和x02，再设在外力F（方向向右）作用下，质点M向右移动的位移为x，则

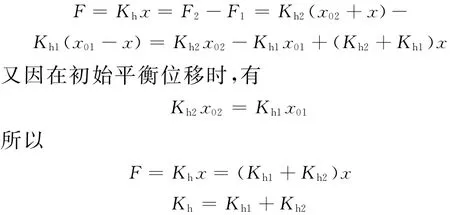
因此总液压弹簧刚度为两液压弹簧刚度Kh1和Kh2的并联，即

对阀控非对称缸系统而言，当液体压缩性影响最大，即动力元件的液压弹簧刚度最小时，其固有频率最低，阻尼比最小，这时系统的稳定性最差，所以分析时应将液压弹簧刚度最小时的活塞位置作为初始位置。

由式（15）可知，要使Kh最小，必有

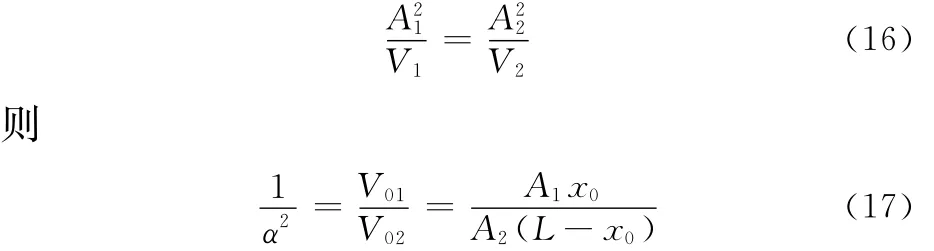
式中，V01为液压弹簧刚度最小时非对称缸无杆腔的初始容积；V02为液压弹簧刚度最小时非对称缸有杆腔的初始容积；x0为非对称缸的液压弹簧刚度最小时无杆腔侧活塞的初始位置；L为非对称缸的最大行程（图2a）。

1.3 非对称缸的流量连续性方程

定义非对称缸在无杆腔进油、有杆腔回油、活塞杆伸出时的工况为工况一，此时负载流量为

定义非对称缸在有杆腔进油、无杆腔回油、活塞杆缩回时的工况为工况二，此时也按上述方法分析可知

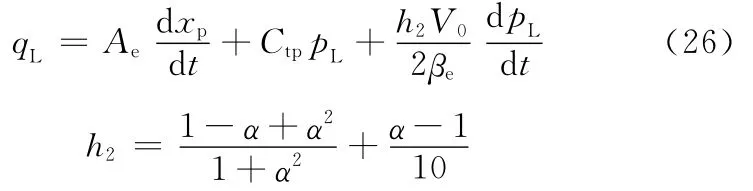
式中，h2为比例系数。

1.4 非对称缸的力平衡方程

非对称缸在工况一时，结合式（2）有

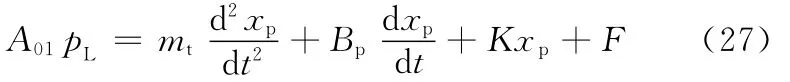
式中，mt为活塞及负载折算到活塞上的总质量；Bp为活塞及负载的黏性阻尼系数；K为负载弹簧刚度。

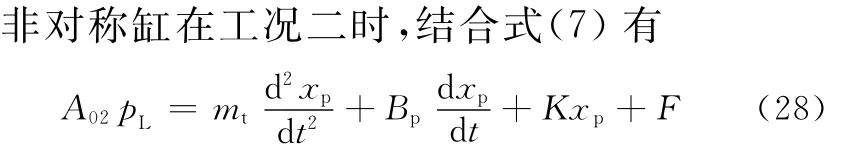
1.5 非对称缸的数学模型

在考虑负载时，以惯性负载为主，而弹性负载很小，可忽略不计，即K＝0。

首先分析非对称缸在工况一时的非对称缸数学模型。

在零初始条件下，对式（5）、式（25）和式（27）进行拉氏变换，并消去中间变量，经化简，可得非对称缸的活塞位移xp对功率级滑阀的阀芯位移xv的传递函数：

式中，ωh1为工况一时动力元件的液压固有频率；ζh1为工况一时动力元件的液压阻尼比。

下面分析非对称缸在有杆腔进油、无杆腔回油情况下活塞杆缩回时的非对称缸数学模型。

在零初始条件下，对式（9）、式（26）和式（28）进行拉氏变换，并消去中间变量，经化简，可得非对称缸的活塞位移xp对功率级滑阀的阀芯位移xv的传递函数：

综上所述，因阀控非对称缸在两个方向上的液压固有频率、液压阻尼比和零位流量增益不同，为设计和控制带来困难，所以可将式（29）和式（30）统一合并成下式：

并有针对地选取零位流量增益。为此，提出具体设计准则：在进行系统稳定性分析设计时取零位流量增益为kq10，在进行响应速度和稳态误差计算时取零位流量增益为kq20。

用本模型计算的液压固有频率比一般模型计算的液压固有频率［2-5］要小，但阻尼比一般模型稍大。

2 实例仿真与试验

在阀控非对称缸驱动的某带钢卷取对中控制（CPC）电液位置控制系统中，在设计过程中采用了本文所建立的数学模型和提出的设计准则。具体仿真参数如下：液压系统的供油压力ps＝7.0MPa，油液的有效体积弹性模量βe＝700MPa，密度ρ＝0.9×103kg／m3，活塞及负载折算到活塞上的总质量mt＝4000kg，伺服阀的固有频率ωsv＝376.92rad／s，参数ζsv＝0.44，功率级滑阀阀芯直径d0＝13mm，非对称缸活塞直径D＝80mm，杆径d＝50mm，行程L＝300mm，总泄漏系数Ctp＝5.0×10－11m3／（s·Pa），黏性阻尼系数Bp＝1.0×103N·s／m。

图3所示为不同模型的正弦响应仿真曲线与试验曲线，可以看出，本文模型的仿真曲线较一般模型［2－5］能更好地接近试验曲线。从图3中还可以看出，一般模型较实际系统超前，这与工程实际是不相符的。超前的原因是由于非对称缸处于初始位置时液压弹簧刚度并非最小，从而导致液压固有频率计算值偏大，液压阻尼比的计算值偏小，最终使模型的响应偏快。图4所示为不同模型的正弦响应误差曲线，可以看出，本模型比一般模型的误差更小。图3和图4表明，本模型的控制精度比一般模型高，这也证明了所建立的模型和提出的设计准则是正确可靠的。

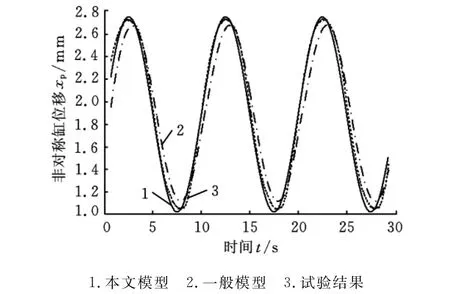
图3 不同模型的正弦响应仿真及试验曲线

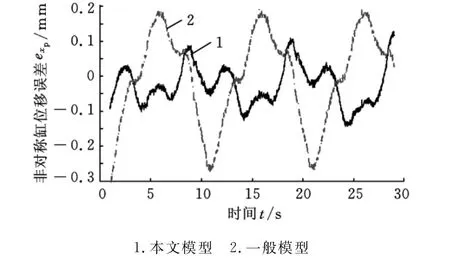
图4 不同模型的正弦响应误差曲线

图5所示是分别采用本文所建模型和一般模型的阶跃响应仿真曲线与试验阶跃响应曲线的比较，可以看出，本模型仿真曲线比一般模型更接近试验曲线，仿真曲线的超调小，在峰值时间内比一般模型振荡次数明显减少。结果表明，本文所建模型的仿真动态性能优于一般模型，且更接近工程实际。

3 结论

（1）本文提出用等效承压面积加权平均的方法定义负载压力是符合实际且有效的。

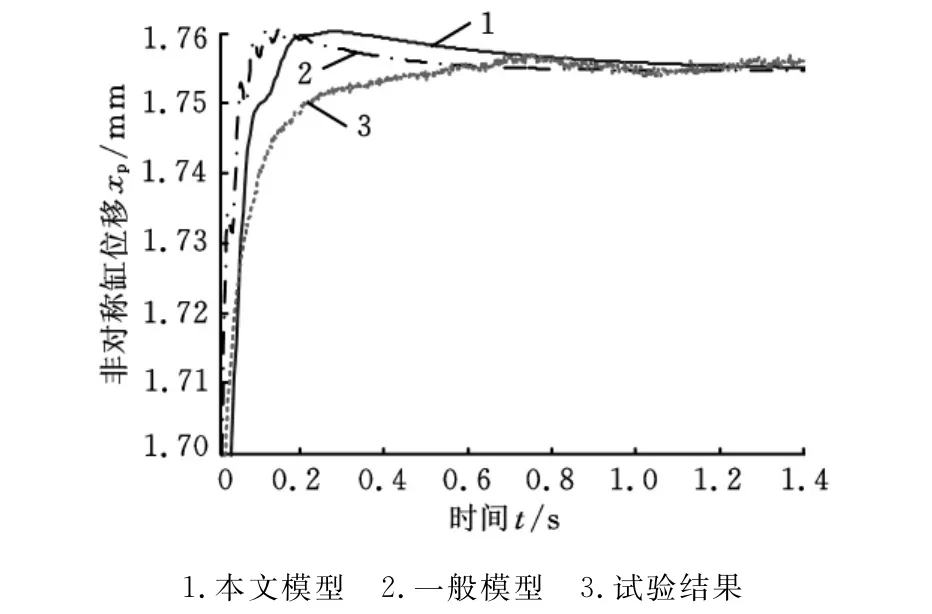
图5 不同模型的阶跃响应仿真及试验曲线

（2）利用液压弹簧刚度理论所建立的阀控非对称缸的数学模型是正确可靠的，且模型的控制精度和仿真动态性能优于一般模型，更接近工程实际。

（3）本文所提出的设计准则是正确合理的，满足工程实际的需要。

［1］ He Xuesong，Wang Xuyong，Feng Zhengjin，et al.Nonlinear Modeling of Electrohydraulic Servo Injection Molding Machine Including Asymmetric Cylinder［C］／／Proceedings of the American Control Conference.Denver，CO，United States，2003：3055－3059.

［2］ Nascutiu L.Feedback Linearization of the Doubleand Single－rod Hydraulic Servo Actuators［C］／／2006IEEE International Conference on Automation，Quality and Testing，Robotics，AQTR.Cluj－Napoca，Romania，2006：149－154.

［3］ 吴振顺.液压控制系统［M］.北京：高等教育出版社，2008.

［4］ 王传礼，丁凡，李其朋，等.对称四通阀控非对称液压缸伺服系统动态特性研究［J］.中国机械工程，2004，15（6）：470－474.

［5］ 王栋梁，李洪人，张景春.非对称阀控制非对称缸的分析研究［J］.济南大学学报（自然科学版），2003，17（2）：118－121.

［6］ 孟亚东，李长春，张金英，等.阀控非对称缸液压系统建模研究［J］.北京交通大学学报，2009，33（1）：66－70.

［7］ 王春行.液压控制系统［M］.北京：机械工业出版社，1999.1951年生。安徽工业大学校长、教授，合肥工业大学机械与汽车工程学院博士研究生导师。赵 韩，男，1957年生。合肥工业大学副校长、教授、博士研究生导师。叶金杰，男，1962年生。安徽工业大学机械工程学院高级试验师。

Modeling and Simulation of Hydraulic Spring Stiffness－based Asymmetrical Cylinder Controlled by Valve

Ye Xiaohua1，2Cen Yuwan2Zhao Han1Ye Jinjie2
1.Hefei University of Technology，Hefei，230009
2.Anhui University of Technology，Maanshan，Anhui，243002

Focusing on load pressure defined by asymmetrical struction of cylinder，which was sufficiently considered，and hydraulic spring stiffness was not minimal on the initial position in general modeling method，a method was proposed，that effective supporting area was weighted and meaned，and the load pressure was redefined，so flow equation for slide valve was of linearization.The initial position and total volume of asymmetrical cylinder were analyzed by applying the theory of hydraulic spring stiffness when its natural frequency was minimum，a mathematical model for asymmetrical cylinder was established，and relevant design rules were developed，dynamic characteristics of the model were analyzed by simulation and experiments，and compared with general model.The results show，this model is more accurate than general model，and more near to real system.

asymmetrical cylinder；hydraulic spring stiffness；modeling；simulation

TH137

1004—132X（2011）01—0023—05

2010—03—25

安徽省教育厅自然科学重点研究项目（JK2009A149）；安徽工业大学创新团队资助项目（TD200907）；安徽工业大学青年教师科研项目（QZ200815）

（编辑 郭 伟）

叶小华，男，1973年生。合肥工业大学机械与汽车工程学院博士研究生，安徽工业大学机械工程学院讲师。主要研究方向电液伺服／比例系统建模、控制和故障预报。岑豫皖，男，