基于综合智能计算的数控系统误差补偿
2011-02-01曾黄麟陈顺玲
曾黄麟 孙 勇 陈顺玲
四川理工学院 ,自贡,643000
基于综合智能计算的数控系统误差补偿
曾黄麟 孙 勇 陈顺玲
四川理工学院 ,自贡,643000
提出一种基于综合智能计算的数控系统位置控制方法,其基本思想是,在现有的数控系统内部嵌入一个神经网络的小型系统(采用插件形式嵌入),利用综合智能计算,得出系统补偿误差,实现对数控系统误差补偿的智能控制。综合智能计算通过应用粗集理论对决策表进行属性约简,利用主元分析进行数据压缩及特征提取,以降低BP网络的输入维数,缩短网络的训练时间,并利用蚁群算法对BP网络参数进行全局搜索,实现网络快速收敛到全局最优值。试验仿真表明,此方法可有效提高系统补偿精度和实时性。
BP网络;粗集理论;主元分析;蚁群算法
0 引言
数控加工误差一般来源于以下几个方面:数控机床本身零部件和结构的几何误差、数控机床由于热变形产生的误差(简称热误差)、数控机床运动机构的运动误差、数控加工时切削力变化引起的误差、数控插补算法引起的误差等。其中几何误差和热误差是数控加工时的主要误差源,由于几何误差比较稳定也比较容易测量,其补偿相对比较简单,因此热误差是精密加工中的重点。
在热误差补偿中,由于车床的加工精度是其不同构件综合作用的结果,而各构件由于结构和尺寸的差异具有不同的热容量、导热系数、热膨胀系等,且环境热源及测量机的传热边界状态难以确定,加之热变形的非线性和对温度场变化的时滞性,导致热误差的产生为一动态过程,且具有非线性的特点,因此采用如经验公式、有限元法、实验法、回归法等进行补偿,效果都不佳。利用模糊控制和神经网络结合后,可以获得较好的结果,但模型的计算量相对于其他模型要大得多[1-3]。
本文提出一种在现有的数控系统内部嵌入一个基于综合智能计算的神经网络补偿控制的小型系统,实现实时误差补偿,并针对目前采用的BP神经网络补偿方法存在的问题,应用粗集理论对温度测点进行优化,利用主元分析进行数据压缩及特征提取,降低补偿控制网络的输入维数,并利用蚁群算法对补偿控制网络参数进行全局最优化,达到对数控加工中的热误差进行实时精确误差补偿的目的。
1 热误差补偿控制系统
在通常的热误差补偿中,热误差补偿具有多因素非线性特性,利用神经网络建立热误差补偿模型,有利于车床加工的热误差补偿。一种基于综合智能计算的神经网络的数控加工热误差补偿系统如图1所示。
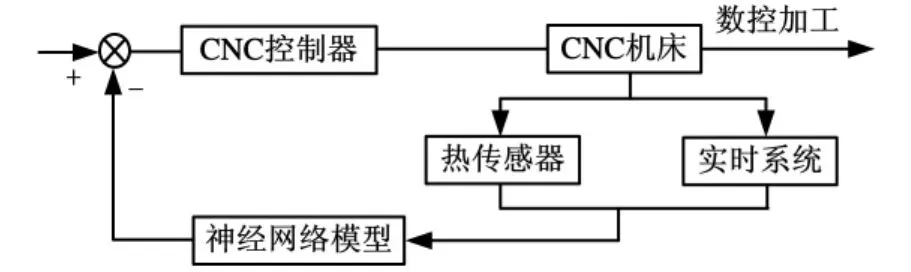
图1 基于神经网络的数控加工热误差补偿系统原理图
车床加工的热误差补偿是通过数控系统的位置控制来实现的,而热误差的产生是一动态过程,为了达到实时误差补偿的目的,我们提出在现有的数控系统内部嵌入一个神经网络补偿控制的小型系统,嵌入的地点是位置/速度控制单元。数控系统的位置实时控制系统如图2所示。
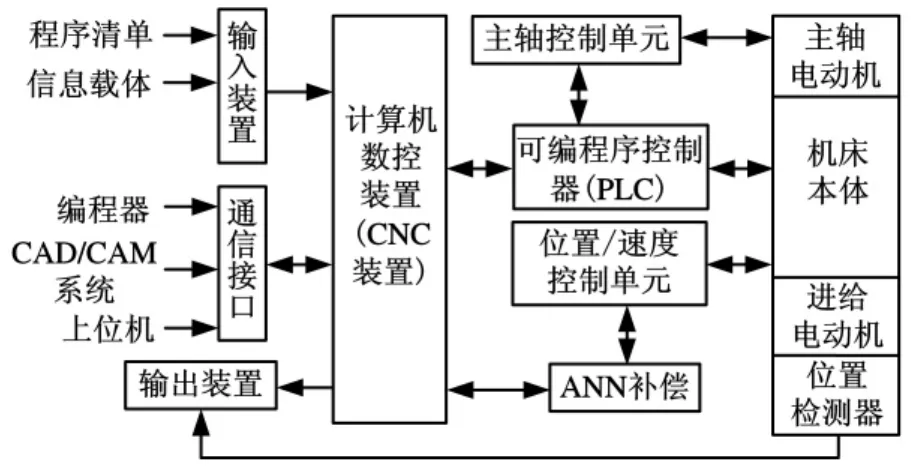
图2 数控系统的位置实时控制系统
在零件加工过程中,数控系统的位置实时控制系统每次调用插补程序,都能计算出本次插补周期内各坐标轴的位置增量,据此求得各坐标轴相应的位置,并与采样所获得的实际位置(反馈值)进行比较,从而获得位置跟踪误差。机床系统中嵌入一个基于综合智能计算的神经网络数控加工热误差补偿系统,就能在每个采样周期内实时预测出由于温度、几何误差等因素的影响而产生的位置误差,从而完成数控加工热误差的实时精确补偿。
2 基于综合智能计算的神经网络控制系统的实现
2.1 基于粗集理论的机床热补偿误差的温度测点优化
在热误差补偿中,温度测点的选择从几个到几百个不等。温度测点过多会使布置测点的工作量加大,存在实时性差、补偿系统复杂等缺点;温度测点布置得太密会使相邻测点的输出信号有较大的相关性,影响计算精度。为了从众多的温度测点中选出适当数目的测点,就需要对机床热补偿误差的温度测点进行优化。
一个机床热误差补偿系统定义为一个二元有序偶(U,R),其中U是有限个数控机床加工对象组成的论域,R是一组用以描述数控机床加工对象的温度影响属性,表现了论域U上的一组二元关系(对完备信息系统而言,它通常是一组等价关系)。对任意的r∈R,其论域U中的每一个对象赋唯一属性值。如果一个机床热误差补偿系统中的属性集R被分为热误差影响的条件属性集C和热误差影响的结果属性集D,则可以构造一个机床热误差补偿系统决策表。
根据粗集理论[4-6],现定义一个机床热误差补偿系统中热误差影响的条件属性集C和热误差影响的结果属性集D之间的关系依赖性k,若k=1表明该机床热误差补偿系统是协调的,若kR-r=1,则表明去除热误差影响条件属性r(r∈C)后该机床热误差补偿系统仍是协调的。再定义一个机床热误差补偿系统中热误差影响的条件属性集C和热误差影响的结果属性集D的等价关系之间的一致性QC,若QC=1,则表明该机床热误差补偿系统中条件属性集C和结果属性集D的等价关系是一致的,若QC-r=1,则表明去除热误差影响条件属性r(r∈C)后,该机床热误差补偿系统中条件属性集C和结果属性集D的等价关系仍是一致的。
利用粗集理论方法,可以对机床热误差补偿系统的误差影响的条件属性简化,进行温度测点优化,其步骤如下:①对机床热误差补偿系统数据进行预处理,构成一个决策表;②判定机床热误差补偿系统数据表是否协调;③根据上文所定义的一致性QC的特性,进行机床热误差补偿系统中条件属性的简化,最后求出简化的核,从而得到机床热误差补偿系统的温度测点优化结果。
本文针对一台HMC800A机床进行试验,该型号机床的主要热误差源为左右电机座温度、左右轴承座温度、左右光栅温度、环境温度、工作台温度等7个特征参数,利用粗集理论方法,分析各变量与热误差之间的相关性,最终选择出左电机座温度、右轴承座温度、右光栅温度和工作台温度4个重要特征参数,从而降低了系统输入变量的维数以及网络结构的复杂性,去掉了冗余信息,使网络的训练集合简化,缩短了网络的训练时间,提高了网络的实时性。
2.2 基于主元分析方法进行数据压缩及特征提取
主元分析[7]是将研究对象的多个相关变量转化为少数几个不相关变量的一种多元统计方法。主元分析的目的是基于Karhunen-Loeve分解,通过一个特殊的向量矩阵,将数据从原来的高维空间映射到一个低维向量空间,降维后保存了数据的主要信息,从而使数据更易于处理。
通过粗集理论方法对机床热误差补偿的温度测点进行优化后,利用主元分析进一步进行数据压缩及特征提取,这样既实现了对工业噪声的过滤,又进一步降低了数据空间的维数。本文利用主元分析对输入系统的上述4个温度输入单元进行特征提取,得到降维后不相关的3个有用温度输入变量,进一步减少了系统输入维数,从而提高了系统的实时性。
2.3 补偿控制神经网络模型的建立
数控机床的误差是一种动态数据,随材料、机床、加工时间的不同而变化,因此应该把这些影响因素由实时在线系统综合反馈到误差补偿神经网络中,这就需要提出一种动态反馈神经网络的概念[8-9]。
动态反馈神经网络要把影响数控加工热误差的补偿数据实时在线地反馈到网络的输入端,这样使得网络的输入数据始终保持较高的精确度,由于动态递归网络容易实现且具有良好的预测能力,因此在反馈网络中加入延时单元,以前面多个时刻的值去预测下一个时刻的值。一种动态反馈神经网络结构如图3所示。
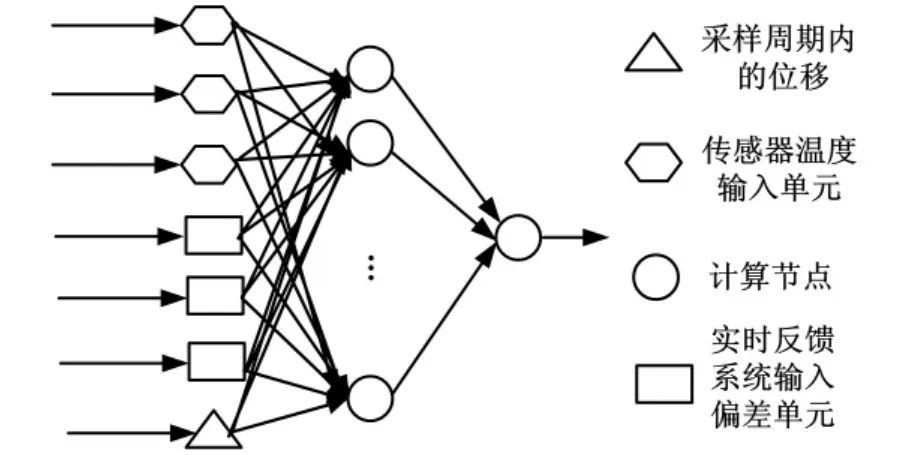
图3 一种动态反馈神经网络结构
2.4 基于蚁群算法对BP网络参数的优化训练
BP算法在神经网络参数学习中局部性能好,但易陷入局部极小值,而蚁群算法拥有良好的全局性能。根据这一特点,首先利用蚁群算法[10-11]对神经网络参数进行全局搜索训练,然后再利用BP算法对参数进行局部学习,设计出一种自适应蚁群算法,在一定程度上解决了传统蚁群算法收敛速度和拓宽搜索空间之间的矛盾。
自适应蚁群算法的基本思想是:假定网络有m个待优化参数,包括权值和阈值。首先,对这些参数进行排序,记为p1,p2,…,pm,对于其中任一参数pi(i=1,2,…,m),将其设为N 个随机非零值(在其取值区间内划分为N-1个小区间),形成集合Ipi。然后定义蚂蚁的数目S,这些蚂蚁从蚁巢出发寻找食物。每只蚂蚁从第1个集合出发,根据集合中元素的信息素状态,随机地从每个集合Ipi中选择一个元素。当蚂蚁选择完所有元素后,就到了食物源,再按原路返回蚁巢,同时调节集合中所选元素的信息素。将这一过程反复进行,当全部蚂蚁收敛到同一路径时,就找到了网络参数的最优解。
自适应蚁群算法训练神经网络的主要步骤如下[10-11]:
(1)初始条件:令集合Ipi中第i个元素的在迭代次数t=0时的信息素为τj(0),蚂蚁的数目为S,所有蚂蚁置于蚁巢,设置最大迭代次数为tmax。
(2)启动所有蚂蚁,每只蚂蚁从集合Ipi开始,按照下述路径选择规则依次在每个集合中选择一个元素,直到蚁群全部到达食物源。路径选择规则为,对于集合Ipi,任意一只蚂蚁a(a=1,2,…,S),根据下式计算的概率随机地选择其第j个元素:
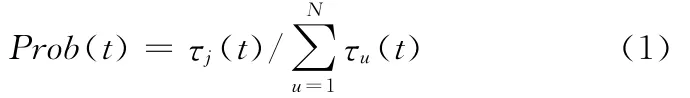
(3)当所有蚂蚁在每个集合中都选择了一个元素后,用各蚂蚁所选权值作神经网络参数计算训练样本产生的输出误差,记录当前所选参数中的最优解。设该过程经历的时间为t个时间单位(即用迭代次数表示时间单位),对所有集合Ipi中各元素的信息素按下式调整:
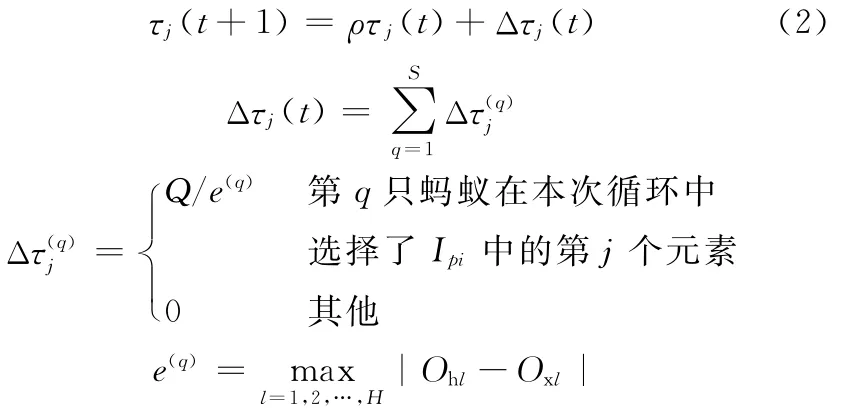
由此可见,误差越小,信息素增加越多。
(4)重复步骤(2)、步骤(3),直到所有蚂蚁全部收敛到一条路径或达到最大迭代次数,输出最优解组合,权值寻优结束。
(5)将算法最优解赋予三层前向神经网络,再用BP算法进一步训练网络,直到获得满意精度。
(6)输出结果,算法退出。
3 实验仿真
训练数据采用某机床厂提供的572组热误差数据作为样本,把所测的不同位置的温度作为条件属性 C,C = {T1,T2,T3,T4,T5,T6,T7,T8},所测的定位误差位移作为结果属性D,D={Y0,Y1,Y2,Y3,Y4,Y5.Y6,Y7,Y8,Y9,Y10},从 而 建立了一个机床热误差补偿系统。
基于蚁群算法对BP网络参数进行优化训练,误差收敛与训练循环次数的关系如图4所示。可以看出,单纯的BP算法训练3000多次并没有完全收敛,当总体均方误差值达到0.1时基本陷入局部极小,以后效果不明显,但是采用优化后的BP网络初始误差已经比较精确,细调后效果明显优于前者。
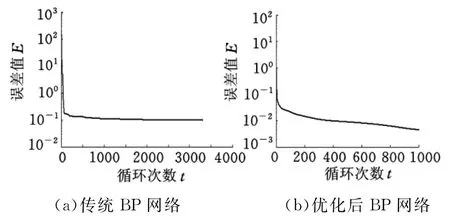
图4 网络优化训练误差收敛曲线
基于本文方法,采用基于综合智能计算的数控系统误差补偿结果如图5所示。可以看出,测试572点,其中随机抽检的数据中的110个点补偿后的误差值均不超过6μm,57个点补偿后残余误差值超过6μm,有90%以上的数据是符合精度要求的,大大提高了机床加工精度。
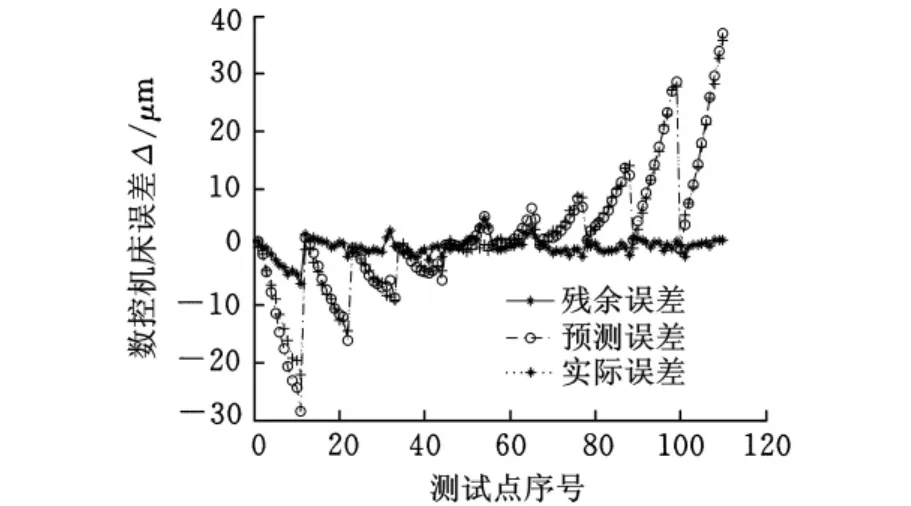
图5 基于综合智能计算的数控系统误差补偿结果
4 结束语
本文提出利用综合智能计算,建立数控机床系统热误差补偿模型,实现对数控系统的实时误差补偿智能控制。综合智能计算应用粗集理论和主元分析的方法对BP网络输入数据进行约简和压缩,显著缩短了BP网络的训练时间,提高了网络的实时性。本文采用自适应蚁群算法对网络参数进行优化,进一步提高了网络的预测逼近能力。将粗集理论、主元分析和自适应蚁群算法应用到BP网络中进行数控系统热误差补偿模型的建模是一种很好的尝试,它不仅提高了预测精度,而且也提高了系统控制的实时性。
[1] Zeng Huanglin,Sun Yong,Zhang Haiyan.Thermal Error Compensation on Machine Tools Using Rough Set Artificial Neural Networks[C]//Proceeding of WRI World Congress on Computer Science an Information Engineering.Los Angeles,USA,2009:51-55.
[2] 孙勇,曾黄麟.一种新的数控机床热误差实时补偿方法[J].机械设计及制造,2010(1):244-246.
[3] 张海燕,曾黄麟,唐建芳.基于粗集方法的机床热补偿误差的温度测点优化[J].机床与液压,2010,38(1):39-41.
[4] 曾黄麟.智能计算[M].重庆:重庆大学出版社,2006.
[5] Zeng Huanglin,Zeng Xiaohui.Studies on Consistence of the Knowledge Simplification of an Uncertain System[C]//Proceeding of 8th International Conference on Cognitive Informatics.HongKong,2009:162-166.
[6] Zeng Huanglin,Zeng Xiaohui.Reasoning Decision Rules of an Uncertain System[C]//The Fourth International Conference on Rough Sets and Knowledge Technology,Proceeding of RSKT 2009.Berlin:Springer-Verlay,2009:634-642.
[7] 胡慧,张彪.粗糙集和主元分析在基于神经网络的模拟电路故障诊断中的应用[J].自动化与仪器仪表,2009(3):35-37
[8] 贾志新,张宏斌,郗安民.基于径向基函数神经网络的电火花线切割机床可靠性数据模拟生成[J].机械工程学报,2010,46(2):145-149.
[9] 李巍华,张盛刚.基于改进证据理论及多神经网络融合的故障分类[J].机械工程学报,2010,46(9):93-99.
[10] Duan H B,Wang D B,Yu X F.Reasearch on the Optimum Configuration Strategy for the Adjustable Parameters in Ant Colony Algorithm[J].Journal of Communication and Computer,2005,2(9):32-35.
[11] Zeng Huanglin,Huang Yan,Zeng Xiaohui.A New Approach of Attribute Reduction Based on Ant Colony Optimization[C]//Proceeding of Fifth International Conference on Natural Computation.Tianjin,2009:3-7.
Error Compensation for Machine Tools Based on Integrated Intelligent Computation
Zeng Huanglin Sun Yong Chen Shunling
Sichuan University of Science and Engineering,Zigong,Sichuan,643000
This paper is a study of error compensation for machine tools based on integrated intelligent computation.The primary focus was on integrated intelligent computation approach to develop a BP neural network embed in a digital control system of a machine tool.Data compression and feature extraction was realized by way of application of RST and principal component analysis,which reduced BP network input dimension and reduced network training time.Taking advantages of ant colony algorithm,aglobal optimum of error compensation for machine tools was obtained by a BP network convergence.Positioning error compensation capabilities were tested using industrial standard equipment and procedures.The results obtained show that this approach can improve compensation precision and real time of error compensation for machine tools effectively.
BP network;rough set theory(RST);principal component analysis;ant colony algorithm
TG502.15
1004—132X(2011)01—0001—04
2010—03—15
国家科技重大专项(2009ZX04002-013);四川省教育厅基础应用研究课题(2008RZ003)
(编辑 郭 伟)
曾黄麟,男,1955年生。四川理工学院院长、教授,电子科技大学博士研究生导师。主要研究方向为人工神经网络、粗集理论、模糊逻辑、智能信息处理、模式识别等。获省部级科技进步二等奖1项、三等奖2项,市级科技进步一等奖3项、二等奖3项。出版专著8部,发表论文180余篇。孙 勇,男,1986年生。四川理工学院自动化与电子信息学院讲师、硕士。陈顺玲,女,1986年生。四川理工学院自动化与电子信息学院讲师、硕士。
