L2基的组态空间中修正Pöschl-Teller势的精确解

陈发堂， 张民仓

(1.上海电力学院数学物理系，上海200090;2.陕西师范大学物理学与信息技术学院，西安710062)

在量子力学中，寻求给定势场波动方程的精确解析解始终是人们感兴趣的问题.首先，详尽地分析这些解析解能够加深对相关物理问题的理解，进而能够为修正和完善原有的物理学理论提供有力的支撑［1-2］;其次，为了研究更为复杂的物理学系统，需要建立新的模型并引入新的计算方法，而这些解析解对于检验所建模型是否正确及进一步完善新的计算方法具有重要的意义.一般来说，获得精确解析解的方法是把给定势场的波动方程转化为确定的广义超几何方程，而方程的解能够由各类相应的正交多项式表示.量子力学中的可解势问题可分为三类，即精确可解势问题、有条件的精确可解势问题和准精确可解势问题.精确可解势问题是指当势函数参数在其定义域内连续变化时，波动方程存在解析解，并能够得到全部的能量谱;有条件的精确可解势问题则是指当势函数参数取特定值时，波动方程才存在解析解及相应的能量谱;而准精确可解势问题则是指那些只有部分能量谱可以确定的势场［3-4］.为了方便地研究量子力学中的可解势问题，已经提出和发展了许多新的理论和方法，其中包括目前广泛应用的因子分解方法［5］、群理论方法［6-7］、超对称量子力学和形不变势方法［8-9］等.

1 三对角化矩阵方案

由方程(1)容易得到，波函数展开系数满足的三项递推关系式如下：

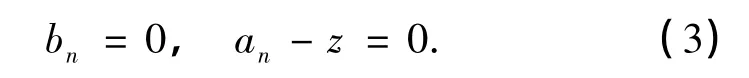
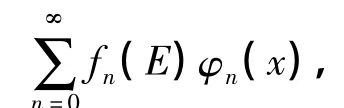
式中，An为归一化常数，Pn(x)为空间坐标x的n阶多项式，wn为满足条件wn(x±)=0的权函数，其中x-(x+)分别为空间的左(右)边界.在求解一维势场的波动方程时，有两类空间是经常用到的，其中第一类空间的x±是有限的，并且

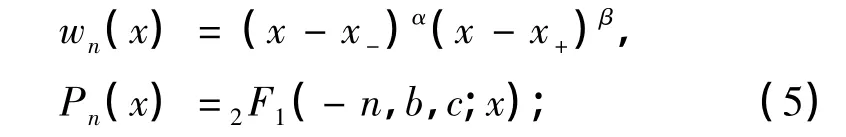
而另一类空间是半边有限的，即x-是有限的，而x+是无限的，并且

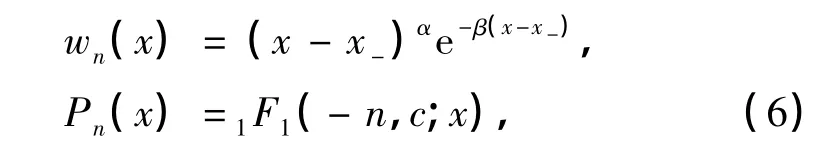
式中，2F1(-n，b，c;x)为超几何函数，1F1(-n，c;x)为合流超几何函数.参数α，β，b和c均为实数，并且α和β为正数.这些参数一般都与所研究的问题相关，而对于束缚态，这些参数也与指标n相关.

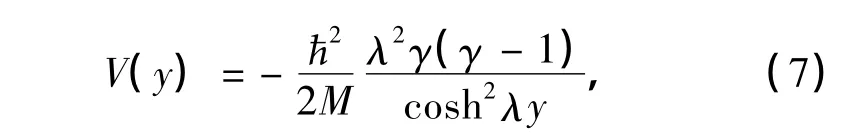
式中，参数γ取整数时，平面波经此势不发生反射，因而，修正Pöschl-Teller势也称为无反射势.由于无反射势在KDV孤子理论等问题的研究中也有重要作用，因而，近年来一直受到人们的重视［15］.

2 修正Pöschl-Teller势的精确解

质量为M的粒子在一维势场V(y)中运动时满足的与时间无关(ħ=M=1)的Schrödinger方程为

作变量替换x=tanh λy，则对应于y∈［-∞，∞］，x∈［-1，+1］，因而，一维修正Pöschl-Teller势满足的Schrödinger方程符合式(5)给出的具有边界x= ±1的情况.由于超几何函数2F1(-n，b，c;x)可以由Jacobi多项式(x)表示，于是在L2空间中满足边界条件的基函数可以选为

式中，α，β＞0，μ，ν＞-1，并且归一化常数为

利用下面所给的Jacobi多项式满足的微分方程和微分公式［10］：

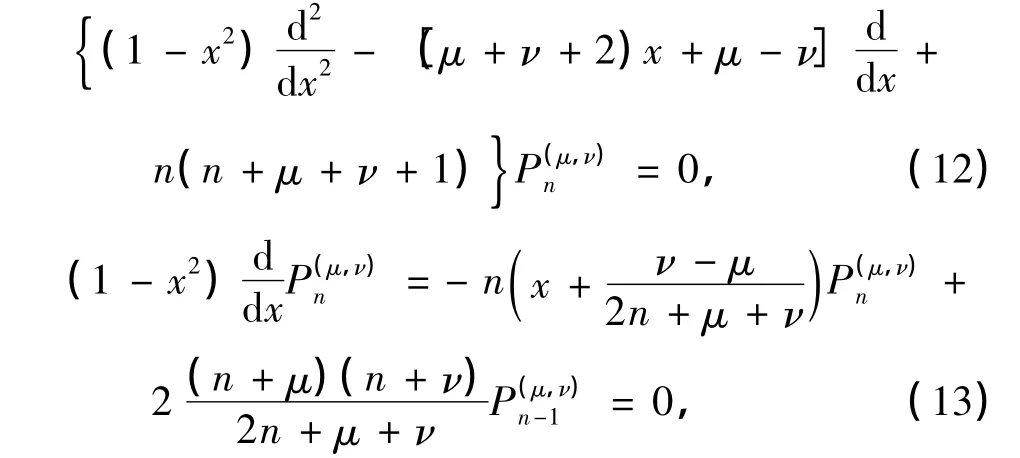
可以得到

在式(14)的推导中利用了如下关系式：

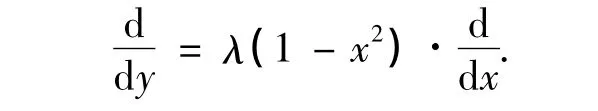
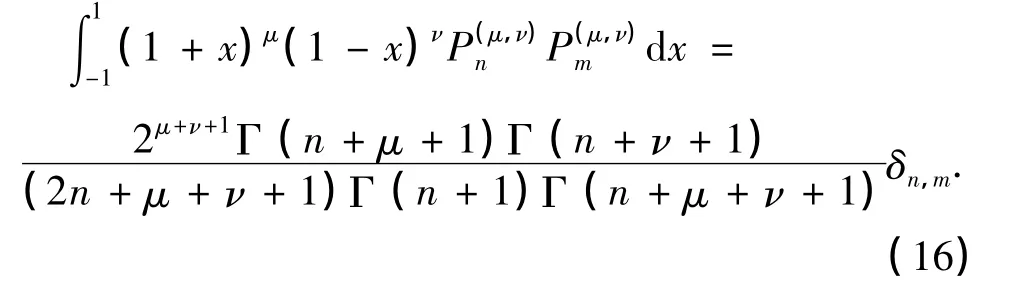
最后，可以得到

式中，参数ν和μ必须满足关系ν=μ，并且

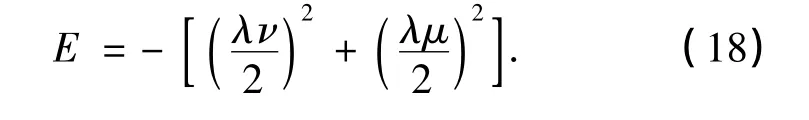
由式(18)可以看出，参数ν和μ与能量相关.由于能量是负的，因而一维修正Pöschl-Teller势满足的与时间无关的Schrödinger方程必存在E＜0的束缚态解.另外，波函数系数的展开式(17)中并没有出现式(2)中的bnδn，m-1和bn-1δn，m+1项，这是因为，对参数α和β的合适选取能够实现三对角化矩阵的对角化.由式(3)和(18)，容易求出与束缚态相对应的分立能谱为

这一结论与其他方法得到的结果相一致［2］.由于n= 0，1，…，因而从方程(19)可以看出，当参数γ=n+ 1，即γ取整数时，一维修正Pöschl-Teller势无束缚态存在.最后，得到的束缚态波函数为

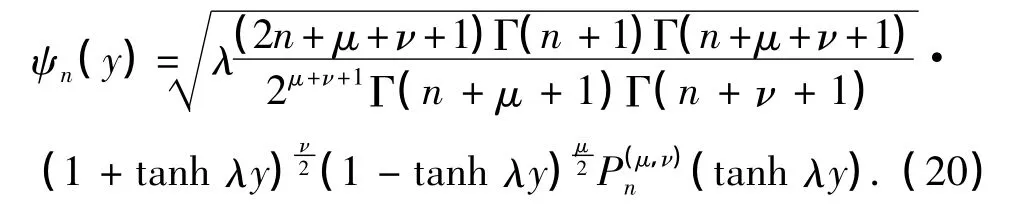
3 结束语

本工作是在L2基的组态空间中求解了一维修正Pöschl-Teller势满足的Schrödinger方程，由于L2函数空间能够负载波算子的三对角化矩阵表示，因而求解Schrödinger方程转化成为寻求波函数展开系数满足的三项递推关系式.在大多数情况下，这个递推关系式容易由熟知的正交多项式的相关性质得到，而束缚态的能谱方程可以由这个递推关系式的对角化条件得到.以上的研究过程表明，合适地选择势场相关参数，能够容易实现波函数展开系数递推关系式的对角化.另外一维修正Pöschl-Teller势的Schrödinger方程具有E＜0的束缚态解，相应的束缚态波函数可以由Jacobi多项式表示;当势场参数γ取整数时，一维修正Pöschl-Teller势无束缚态存在.

［1］ SCHIFFL I.Quantum mechanics［M］.3rd ed.New York：McGraw-Hill，1955.

［2］ FLÜGGES.Practical quantum mechanics［M］.Berlin：Springer，1974.

［3］ DESOUZA-DUTRA A.Conditionally exactly solvable class of quantum potentials［J］.Physical Review：A，1993，47：R2435.

［4］ NAG N， ROYCHOUDHURY R， VARSHNIY P.Conditionally exactly solvable potentials and supersymmetry［J］.Physical Review：A，1994，49：5098-5099.

［5］ DONGS H.Factorization method in quantum mechnics［M］.Netherlands：Springer，2007.

［6］ BANDERM，ITZYKSONC.Grouptheoryandthe hydrogen atom(Ⅰ)［J］.Reviews of Modern Physics，1968，38：330-345.

［7］ ALHASSIDY，GURSEYF，IACHELLOF.Potential scattering，transfer matrix，and group theory［J］.Physical Review Letters，1983，50：873-876.

［8］ COOPERF，KHAREA，SUKHATMEU.Supersymmetry and quantum mechanics［J］.Physics Reports，1995，251：267-385.

［9］ 黄博文，王德云.含有非谐振势系统能谱的研究［J］.物理学报，2002，51：1163-1166.

［10］ ALHAIDARIA D.AnextendedclassofL2-series solutions of the wave equation［J］.Annals of Physics，2005，317：152-174.

［11］ ALHAIDARIA D，BAHLOULIH.Electron in the field of a molecule with an electric dipole moment［J］.Physical Review Letters，2008，100：110401.

［12］ BAHLOULIH，ABDELMONEM，M S，NASSERI M.Analytical treatment of the Yukawa potential［J］.Physica Scripta，2010，82：065005.

［13］ ELAAOUDE，BAHLOULIH，ALHAIDARIA D.Onedimensional solvable potentials in a tridiagonal representation space［J］.InternationalReview of Physics，2008，2：5.

［14］ 陈刚，楼智美.无反射势阱中相对论粒子的束缚态［J］.物理学报，2003，52：1071-1074.

［15］ NOGAMIY，TOYAMAF M.Transparent potential for the one-dimensional Dirac equation［J］.Physical Review：A，1992，45：5258-5261.

［16］ 刘式适，刘式达.特殊函数［M］.2版.北京：气象出版社，2002.