一类拟线性抛物型方程的非局部边值问题

周长亮， 王远弟

(上海大学理学院，上海200444)

本工作研究如下具有非局部边界条件的拟线性偏微分方程问题：

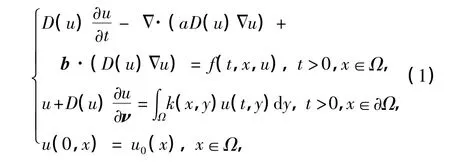
式中，Ω为 Rn中有界的区域，具有边界∂Ω∈C2+α(0＜α＜1)表示∂Ω的外法方向向量，其中函数k(x，y)，D(u)满足k(x，y)∈C1+α()×C()且k(x，y)≥0，D(u)在R上二阶连续可导且D(u)= D(-u)，D(u)＞γ＞0.系数a=a(t，x)，b(t，x)= (b1(t，x)，b2(t，x)，…，bn(t，x))，f(t，x，u)是给定的满足本文第1节中条件(H1)的函数.

拟线性抛物型偏微分方程问题起源于具有内部热源的热传导等研究，其中温度u(t，x)满足如下方程：

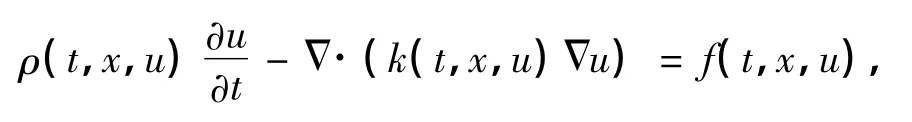
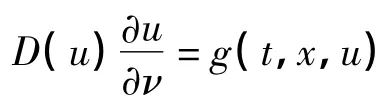
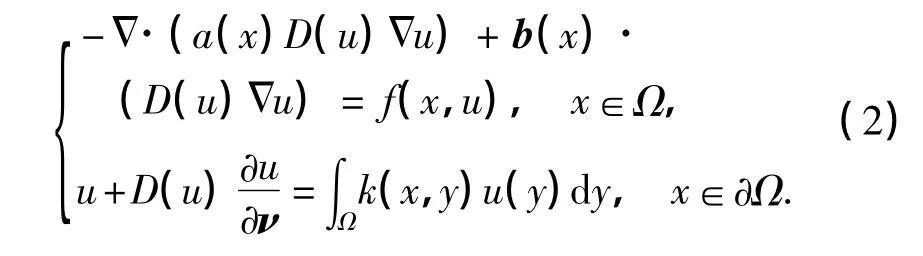
本工作主要运用上、下解和相应的单调迭代方法研究问题(1)解的存在唯一性和问题(2)最大、最小解的存在性，以及发展方程解收敛到平衡问题最大、最小解的渐近行为，并将文献［1］等的结果推广到拟线性抛物型方程的非局部边值问题.最后，考察了发展方程解收敛到平衡问题最大、最小解的渐近性态.

1 抛物型方程解的存在性和唯一性

任意给定正实数T，记DT=Ω×(0，T］，ST=∂Ω×［0，T］.Cα(Q)为Q中指数为 α∈(0，1)的Hölder连续函数空间(Q为Rn或Rn+1中任意的区域).Cm(Ω)为Ω内m阶连续可导函数的集合，C1，2(DT)为(t，x)∈DT内关于t一阶连续可微和关于x二阶连续可微函数的集合.

本节中假设条件(H1)成立.为了有效地研究问题(1)，引入变换

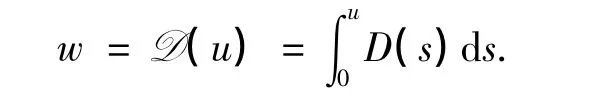
由于D'(u)=D(u)＞0，故存在反函数u= q(w)，因此，在该变换下，问题(1)转化为

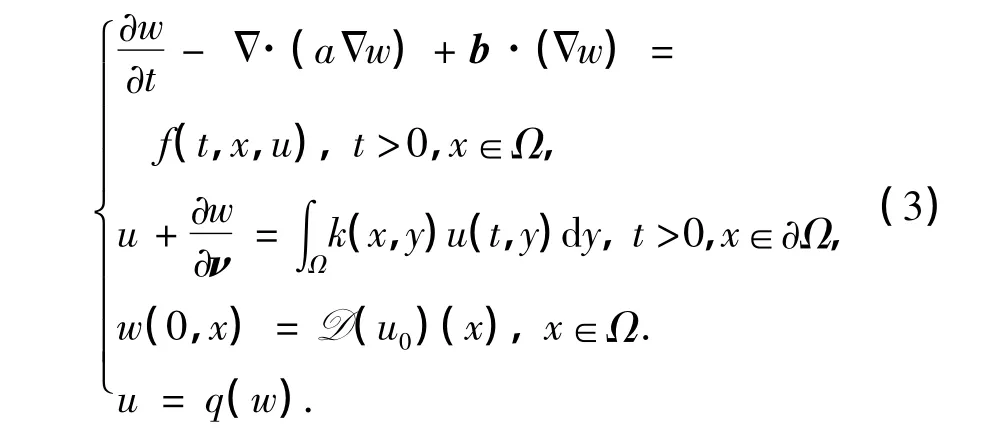
接下来，给出问题(1)和(3)的上、下解的定义.

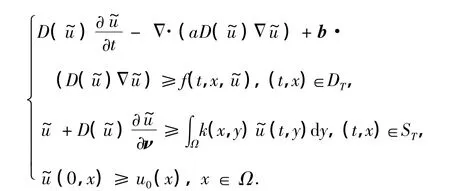
出于研究问题(1)上、下解的有序性及解的存在唯一性的需要，首先研究如下线性不等式问题：

证明 当k(x，y)不恒等于0时(k(x，y)=0为平凡的)，令

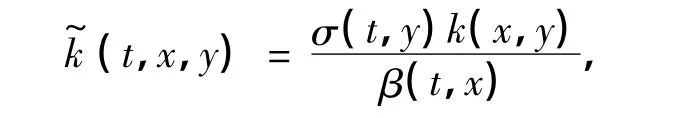
由文献［7］可知，能够找到正函数φ(x)∈C2()，使得φ(x)满足

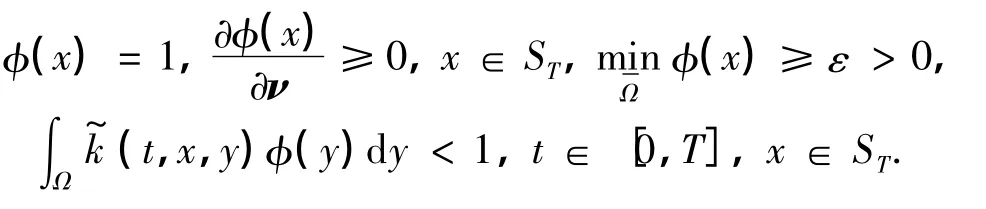
引入变换z=eλt，式(4)可以转化为

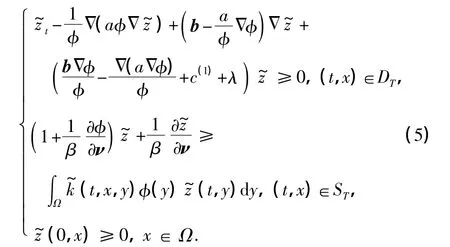
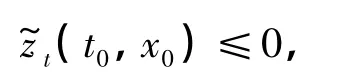
当(t0，x0)∈ST时，可以得到，代入式(5)，得矛盾.

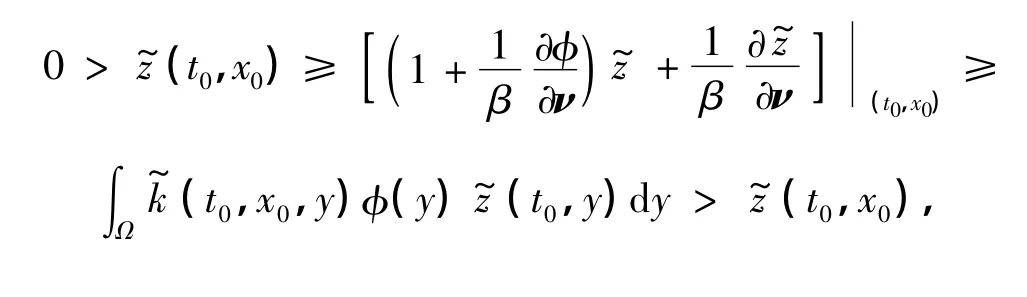
其中

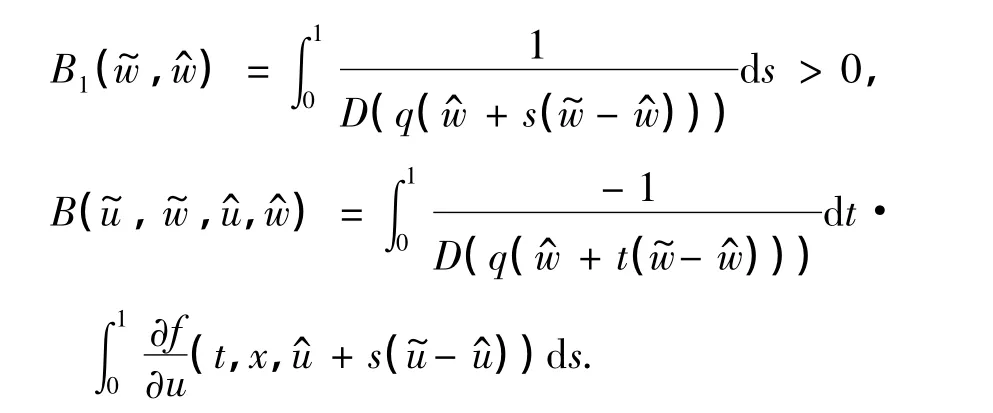
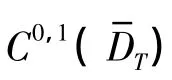
证明 u(t，x)可以看作初值条件为v(0，x)的问题(1)的上解，依据引理2可得u(t，x)≥v(t，x).得证.

引理2说明问题(1)的上、下解是有序的.现以上、下解为初始值构造迭代序列来讨论解的存在性.由于D'(u)=D(u)＞γ＞0，则存在常数γ(1)＞0，使得γ(1)D'(u)-1≥0.

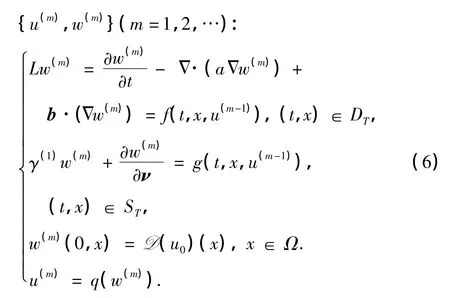
把u(m-1)看成是已知的情况下，式(6)是关于w(m)的方程，由文献［8］中的定理5.3可以得到在DT上方程解w(m)的存在性.

当初始迭代u(0)=时，用序列表示迭代序列{u(m)，w(m)}，其中当初始迭代时，用序列表示迭代序列{u(m)，w(m)}，其中

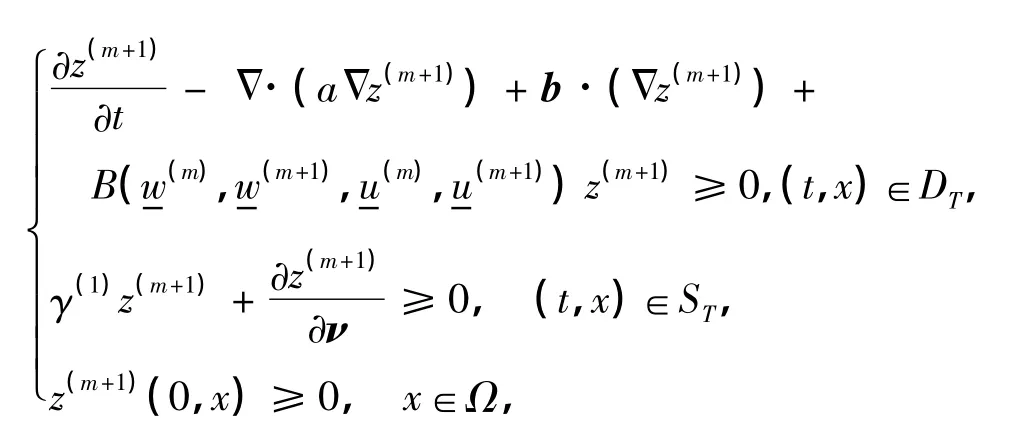
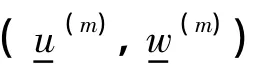
设微分算子L的基本解为Γ(t，x;ζ，ϵ)，由文献［9］可知，问题(6)中的w(m+1)可以表示为

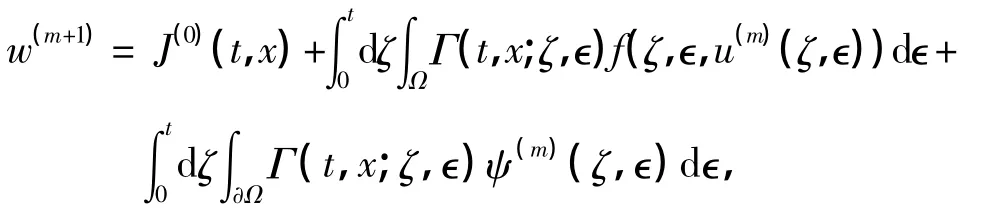
式中，

近日，Nutrien公布了2018年第三季度财务报告。“第三季度，Nutrien取得了稳定的经营业绩，零售利润同比增长10%。而营养品生产业务报告了更高的产量、利润率和显著降低的成本。我们还在战略重点上取得了重大进展，包括提高股息和协同目标、完成股票回购计划以及完成出售阿拉伯钾肥公司(APC)股份。我们仍将继续从出售的股权投资中获得50亿美元的净收入。由于市场基本面强劲，合并协同效应加速，Nutrien也提高了年度指引。我们将继续保持良好的定位，以提供强劲的长期股东回报。”Nutrien总裁ChuckMagro说道。

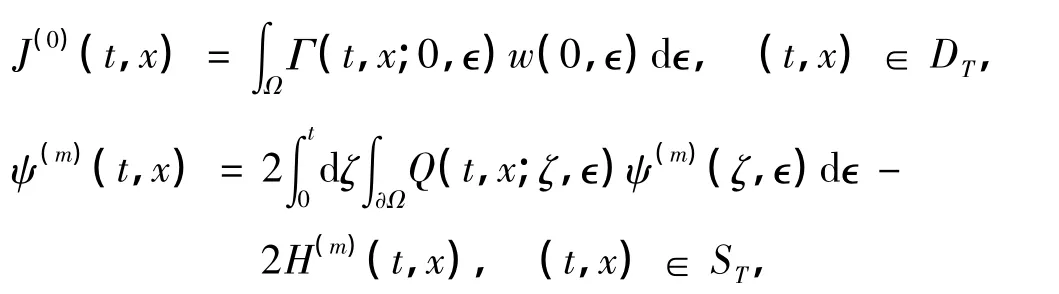
其中

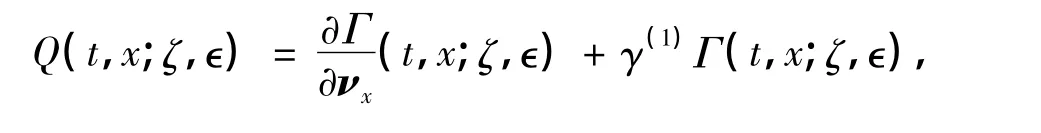
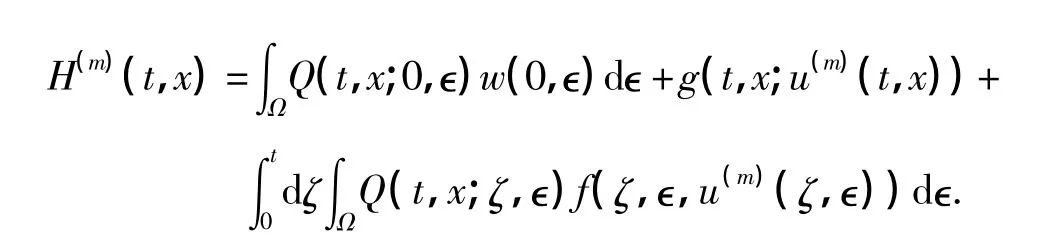
对任意的(t，x)∈ST，k(x，y)u(m)(t，y)是有界的，因此，由控制收敛定理，可得

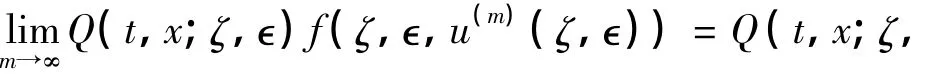
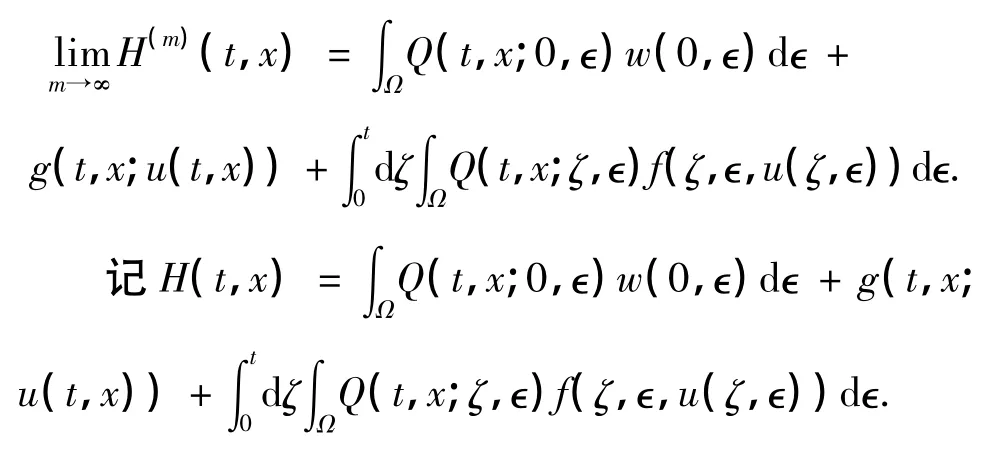
由文献［9］中ψ(t，x)的表达式可知，ψ(t，x)在ST上有界，因此，可得{ψ(m)(t，x)}在 ST上一致有界.

由于

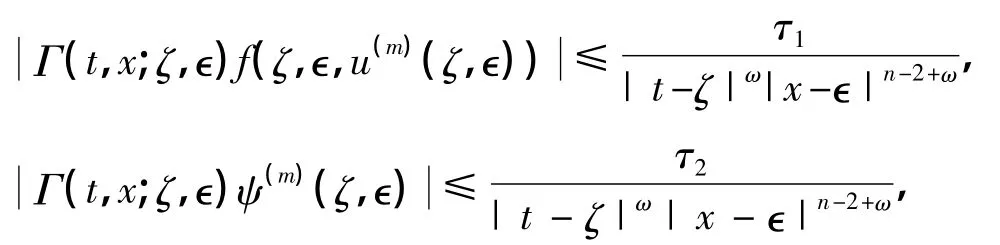
式中，0＜ω＜1，τ1，τ2均为正常数，因此，由控制收敛定理可知，w(t，x)满足

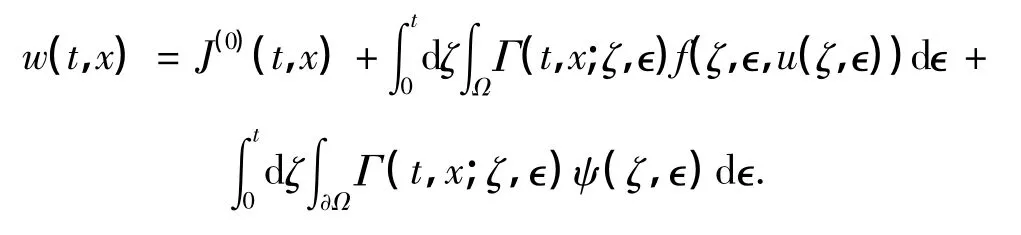
由文献［9］中的引理2.2可知，ψ(t，x)在ST上也是连续的.又由文献［9］中的引理1.2可得，w(t，x)在上Hölder连续，因u=q(w)二阶连续可导，可得u(t，x)在上Hölder连续，即

若u1，u2是问题(1)的解，由推论1可得，u1≤u2，u1≥u2，故u1=u2.得证.

2 椭圆方程问题

平衡问题(2)在变换u=q(w)下可以转化为如下问题：

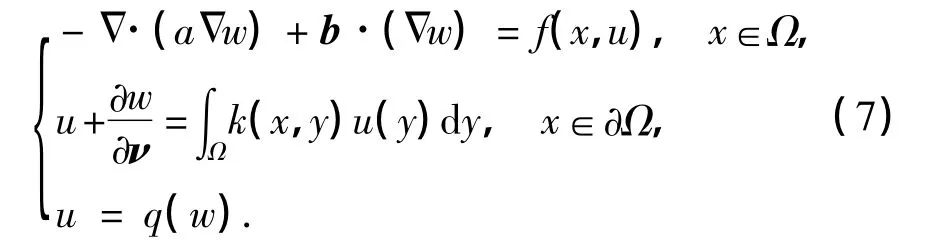
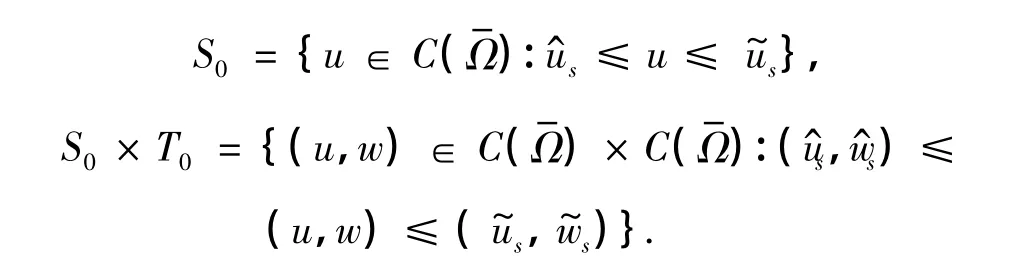
由于D'(u)=D(u)＞γ＞0，则存在常数γ(2)＞0，γ(3)＞0，使得

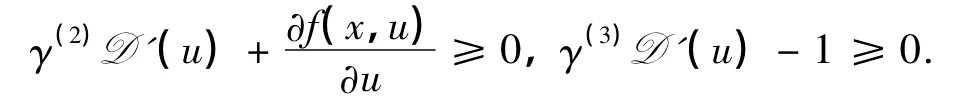
记

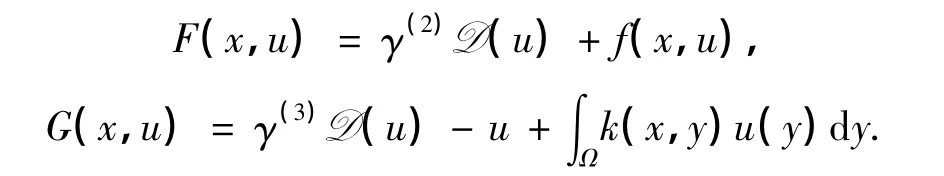
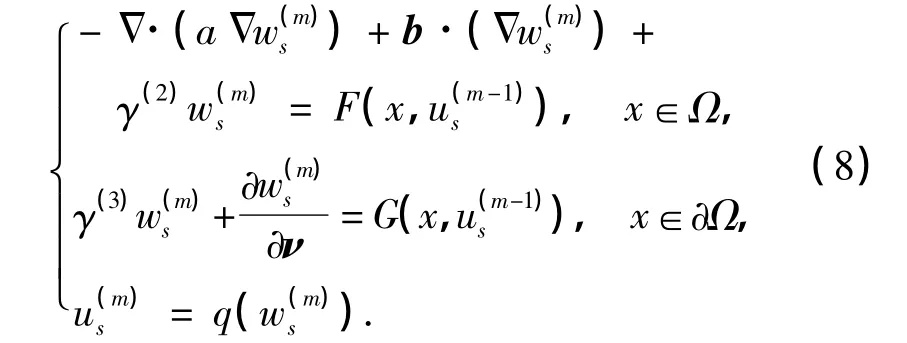
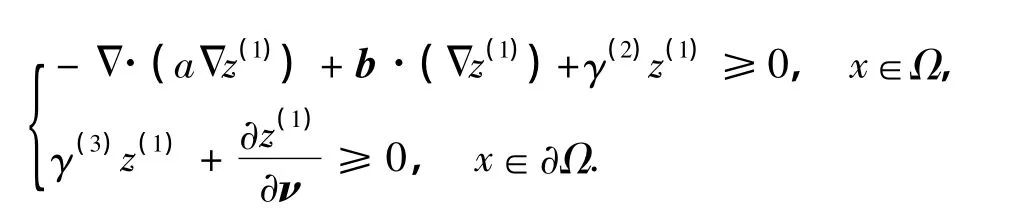
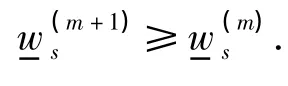
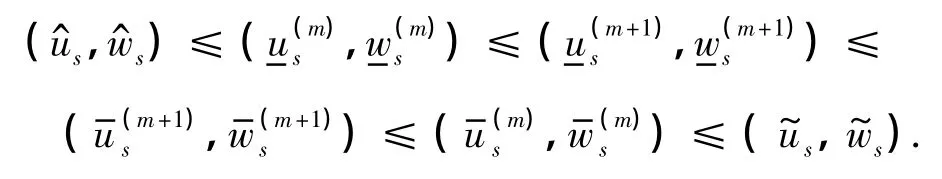
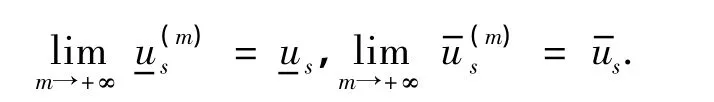
由文献［9］中的引理1.3，有如下估计式：

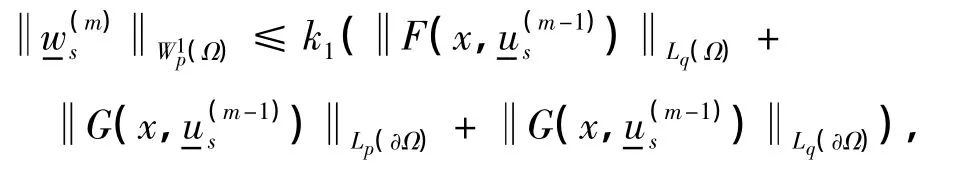
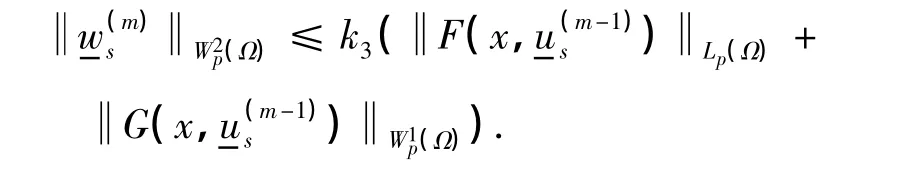
由文献［9］中的定理1.3，可得如下估计式：

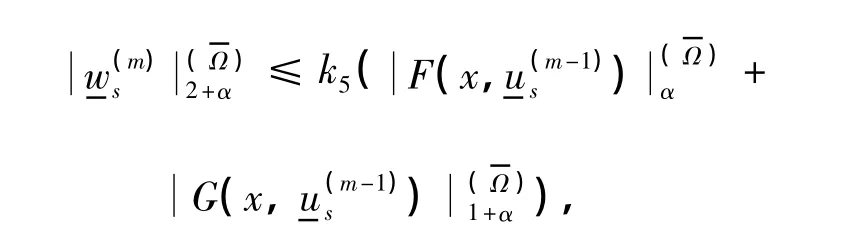
若us∈S0是问题(2)的解，则us既可以看作是问题(2)的上解，又可以看作是问题(2)的下解.当看成上解时，由本定理的前段证明可知，≤us;同理，当看成下解时，可以得到，故可得≤.得证.

3 解的渐近性

定理5 若u0(x)∈S0时，问题(1)的解为u(t，x)，则有

［1］ PAOC V.Quasilinear parabolic and elliptic equations with nonlinear boundary conditions［J］.Nonlinear Analysis，2007，66：639-662.

［2］ PAOC V，RUANW H.Positive solutions of quasi linear parabolic systems with nonlinear boundary conditions［J］.Math Anal Appl，2007，333：472-499.

［3］ DAYW A.A decreasing property ofsolutions of parabolic equation with application to thermoelasticity［J］.Quart Appl Math，1983，40：468-475.

［4］ DENG K.Comparison principleforsomenonlocal problems［J］.Quart Appl Math，1992，50：517-522.

［5］ PAOC V.Dynamics of reaction diffusion equations with nonlocal boundary conditions［J］.Quart Appl Math，1995，53：173-186.

［6］ WANGY L，MUC L，XIANGZ Y.Blowup of solutions to a porous medium equation with nonlocal boundary condition［J］.Applied Mathematics and Computation，2007，192：579-585.

［7］ CUIZ J，YANGZ D.Roles of weight functions to a nonlinear porous medium equation with nonlocal source and nonlocal boundary condition［J］.Math Anal Appl，2008，342：559-570.

［8］ LADYZENSKAJAO A，SOLONNIKOVV A，URAKL’CEVA N N.Linear and quasi-linear equations of parabolic type［M］.Prividence：Amer Math Soc，1968.

［9］ PAOC V.Nonlinear parabolic and elliptic equations［M］.New York：Plenum Press，1992：48-52.

［10］ 吉耳巴格D，塔丁格 N S.二阶椭圆型偏微分方程［M］.叶其孝，译.上海：上海科技出版社，1981.

［11］ 叶其孝，李正元.反应扩散方程引论［M］.北京：科学出版社，1981.