S波段发卡式微带带通滤波器设计

景冻冻， 李国辉， 胡金萍， 官雪辉，2

(1.上海大学特种光纤与光接入网省部共建重点实验室，上海200072; 2.华东交通大学电气与电子工程学院，南昌330013)

随着无线通信技术的快速发展，人类可以利用的频率资源越来越少，因此，对无源电子器件的设计要求也越来越高.研究具有高频率选择性的微波滤波器变得非常有意义，这不仅要求滤波器具有良好的带内性能，而且要有更高的带外性能.良好的带内性能是指插入损耗低、通频带边沿陡峭;带外性能是指良好的谐波抑制能力.传统的微波滤波器频率响应由于分布参数的周期性，在离开主通带一定距离处存在寄生通带，这在频率复用的通信方式中将产生一些相当不利的影响，不适合要求有较高抑制带宽的应用场合.因此，研究设计具有谐波抑制功能的微波滤波器［1-2］，并在此基础上实现陡峭的截止边沿有很强的实际意义.

本研究以发卡谐振器为基础设计带通滤波器，并实现了谐波抑制.传统的发卡谐振器是从平行耦合线的基础上改进而来的，但平行耦合线体积大，受二次谐波的影响也比较严重.在20世纪70年代，Crisatl和Frnakel设计了发卡式滤波器，其基本组成单元是发卡谐振器.发卡谐振器一方面由于结构比较紧凑，减小了尺寸、重量，并降低了成本;另一方面，不需要接地，消除了过地孔引入的误差，具有比平行耦合线滤波器和梳状线交指滤波器更好的电性能，且具有较高的频率稳定度和较低的插入损耗［3-4］.20世纪80年代末，Sagawa等研制出了更加小型化的发卡式滤波器，并将其应用到了微波集成电路中的前端电路部分.近些年，随着加工成本的降低和加工工艺的提高，微带滤波器在平面电路中的应用增多.发卡微带单元的结构通常如下：将半波长的平行耦合微带谐振器变形为U形、类U形或者S形结构，通过改变相邻谐振器之间的耦合方式及耦合度来调节滤波器的性能［5-7］.

1 仿真实例

本研究采用在传统的U形结构(见图1(a))基础上进一步变动得到的类U形谐振器结构(见图1(b)).改进的谐振器结构单元2个分支开路端附近的传输线具有内部耦合线，该特性可以减小滤波器尺寸.相邻谐振器之间的耦合方式有多种，如电耦合、磁耦合、混合耦合，这里采用混合耦合的方式排列5个谐振器单元.2个谐振器之间的间距d和上下偏移距离s决定了二者之间的耦合特性，相邻谐振器之间的耦合系数对滤波器频率特性的影响较大，通过调整d即可改变耦合系数［8-9］.

图1 传统的U形结构和改进的类U形结构Fig.1 Traditional U shape structure and modified U-like shape structure

首先，通过理论计算确定滤波器的具体尺寸以及各个谐振器之间的大致距离、上下偏移的距离;然后，通过电磁仿真软件建立模型，进行仿真.若仿真结果与设计要求误差不大，则可以根据各个参数来微调谐振器之间的距离，以达到理想的设计要求;否则，根据理论重新进行计算、建模、仿真.

谐振器单元的臂长［10］

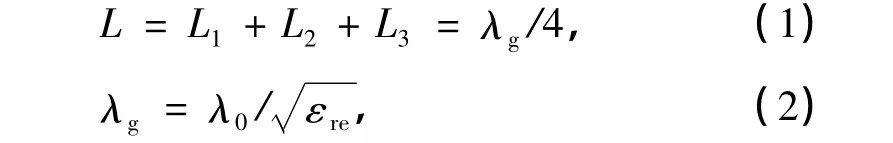
式中，λ0为中心频率在自由空间中对应的波长，εre为介质基片的有效相对介电常数，且

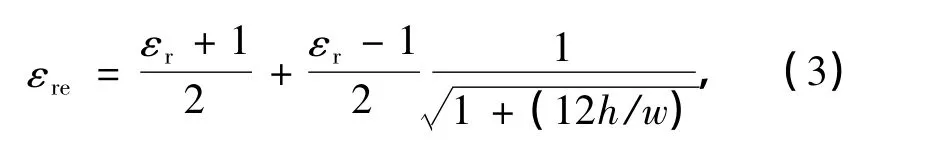
式中，εr为基片的相对介电常数，h为基片厚度，w为微带线宽.

对于级联型滤波器，相邻谐振器间的耦合系数按下式计算：

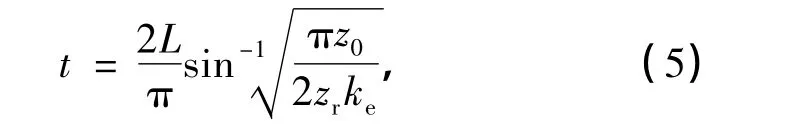
式中，L=λg/4，z0为抽头微带线的特性阻抗，zr为发卡线的特性阻抗，ke为发卡的耦合系数，在此选择特征阻抗z0=50 Ω的微带线作为输入输出微带线.

根据以上理论，通过电磁仿真软件设计得到如图2所示的滤波器结构，其中L1=4.8 mm，L2= 6.0 mm，L3=4.4 mm，L4=2.3 mm，d=0.5 mm，其余微带线宽w=0.5 mm，选用的介质基板的厚度h= 0.5 mm，相对介电常数εr=3.48，中心频率f0约为2.4 GHz，相对带宽为8%，整个滤波器的尺寸约为30 mm×15 mm.

通过电磁仿真软件Sonnet仿真可得出如下结果(见图3)：在通带内S11均小于-15 dB，且在中心频率处达到了-30 dB;该滤波器在通频带的上下频端

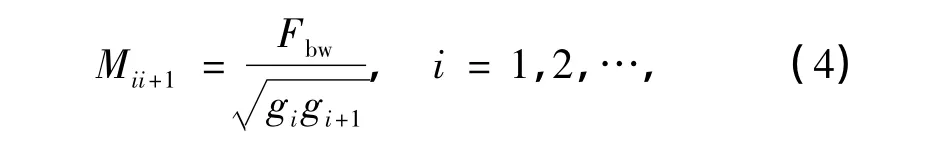
式中，gi为集总参数低通滤波器的原型值，Fbw为相对带宽.

为了在谐振器和馈线之间得到最大的功率转移，激励源与馈线必须匹配，即将谐振器临界耦合到馈线.这里采用抽头式输入输出方式，通过调整抽头微带线到谐振器中间位置的距离t，从而将2个端口对谐振频率的影响减小到最低程度.t一般由如下经验公式来估计：处均插入了传输零点，在 f1=1.74 GHz处 S21＜-128 dB，在f2=2.72 GHz处S21＜-98 dB;同时，在2倍中心频率处将谐波抑制到-60 dB以下，并将二次谐波推移到6.02 GHz处，离开中心频率近3.5 GHz，大大降低了谐波对滤波功能的影响;通带的插入损耗均在3 dB以内，满足应用要求.

图4为不同谐振器间距d对滤波器频率响应特性的影响.图中可以看出，2个相邻谐振器之间的间距影响了传输零点的插入位置.通过比较可得，当d=1.0 mm时，传输零点离通频带边沿最近，阻带特性最好.

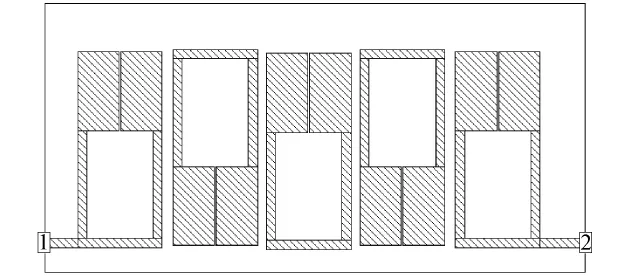
图2 5阶发卡式微带滤波器平面结构Fig.2 Fifth-order hairpin microstrip filter planar structure

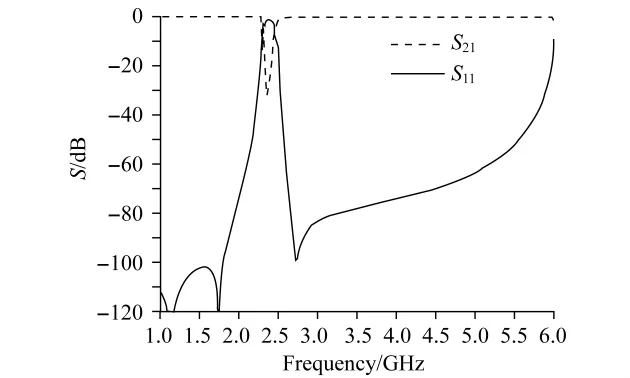
图3 仿真频率响应特性Fig.3 Simulated frequency response

2 实验结果

根据以上仿真结果，选取d=1.0 mm的尺寸进行加工，可得实物如图5所示.

图6为实际加工微带滤波器的频率响应特性测量结果.该结果与前期仿真结果吻合较好，中心频率符合设计要求，基本没有频偏现象，带内回波损耗都在20 dB以上.实测传输损耗与仿真结果比较如图7所示，实测结果带内插入损耗较大，传输零点插入紧凑，阻带性能较仿真结果有一定误差但足以满足应用要求，这些误差主要由介质板的损耗以及微带金属线的辐射损耗造成.实际加工中，通过添加一个金属屏蔽盒，并采用精密的加工技术等可以进一步改善插入损耗［11］.

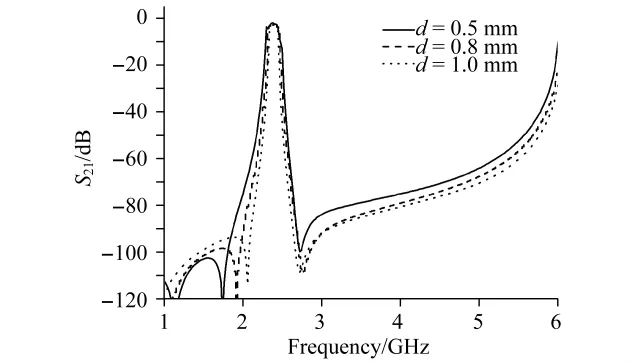
图4 d=0.5，0.8，1.0 mm时的仿真频率响应比较Fig.4 Simulated frequency response for filter d=0.5，0.8，1.0 mm

图5 加工实物图Fig.5 Fabricated filter

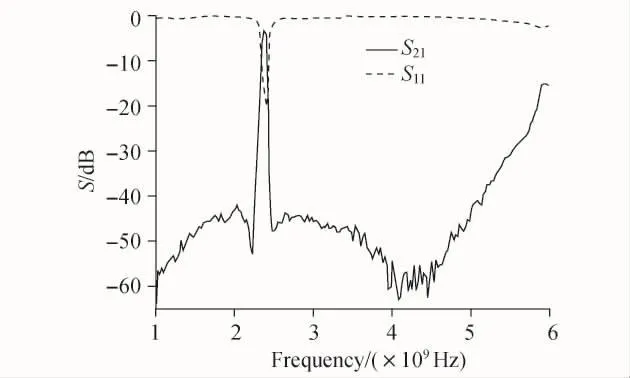
图6 实测滤波器频率响应特性Fig.6 Measured frequency response for filter

3 结束语

本研究设计了一个发卡式微带滤波器，通过仿真设计加工得到的5阶滤波器将二次谐波推向了远离中心频率近3.5 GHz的频段.这不仅实现了谐波抑制的功能，而且在通频带的上下边沿均插入了传输零点，实现了陡峭的截止边沿.所设计的滤波器总体性能优良，可应用于通带过渡到阻带非常陡峭的场合.

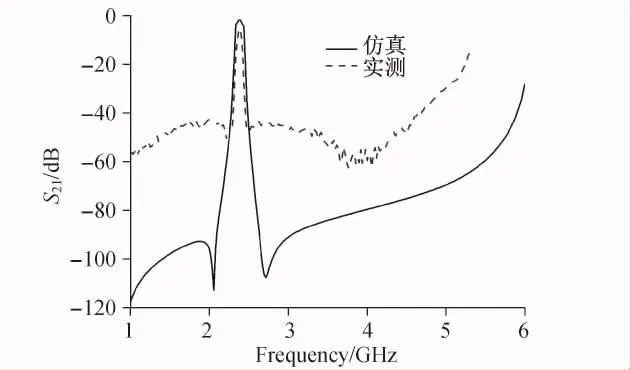
图7 仿真结果与实测结果的比较Fig.7 Comparison between simulated and measured results

［1］ 梁建刚，陈文灵，姜义武.谐波抑制滤波器的计算机辅助设计［J］.现代雷达，2008，30(7)：39-41.

［2］ ZHANGX Y，XUEQ，CHANC，et al.Low-loss frequency-agile bandpass filters with controllable bandwidth and suppressed second harmonic［J］.IEEE Transactions on Microwave Theory and Techniques，2010，59(6)：1557-1564.

［3］ 邓哲，程崇虎，吕文俊，等.微带发夹型谐振器滤波器的实验研究［J］.微波学报，2005，21(S1)：122-126.

［4］ 刘刚，张淑娥.微带交叉耦合发卡式滤波器的设计［J］.华北电力大学学报，2005，32(4)：75-78.

［5］ MARIMUTHUJ，ESAM.Harmonic suppressed single groove PCML bandpass filter［C］∥ Proceeding of the 39th European Microwave Conference.2009：779-782.

［6］ ZHANGX Y，XUEQ.High-selectivity tunable bandpass filters with harmonic suppression［J］.IEEE Transactions on Microwave Theory and Techniques，2010，58(4)：964-969.

［7］ 周春霞，夏侯海，左涛，等.自均衡双通带微带滤波器综合与设计［J］.电子学报，2009，37(12)：2783-2786.

［8］ DIY，GARDERP，HALLP S，et al.Multiple-coupled microstrip hairpin-resonator filter［J］.IEEE Microwave and Wireless Components Letters，2003，13(12)：532-534.

［9］ HONGI，FOKS W，CHOIW W，et al.A novel wigglyline hairpin with 2nd spurious passband suppression［C］∥ Proceeding of the 34th European Microwave Conference.2004：1125-1128.

［10］ TSAIC M，LEES Y，LEEH M.Transmission-line filters with collectivelyloaded coupled lines［J］.IEEE Transactions on Microwave Theory and Techniques，2003，51(5)：1517-1524.

［11］ 严冬，裴旭明，张超，等.基于分形特征的DGS微带传输特性分析［J］.重庆邮电大学学报，2010，22：54-58.