轴向运动Timoshenko固支梁固有频率的数值仿真

张计光， 胡超荣， 唐有绮， 孟沥原

(1.上海大学上海市应用数学和力学研究所，上海200072;2.日照职业技术学院，山东日照276826; 3.同济大学物理系，上海200092)

轴向运动连续体模型广泛存在于军事、航空航天以及机械电子工程等的研究、制造及生产领域，比如空中缆车索道、纸带、升降机缆绳、带锯等.轴向运动梁横向振动及其控制的研究有着重要的应用价值和实际价值.

Euler梁模型是一种简化的、有效的经典模型.许多研究人员分别对轴向运动Euler梁的振动问题进行了一系列的研究［1-5］，但是对于细长的、比较大的梁，Euler梁模型的计算结果远没有Timoshenko模型精确.杨晓东等［6］利用复模态分析方法和Galerkin方法求解轴向运动Timoshenko梁的固有频率，分析复模态分析方法、二阶Galerkin截断和四阶Galerkin截断方法对固有频率结果精确度的影响.Ghayesh等［10］通过半解析半数值方法研究了固定边界的轴向运动Timoshenko梁模型的横向振动固有频率.李彪等［8］通过半解析半数值方法求解了两端非对称混杂边界的轴向运动Timoshenko梁的固有频率.Tang等［9］通过复模态分析方法系统地研究了各种边界的轴向运动Timoshenko梁的固有频率.丁虎等［10］通过有限差分方法研究了简支条件下的轴向运动黏弹性梁的振动问题.本研究利用Galerkin截断方法和微分求积法研究两端固支边界的轴向运动Timoshenko梁的固有频率，并将数值结果和复模态分析方法［9］的结果进行比较.

1 控制方程

轴向运动Timoshenko梁横向振动无量纲形式的控制方程［9］为

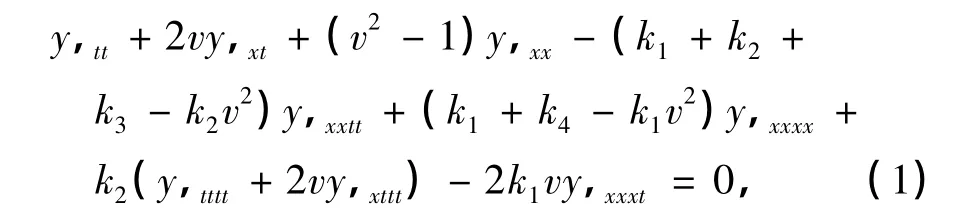
式中，y为运动梁的横向位移，x为梁轴向坐标，t为时间，v为横向速度，k1和k2表征剪切模量的大小，k3表征转角的大小，k4表征抗弯刚度的大小.

两端固支轴向运动 Timoshenko梁的边界条件为

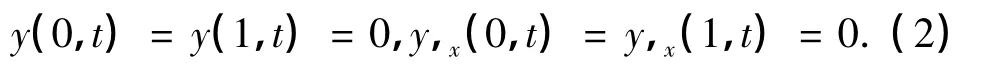
2 数值方法

下面采用Galerkin截断方法和微分求积法对系统进行求解.

2.1 Galerkin方法

利用 Galerkin方法离散，取两端固支的静止Euler梁的模态函数

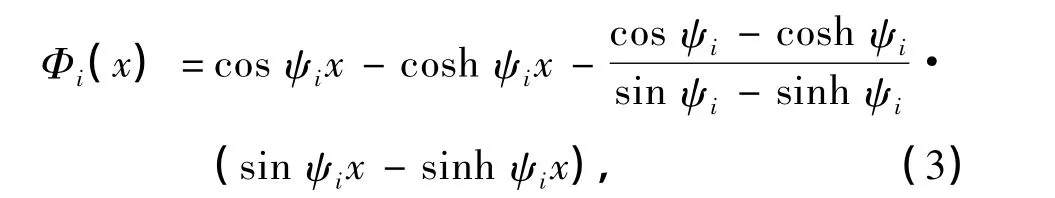
式中，ψi满足cos ψicosh ψi-1=0.

对式(1)运用Galerkin离散化方法，设横向位移的解为 y(x，t)=ΦTq，其中 q=［q1(t)q2(t)…qN(t)］T，Φ=［Φ1(t)Φ2(t)…ΦN(t)］T.将其代入式(1)，然后，等式两端乘以Φ，并在区间［0，1］上对x积分，得

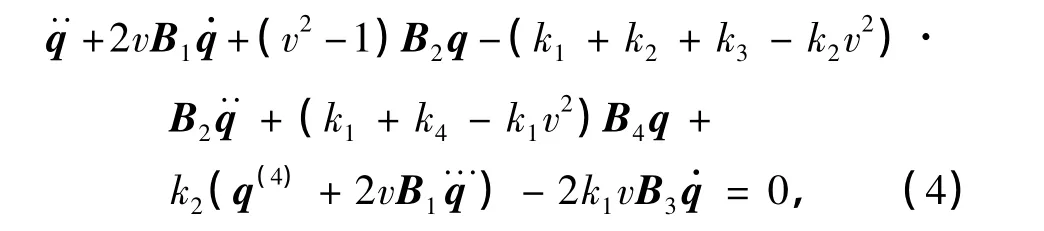
式中，

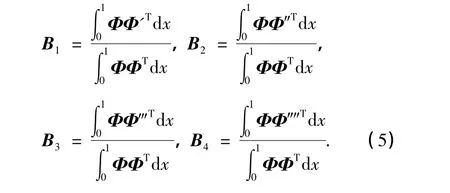
把式(4)写成如下矩阵形式：

其中0和I分别表示N×N的零矩阵和单位矩阵，A为陀螺矩阵，它的全部特征值为成对的虚数，而且存在矩阵T使得如下变换成立：

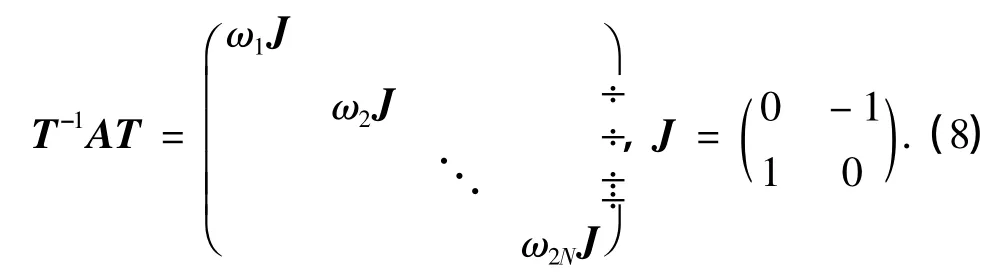
2.2 微分求积法

假设方程(1)的解的形式为

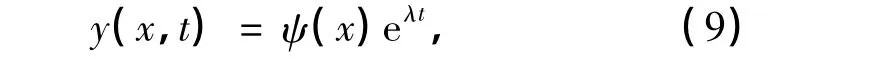
式中，ψ(x)为模态函数，λ为复特征值.

将式(9)代入式(1)和(2)，分别得到

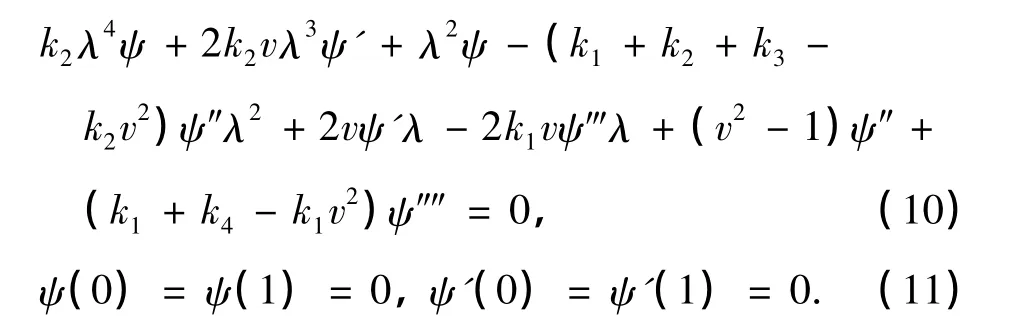
利用δ-technique处理固支边界条件(2)，即采用如下网格节点：

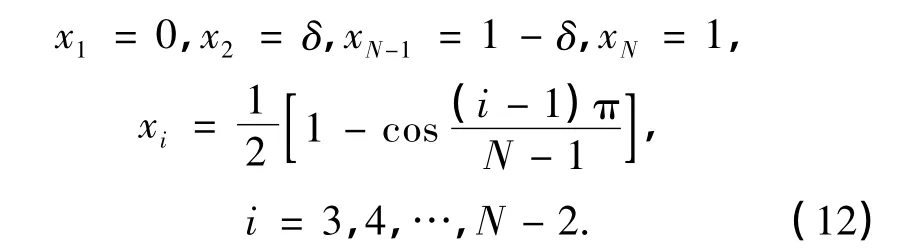
根据微分求积规则：

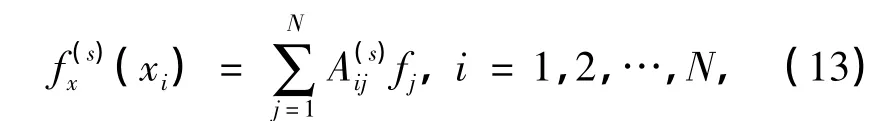
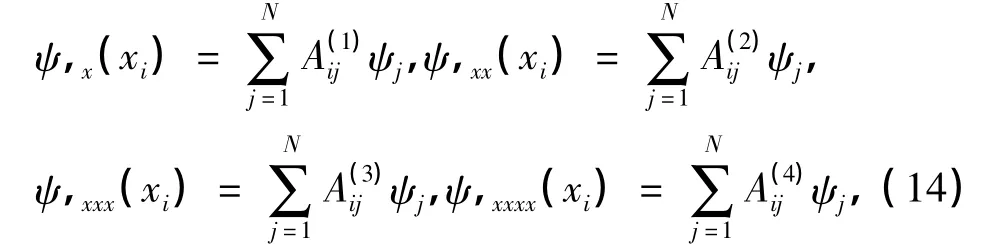
其中的权系数可以由下式确定，即

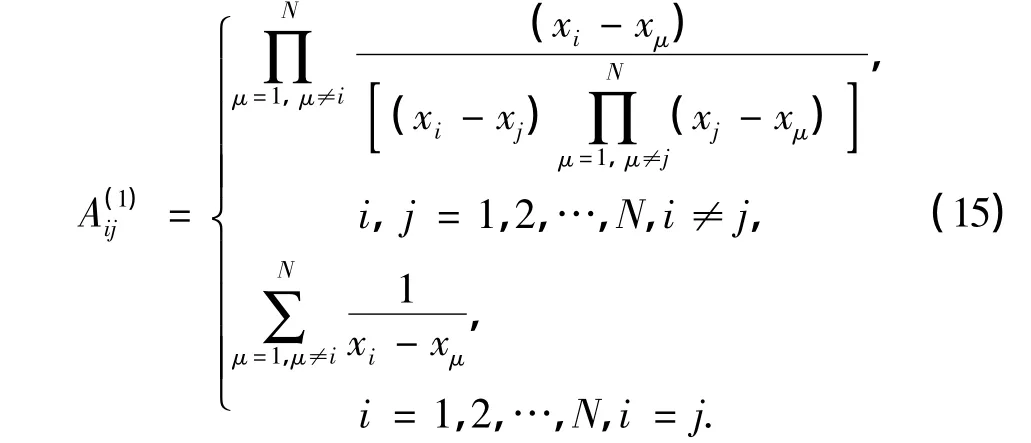
并且当r=2，3，…，N-1时，有

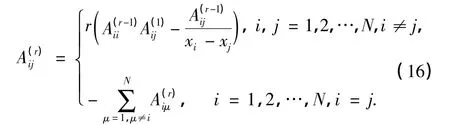
高阶导数的权系数矩阵可以根据表达式 A(r)= A(1)A(r-1)［11］来依次确定.

将式(14)代入式(10)和(11)，可得

将式(17)和(18)转化为矩阵形式，即

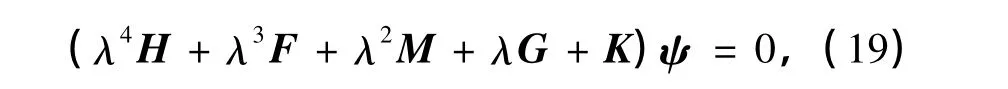
式中，H，F，M，G，K均为N阶矩阵，而ψ为N阶列向量.

方程(19)即为广义特征值求解问题.在本研究的计算中选取11个网格节点，即N=11.

3 计算结果及分析

应用Galerkin方法，由式(11)可以得到轴向运动梁的第n阶固有频率，由式(19)可以用微分求积法得到轴向运动梁的第n阶固有频率.复模态分析法(differential quadrature method，DQM)的解在不考虑计算误差时可以看作精确解;而Galerkin方法因为使用截断必然导致误差的存在.图1(Galerkin方法)和图2(DQM)分别给出了在两端固支的边界条件下Timoshenko模型运动梁在不同刚度时前两阶固有频率随运动梁轴向运动速度的变化情况，其中Timoshenko梁物理参数分别为P=107N，A=9.0× 10-3m2，E=1.69×1011Pa，k=5/6，l=0.3 m，G= 6.6×1010Pa;相应无量化参数k1=9.0×10-3，k2= 5.90×10-5，k3=4.2×10-3，k4=0.64.

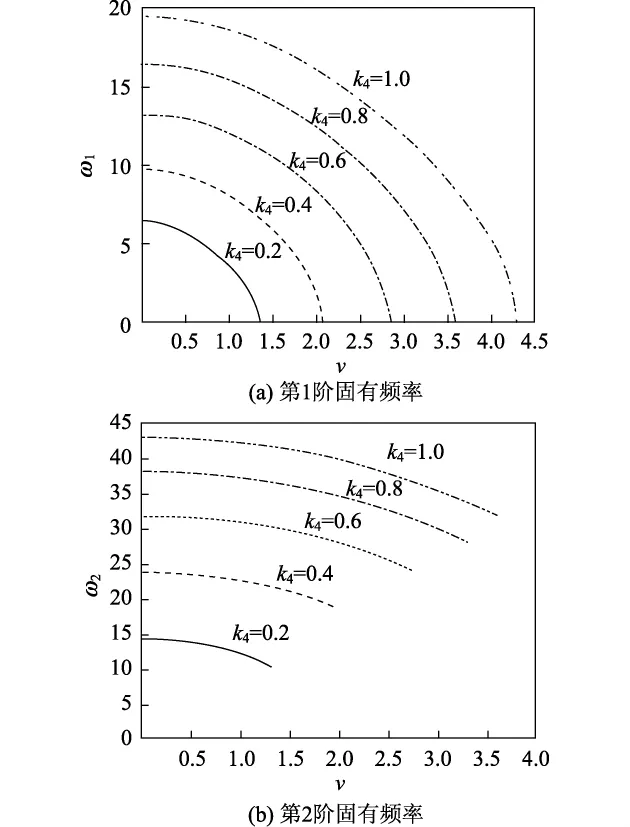
图1 随轴向速度、刚度系数变化的固有频率(Galerkin方法)Fig.1 Natural frequencies changing with axial speed and constraint stiffness(Galerkin method)

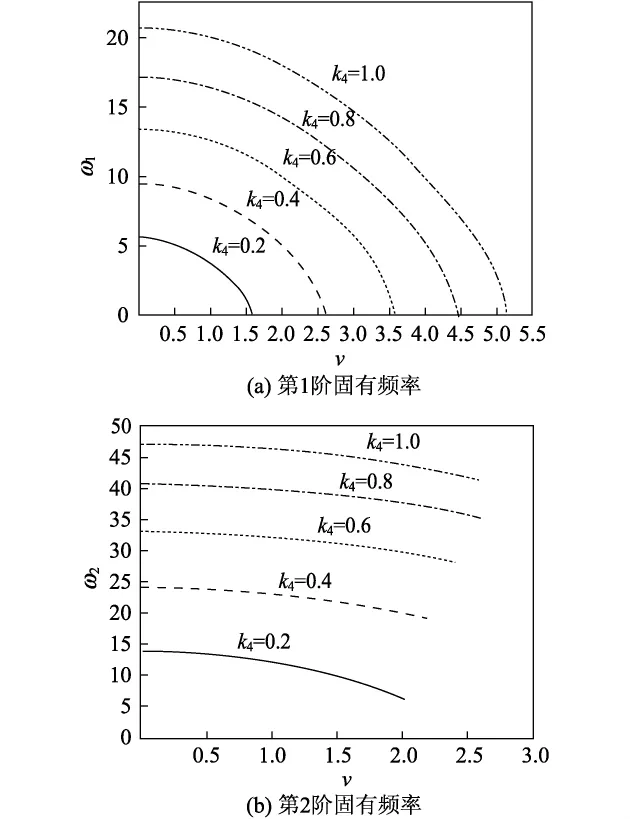
图2 随轴向速度、刚度系数变化的固有频率(DQM)Fig.2 Natural frequencies changing with axial speed and constraint stiffness(DQM)

可以看出，利用Galerkin方法和DQM得到的系统的前两阶固有频率，在轴向速度相同时，随着刚度系数的增大而增大;在刚度系数相同时，随着轴向速度的增大而减小.

图3给出应用Galerkin方法、DQM和复模态分析法［9］所得的固有频率的比较.可以看出，用DQM和复模态分析方法得到的结果吻合得很好;用Galerkin四阶截断法得到的结果与用DQM和复模态分析这两种方法得到的结果存在一定的差别.在刚度系数较小的时候，3种结果比较接近;但随着刚度系数和速度的增大，Galerkin方法的结果和另外2种方法的结果的差别也增大，这种差别应该是由截断的试函数引起的.在两端简支边界条件下，通过利用Galerkin方法和复模态分析法计算出的Timoshenko轴向运动梁的固有频率［6］发现，对第1阶固有频率，用Galerkin方法和复模态分析法计算出的结果几乎重合;对第2阶固有频率，二者虽有差别，但四阶Galerkin截断比二阶Galerkin截断得到的固有频率误差要小.

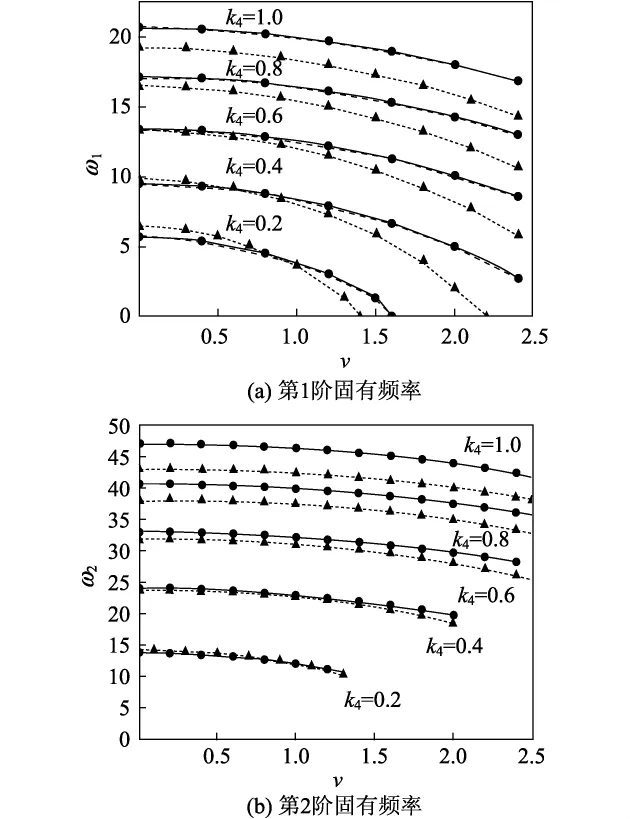
图3 Galerkin方法，DQM，复模态分析法所得固有频率的比较Fig.3 Comparison for the naturalfrequencies of Galerkin method，DQM，complex mode methods

4 结束语

本工作研究了两端固支边界条件下Timoshenko轴向运动梁的横向振动问题，分别利用Galerkin方法和DQM计算了系统的前两阶固有频率随着刚度系数和轴向速度的变化情况，并将这2种方法得到的结果与复模态分析法得到的结果［9］进行比较，发现用DQM和复模态分析方法得到的结果吻合得很好.而用四阶Galerkin截断法得到的结果与用DQM以及复模态分析法得到的结果有着相同的变化趋势，但是存在一定的差别.

［1］ ÖZH R.On the vibrations of an axially traveling beam on fixed supports with variable velocity［J］.Journal of Sound Vibration，2001，239：556-564.

［2］ 冯志华，胡海岩.内共振条件下直线运动梁的动力稳定性［J］.力学学报，2002，34：389-400.

［3］ 陈树辉，黄建亮.轴向运动梁非线性振动内共振研究［J］.力学学报，2005，37：57-63.

［4］ 张伟，温洪波，姚明辉.黏弹性传动带1∶3内共振时的周期和混沌运动［J］.力学学报，2004，36：443-454.

［5］ CHENL Q，WANGB.Stability of axially accelerating viscoelastic beams：asymptotic perturbation analysis and differential quadrature validation［J］.European Journal of Mechanics A/Solids，2009，28：786-791.

［6］ 杨晓东，唐有绮，戈新生.轴向运动Timoshenko梁固有频率的求解方法研究［J］.机械强度，2009，31(2)：208-210.

［7］ GHAYESHM H，BALARS.Non-linearparametric vibration and stability analysis for two dynamic models of axially moving Timoshenko beams［J］. Applied Mathematical Modelling，2010，34：2850-2859.

［8］ 李彪，丁虎，陈立群.非对称混杂边界轴向运动Timoshenko梁横向振动分析［J］.固体力学学报，2009，30(6)：565-570.

［9］ TANGYQ，CHENLQ，YANGX D.Natural frequencies，modes and critical speeds of axially moving Timoshenko beams with different boundary conditions［J］.International Journal of Mechanical Sciences，2008，50：1448-1458.

［10］ 丁虎，陈立群.轴向运动黏弹性梁平面耦合非线性受迫振动［J］.上海大学学报：自然科学版，2009，15(6)：649-652.

［11］ MALINK M， BERT C W. Implementingmultiple boundary conditions in the DQ solution of higher-order PDE’s：application to free vibration of plates［J］.International Journal for Numerical Methods in Engineering，1996，39：1237-1258.