基于小波的肿瘤基因表达数据聚类分析模型

黄文佳， 冯铁男， 王翼飞

(上海大学理学院，上海200444)

基因芯片(gene chips)是目前最主要的且发展最早、最快的生物芯片［1］.将待测样本标记后与基因芯片进行杂交，经激光共聚焦荧光扫描仪扫描，通过电脑系统处理、分析即可得到相应的信号值.信号值代表了结合在探针上的待测样本中特定大分子的信息，从而可检测对应片段是否存在及存在量的多少.狭义的基因芯片又叫DNA微阵列(DNA microarray)，主要包括cDNA微阵列和寡核苷酸微阵列.

DNA芯片技术作为一种高通量的基因表达分析平台，通过一次试验就能获得成千上万个基因的表达数据，该技术已被广泛应用于生物医学、疾病诊断和药物筛选等多个领域［2］.由于基因表达的信号值常常受到噪音的污染，而传统的研究方法无法将其去除，因此经常在发现特异表达基因时出现较高的假阳性，降低了样本聚类的准确率，并且对研究基因表达模式、提取分类特征基因等带来了一定的困难.

小波变换(wavelet transformation)是空间(时间)和频率的局部变换，因而能有效地从信号中提取信息，通过伸缩和平移等运算功能，可对函数或信号进行多尺度的细化分析，特别适用于非稳定信号的信息提取［3］.

为解决聚类过程中存在的一些问题，本研究通过对基因表达数据进行小波变换，降低表达值中的噪音，从而为提取出基本信息建立了一种新的聚类分析模型.通过该模型选取的特异表达基因，对于肿瘤样本的分类、肿瘤疾病的诊断和治疗都具有重要意义.

1 聚类分析模型

1.1 传统的肿瘤聚类分析模型

肿瘤聚类分析模型［4］假设具有相同或相似表达模式的基因功能相同或相近，因此通过聚类分析可以将基因分为不同的类型，同时选取出少量的特异表达基因对样本进行聚类.

肿瘤聚类分析模型的主要流程如下：①获取基因表达数据，并对数据进行预处理和归一化;② 依次计算每个基因的综合属性，将每个基因在不同样本中的表达值转化为一个数值;③选取少量的特异表达基因，选择一种聚类分析方法对基因和样本分别进行聚类，将表达模式相似的基因聚为一类，这些基因可能具有相同或相似的功能.通过对样本聚类，可以将正常样本聚为一类或将疾病样本聚为一类，也可将疾病样本分为不同的疾病亚型，这将为进一步深入研究肿瘤疾病提供重要的信息.

1.2 改进的聚类分析模型

传统的肿瘤聚类分析模型由于芯片的背景噪音等常会产生假阳性，导致较高的错聚率.本研究建立了一种改进的聚类分析模型(见图1)，其创新点在于运用小波变换的方法来降低噪音.通过小波变换，可以有效去除假阳性的差异表达基因，从而降低样本的错聚率.这里的错聚率是指聚到错误类别的样本个数占样本总数的比率.

1.2.1 基因排序

对基因表达数据集的每一行(即一个基因在不同样本中的表达值)进行逐个记分，得分越高则基因的差异表达程度越高.将基因按照记分高低排序，挑选得分高的基因作为特异表达基因.

图1 肿瘤基因表达数据聚类分析模型Fig.1 Cluster analysis model of tumor gene expression data

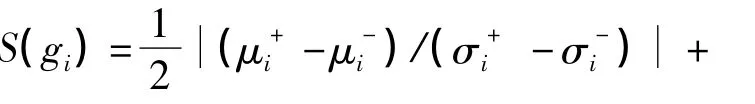
1.2.2 耦合双向聚类

耦合双向聚 类(coupled two-way clustering，CTWC)是Getz等［7］提出的一种无监督聚类框架.该聚类方法是一个迭代的过程，通过采用启发式的方法寻找由稳定的样本簇和基因簇构成的子矩阵，从而得到稳定的聚类结果.该方法动态地利用了样本簇和基因簇之间的关系，交替地使用基因簇作为特征聚类样本或者使用样本簇作为特征聚类基因，最终得到生物学上相关的基因聚类簇和样本聚类簇［8］.

本研究选定的错聚率阈值为15%.若样本聚类的错聚率低于阈值，说明该数据集存在的噪音不大，无需进行小波变换来降低噪音;若高于阈值，说明该数据集存在较大的噪音，需要通过小波变换来降低噪音.

1.2.3 小波变换

若基因表达数据存在较大的噪音，则需采用一种科学的数据处理方法来降低噪音.小波变换作为近年来信号去噪的一个有力工具，能以非常小的失真度实现对信号的压缩与消噪［9］，其表达式为C(scale，time_position)=∫f(τ)Ψ(scale，τ)dτ.通过小波变换，信号可以被分解为高频部分和低频部分.对于被噪音污染的信号，小波将其分解为代表近似信号特征的低频部分和代表噪音及扰动的高频部分［4，10］.

本研究采用双正交小波3.3(biorthogonal wavelet 3.3)进行3个层次的离散小波变换(见图2).通常经小波变换后，信号的噪音可被有效地降低.小波将该信号值进行了3层分解，即

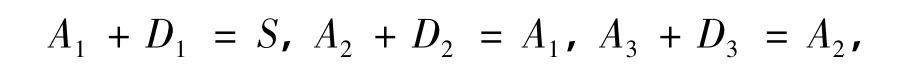
其中A1层保留了信号的基本特征，A2和A3层只保留了少量的低频信号，D1，D2和D3层包含了原始信号在不同层次下的噪音及扰动信号.本研究选用A1层近似表示基因的原始信号值并对其进行分析.

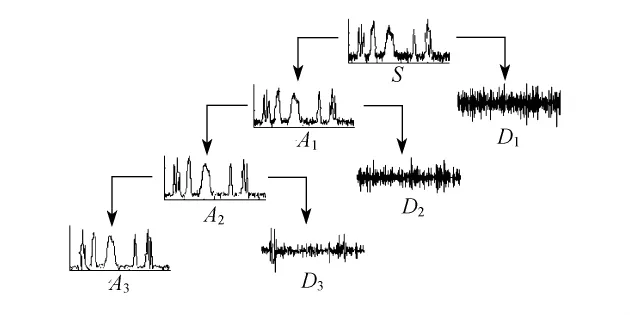
图2 对原始信号进行3个层次的离散小波变换Fig.2 Using discrete wavelet to transform the original signal at level 3

1.2.4 剔除相关性强的基因

由于通过RFSC筛选出的特异表达基因中可能存在功能相同或相似的基因，即存在一定的冗余基因;而从生物学的角度分析，基因之间存在调控和相互作用，这在表达谱中反映为不同基因在表达水平上存在一定程度的相关性［4］，据此可以进行冗余基因的排除.

算法的主要步骤如下：①计算特异表达基因两两之间的相关系数，若有n个特异表达基因，则计算n(n+1)/2次;②对计算出的基因两两之间的相关系数进行排序，挑选出相关系数最高的2个基因，剔除得分较低的基因;③ 再次进行聚类，当样本错聚率高于阈值时，返回到步骤②，当样本错聚率低于阈值时，停止;④找出样本错聚率达到最低时的最少基因数目，将这些基因作为特异表达基因.

第i和第j个基因的相关系数的计算公式为

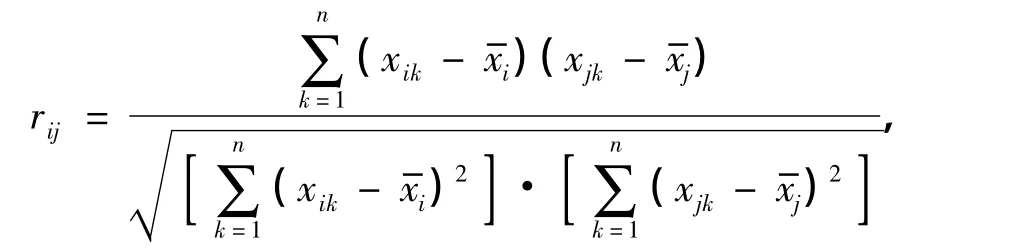
当i=j时，基因的自相关系数rij=1;当i≠j时，rij的取值在0～1之间.

2 应用算例

2.1 材料

本研究以肿瘤基因表达谱为研究对象，选取Alon等［11］公布的结肠癌基因表达数据集作为分析数据.该数据包含62个样本(数据的下载地址为http：//microarray.princeton.edu/oncology/affydata/ index.html)，每个样本均含2 000个基因的表达数据，其中40个样本被诊断为结肠癌(Tumor)，其余22个样本为正常样本(Normal).

2.2 分析过程与结果

本研究以上述结肠癌基因表达数据集为例来进行实际分析.通过RFSC对结肠癌数据集的每个基因进行打分，从2 000个基因中挑选出39个得分最高的特异表达基因.

2.2.1 选取特征基因

对39个结肠癌特异表达基因及62个样本进行耦合双向聚类，得到的样本聚类图如图3所示，其中图3(a)由未经小波处理挑选出的特异表达基因聚类得到，样本错聚率达到33.87%，图3(b)由经过小波处理后挑选出的特异表达基因聚类得到，样本错聚率为11.29%.由图可见，通过小波处理有效地降低了原始信号的噪音以及样本的错聚率，对比之前未经小波变换处理的原始信号，处理后的信号通过耦合双向聚类得到了更好的效果.

图3 耦合双向聚类得到的结肠癌样本聚类图Fig.3 Cluster tree of colon samples through CTWC

2.2.2 剔除假阳性基因

经过小波变换后，部分假阳性基因被有效剔除.探针号为R99907的基因在未经小波变换处理之前被判定为特异表达基因，但通过小波变换对该基因的信号值进行2层分解(见图4)后，该基因被认定为冗余基因而被剔除.从图4可以看出，有一个正常样本的表达值达到了2 029.322，远远高于其他19个正常样本的平均表达值70.186.假设该样本与其他样本存在显著差异，通过 t-检验得出该样本(Normal-11)的p-value为5.588 6E-020(当p-value＜0.05，拒绝假设)，因此该样本与其他正常样本不存在显著差异，是一个被噪音污染的基因.另外，通过查询NCBI数据库可知，该基因为干扰素调节因子-2，是转录因子基因家族中的一员，其基因符号为IRF2.IRF2竞争性抑制IRF1介导转录激活的干扰素α和β，还具有组蛋白H4的转录激活因子的作用，但通过查询结肠癌的基因调控通路，目前暂时还没有发现该基因与结肠癌的发生有直接的联系.

图4 探针号为R99907的基因原始信号的小波多尺度分解图Fig.4 Wavelet multiresolution decomposition of original signal of gene R99907

2.2.3 聚类结果分析

本研究通过建立一种聚类分析模型来分析结肠癌数据集.采用小波变换对表达信号值降噪，剔除了结肠癌特异表达基因中相关性强的基因，并从筛选出的39个特异表达基因中剔除了12个冗余基因，从中挑选出27个特异表达基因(见表1).通过对这27个特异表达基因及62个样本进行耦合双向聚类，样本的错聚率为8.06%.聚类效果如图5所示，图中的第1～25行被聚为Normal类，第26～62行被聚为Tumor类.特异表达基因被聚为4类：第1～17列的基因被聚为1，2类，这2类基因在肿瘤样本中相对下调表达;第18～27列被聚为3，4类，这2类基因在肿瘤样本中相对上调表达.Alon等［11］提出可以依靠数量更少的基因对样本进行聚类，并选出了500个基因进行实验，得到了较低的错聚率.通过对比几种不同的聚类模型(见表2)可知，改进的聚类分析模型不但降低了样本的错聚率，也减少了对样本进行聚类的基因数量，改进后的肿瘤聚类分析模型取得了较好的效果.

2.2.4 关于肿瘤基因表达谱的分析结果

(1)样本聚类结果.

62个样本聚类结果表明，所有样本分类基本准确，其中正类样本(Normal)的错聚率为4.54%，负类样本(Tumor)的错聚率为10.00%，总的样本错聚率为8.54%.

(2)特异表达基因.

根据分析结果可知，27个基因在结肠癌中差异表达，其中17个基因在结肠癌样本中相对下调表达;10个基因相对上调表达.在结肠癌中下调表达的基因主要有：细胞功能调控相关基因CRSP1;蛋白质调控相关基因CDH3，CKS1B;蛋白质编码相关基因DES，MYL9，CLNS1A;核糖蛋白合成相关基因SND1;细胞通讯相关基因 ITGA6，转录相关基因FBL.下调表达的基因主要有：核酸和蛋白质绑定功能、转录因子激活功能的基因PABPC1;离子膜转运功能基因PLP2;编码免疫蛋白的相关基因HSPD1;调节酶活性的相关基因ACHY.

本研究通过改进的聚类分析模型所发现的27个特异表达基因在结肠癌中保持差异表达，因此，可以推断这些基因在正常组织癌变的过程中所起到的重要作用，与结肠癌的发生可能存在着密切的联系.

表1 结肠癌数据集的特异表达基因Table 1 Specific expressed genes of colon tumor dataset

图5 27个基因的耦合双向聚类效果图Fig.5 Cluster of 27 genes through CTWC

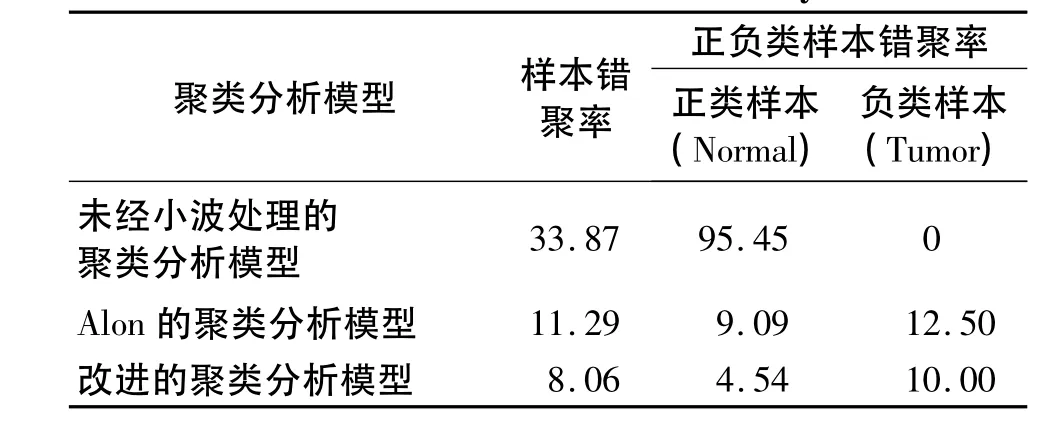
表2 几种不同聚类分析模型的结果对比Table 2 Results contrast of different cluster analysis models %

3 结束语

近年来，研究基因表达数据的方法层出不穷，但对于如何从大量基因中剔除冗余基因、去除表达信号中的噪音仍然是研究的难题.本研究针对肿瘤基因数据的聚类问题所建立的模型只需提取少量的基因就能用于肿瘤样本的聚类.但是在进行小波变换去噪的过程中也可能将某些有意义的基因剔除，如果能够构造一种专门用于给基因表达数据去噪的小波，将有助于该模型成为基因表达数据分析的有力工具.

［1］ 王翼飞，史定华.生物信息学——智能化算法及其应用［M］.北京：化学工业出版社，2006：221-243.

［2］ 李瑶.基因芯片数据分析与处理［M］.北京：化学工业出版社，2006：162-180.

［3］ 飞思科技产品研发中心.MATLAB6.5辅助小波分析和应用［M］.北京：电子工业出版社，2003：151-184.

［4］ 王树林.基于基因表达谱的肿瘤分类研究进展［M］∥黄德双，刘海燕，施蕴渝，等.生物信息学中的智能计算理论与方法研究.合肥：中国科学技术大学出版社，2007：56-64.

［5］ GOLUBT R，SLONIMD K，TAMAPYOP，et al.Molecular classification of cancer：class discovery and class prediction by gene expression monitoring［J］.Science，1999，286(5439)：531-537.

［6］ FUREYT S，CRISTIANININ，DUFFYN，et al.Support vector machine classification and validation of cancer tissue samples using microarray expression data［J］.Bioinformatics，2000，16(10)：906-914.

［7］ GETZG，LEVINEE，DOMANYE.Coupled two-way clustering analysis of gene microarray data［J］.PNAS，2000，97(22)：12079-12084.

［8］ 赵宇海，王国仁，印莹.一种用于基因表达数据的无参数聚类算法［J］.计算机应用，2005，25(6)：1388-1391.

［9］ 冉启文，谭立英.小波分析与傅里叶变换及应用［M］.北京：国防工业出版社，2002：52-87.

［10］ RAINERK，GUNNARS，MARCUSO，et al.Discovering functional gene expression patterns in the metabolic network of Escherichia coli with wavelets transforms［J］.BMC Bioinformatics，2006，7：119-132.

［11］ ALONU，BARKAIN，NOTTERMAND A，et al.Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays［J］.Proc Nat Acad Sci USA，1999，96(12)：6745-6750.