考虑预期效应和交通灯影响的城市道路交通元胞自动机模型

张 剑， 董力耘

(上海大学上海市应用数学和力学研究所，上海200072)

随着大中城市机动车保有数量的不断增加，机动车排放的尾气已经成为城市环境的主要污染源，而日益严重的交通堵塞，更加剧了城区机动车的尾气污染.众所周知，机动车的尾气排放与车辆的运行状态密切相关，频繁加速或减速以及长时间处于怠速状态都会导致额外的污染物排放［1］.为了更加真实地评估机动车流的尾气排放，进而实现节能减排，必须采用可以描述每辆机动车具体运动过程的交通流微观动力学模型，其中元胞自动机模型已于近几年开始应用于交通流的模拟，并因其简单、灵活和适于大规模并行计算的优势而得到普遍重视.

1992年，Nagel等［2］提出了一个描述高速公路交通的单车道元胞自动机交通流模型，即NaSch模型.该模型是一个可以重现道路交通流基本特征(如自由流和阻塞相及其相变)的最简单的模型.国内外很多学者在NaSch模型的基础上不断进行研究和改进，先后涌现出大量的后续研究成果，其中值得关注的模型有：通过引入慢启动规则再现亚稳态和回滞现象的模型，如VDR模型［3］;可以再现同步流的模型，如Knospe等［4］提出的考虑刹车灯影响和预期效应的BL模型(又称舒适驾驶模型、CD模型).这些研究工作使人们对于高速公路交通流的自组织演化有了更加深刻的认识.

与高速公路交通流相比，有关城市道路交通流的研究相对较少.一方面，城市道路交叉口处的交通灯严重干扰了交通流的自组织行为，很难产生同步流现象;另一方面，交通灯在交叉口处从时间上将原本相互冲突的交通流分离，使其在不同的时间范围内通过交叉口，从而保证了车辆在交叉口的行驶安全.Biham等［5］提出了一个理想化的二维元胞自动机模型，即BML(Biham-Middleton-Levine)模型，它采用一个二维正方形网格来表示城市交通网络，每一格点代表一个交叉路口，车辆在交通灯的控制下向前运动.BML模型只能用来模拟城市交通的一些基本特征，如超过临界密度会发生全局的阻塞.由于BML模型过于简单，无法刻画一些实际的交通特征，为了解决这一问题，Chowdhury等［6］将BML模型和NaSch模型相结合，建立了一个新的ChSch模型来刻画城市交通.ChSch模型考虑了连接路口之间路段上的交通流动力学演化过程，较为真实地描述了实际交通.距离交叉口最近的车辆考虑交通灯的影响，并据此作出相应的预判.Brockfeld等［7］采用元胞自动机模型研究了城市交通的交通灯信号优化问题，指出交通灯控制下的城市交通流可以简化为单车道的问题.Sasaki等［8］采用优化速度模型研究单车道情况下交通灯控制下的交通流.He等［9］也采用元胞自动机模型对同步、绿波、随机三种交通灯控制策略下的交通流进行了模拟，结果显示，低密度下绿波控制策略是有效的，但高密度下三种控制策略并无差别.Jiang等［10］提出了一个随机减速概率依赖于停车时间的元胞自动机模型.刘慕仁等［11］在研究城市道路交通问题与交通流模型时指出，交通系统是一个人、车、路和环境构成的复杂巨系统，系统参数的数量和变化范围很大.因此，到目前为止还没有一个统一的模型能描述和解释各种实际交通流复杂行为，要建立一个统一的交通流模型还需要进行更多的研究工作.

本工作主要关注交通灯控制下城市道路交通流的动力学演化过程，重点研究机动车的微观运动状态，如加速、减速和怠速，这些状态与机动车的尾气排放过程直接相关.本工作提出了一个新的模型，其中交通灯状态不但对距离路口最近的车辆产生直接的影响，同时也会影响到其他车辆的运动.通过与ChSch模型比较，进一步说明了本工作所提出模型的合理性，并且重点分析了机动车流运动状态与尾气排放之间的联系.

1 模型

在文献［4，7］的基础上，本工作提出了一个新的描述交通灯控制下单车道机动车流演化的元胞自动机(traffic-light-based cellular automaton，TLCA)模型.在该模型中，首先考虑交通灯状态对当前路段上所有车辆的影响，对于最靠近前方路口的车辆(称为头车)的运动，则根据实际情况作相应的处理，具体规则如下.

(1)确定车道上各辆车的加速度.① 对于头车，先确定头车的控制速度vcon.当前方交通灯为红灯时，vcon=min(ceil(sl/τ)，vmax)，其中ceil为上取整函数，sl为头车到前方最近路口的距离;当前方交通灯为绿灯时，vcon=vmax，则头车的加速度为

式中，vl为头车的当前速度，τ为红灯状态的剩余时间长度.②对于其他车辆，

式中，vn表示第n辆车的速度，dn表示第n辆车和前车(第n-1辆车)之间的间距，即dn=xn-1-xnln-1，其中xn为第n辆车的位置，ln-1为第n-1辆车的车长，k为交通灯状态对驾驶员行为的影响参数，当红灯时，k=1，当绿灯时，k=2，表明绿灯期间驾驶员更倾向于向前行驶.对于加速或减速的判断可借鉴文献［2］中的方法，该方法可较为真实地反映运动中两车之间间距的变化.

(2)速度调整.由

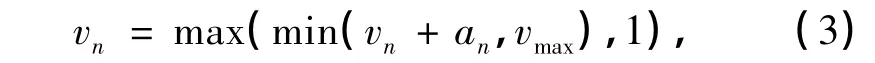
驾驶员可根据步骤(1)确定的加速度调整速度(加速或减速).这一步中始终保持vn≥1，反映了驾驶员尽可能保持行驶状态的心理.

(3)由交通灯状态引起的减速.如果第n辆车前方是红灯，则有

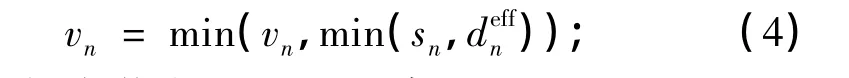
如果第n辆车前方是绿灯，则有

式中，sn表示第 n 辆车到前方最近路口的距离，=d+max(v-gap，0)表示有效间距，其中nantisecurityvanti=min(dn-1，vn-1)为前车的期望速度，gapsecurity为安全控制参数，为了防止前后车碰撞，要求gapsecurity≥1.本模型使用有效间距来替代真实的车间距，可放松NaSch模型中间距对车辆运动的限制，通过合理选择参数，保证了当间距较小时不至于发生碰撞.

(4)随机减速.以随机减速概率P减速，即速度取为

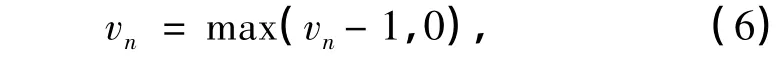
反映驾驶过程中各种不确定因素的影响.(5)根据确定的速度

车辆向前运动.

本工作提出的TLCA模型较为全面地考虑了交通灯对车辆运动的影响，这种影响不仅通过头车运动的变化来传递，还直接作用于车道上其他所有的车辆.这是因为在大部分情况下，即使在车队尾部的驾驶员也可以明确获得当前交通灯的信息而做出相应的调整，这与ChSch模型中的处理方式有明显的不同.

2 模拟和分析

在模拟中，每个元胞长度取为1.5 m，每一时间步对应的真实时间为1 s.每辆车占5个元胞(即7.5 m)，单位速度为 5.4 km/h，单位加速度为1.5 m/s2.与NaSch和ChSch模型相比，本模型采用了更小的元胞长度，可以更好地刻画速度的变化过程，从而更准确地描述机动车尾气的排放特征.车道由1 000个元胞组成，即道路长为1 500 m，随机减速概率P=0.12.在道路右端设置交通灯，使用周期性边界条件，相当于采用同步交通灯控制策略.车辆在道路上自左向右行驶，且在行驶过程中不允许超车.由于城市中车辆的最大行驶速度远低于高速公路，因此，假设最大车速为vmax=81 km/h=15 cell/s.如果车头已经越过路口，即使是红灯状态，头车仍旧向前行驶.为简便起见，假设每个信号周期仅由绿灯和红灯组成，且红绿灯周期相同，交替切换，即Tgreen= Tred=T/2分别为交通灯的绿(红)灯周期，其中T为一个交通灯周期长度，在模拟中一般取T=120 s.下面比较TLCA模型与细化的NaSch模型(FNS，指考虑交通灯影响而不考虑预期效应的NaSch模型)和细化的ChSch模型(FCS)的模拟结果，这里的细化是指采用了比原模型更小的元胞长度.

模型的基本图，即流量-密度曲线，反映了交通灯控制下交通流状态的宏观统计特征(见图1).可以发现，3个模型的基本图具有类似特征，整个密度范围可以分成3个区间，分别对应于未饱和、饱和与过饱和状态.在饱和状态时形成了一个流量平台，流量平台的起点和终点分别对应于临界密度ρc1和ρc2.在未饱和状态，系统尚未达到最大通行能力，流量随着密度的增加线性增长.当密度增加到ρc1时，系统达到其最大通行能力，路口上游的车辆无法在绿灯周期内消散.随着密度的不断增加，拥堵范围不断扩大，流量值不再随着密度的增加而增长，而保持在一个固定值，从而出现了一个流量平台.系统的饱和流量取决于最大速度、随机减速概率和交通灯信号周期.当密度超过ρc2时，前方路段已经没有足够的空间容纳上游来流，从而出现流量随着密度的增加而减小.

图1 3个模型的基本图(流量-密度曲线)Fig.1 Fundamental diagram for three models(flowdensity relation)

值得注意的是，FNS模型与FCS模型的基本图几乎完全重合，这是由于FCS模型只考虑头车是否能在有限的绿灯时间内通过交叉口来进行判断，交通灯的影响仅通过头车运动的变化来传递，因此，与完全未考虑交通灯变化预期的FNS模型没有显著的差异.进一步分析表明，FNS模型和FCS模型在微观特征上也几乎完全一致.因此，下面仅对FCS模型与TLCA模型的结果进行比较.

从图2中可看出，ρc1随着交通灯周期的增加而增大;而ρc2则刚好相反，随着交通灯周期的增加而减小.这就导致了基本图中的平台宽度随着周期的增加而减小，如图3所示.从图4中可以发现，随着信号灯周期的增加，平台流量不断提高.这是由于当信号周期比较短时，交通灯的快速切换使车辆频繁启动和刹车，单位时间内通过的车辆减少，交叉口流量降低;而随着信号灯周期的增加，车辆频繁启动的次数降低，车流量增加.

图2 临界密度与信号灯周期关系曲线Fig.2 Relation between critical density and cycle time of signals

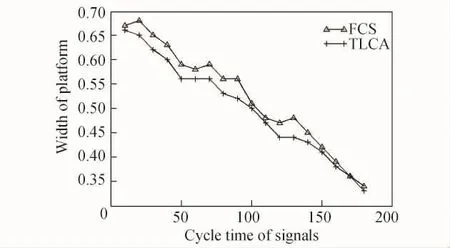
图3 平台宽度与信号灯周期关系Fig.3 Relation between the width of platform and cycle time of signals

图4 平台流量与信号灯周期关系Fig.4 Relation between saturated flux and cycle time of signals

随着信号灯周期的增加，平台宽度变窄而流量值提高，因此，可以根据道路的实际车辆密度来调整信号灯周期长度.虽然增加周期长度有助于提高平台流量，但是周期过长会增加驾驶员的等待时间，容易引起驾驶员的烦躁从而导致不必要的交通事故.

图5为典型密度下FCS模型和TLCA模型的时空演化斑图(车辆从左向右行驶).由图可见，两种模型下车辆运动轨迹表现出了显著不同的特征.在FCS模型中，因为车辆遇到红灯时并不进行预先减速，红灯状态下当车辆到达交叉口时车辆必须进行紧急停车，从高速行驶状态转变为静止状态，因此，可能发生在单位时间步内车速从最大速度骤减为0的情况.而在TLCA模型中，很难发现这种情况.这是由于在TLCA模型中充分考虑到了驾驶员的预判行为，当前方信号灯为红灯时，头车驾驶员会根据红灯周期剩余时间和该车辆到路口之间的距离来改变速度，其后车辆也会随之进行相应的调整.

图6为典型密度下两种模型的速度分布对比图，定量刻画了斑图中车辆的运动状态.由图可以发现，FCS模型中的速度分布不尽合理，静止状态(怠速)和畅行状态车辆的比例过高.如在密度ρ=0.12的情况下，FCS模型怠速状态所占的比例约为33%，而TLCA模型几乎不存在怠速状态运行的车辆.在TLCA模型中，非怠速和畅行状态的车辆比例均高于FCS模型中的同种状态.

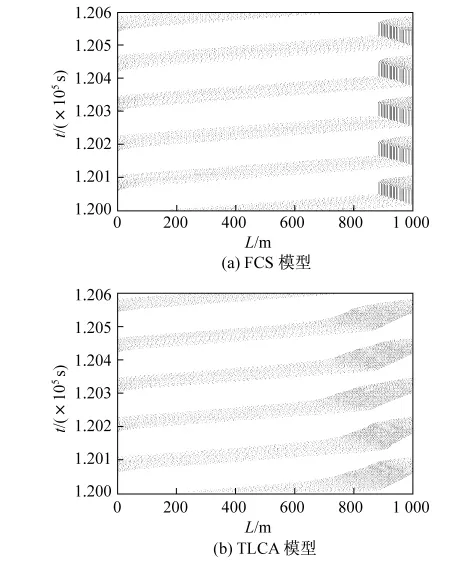
图5 在密度ρ=0.12的情况下，FCS模型和TLCA模型的时空演化斑图Fig.5 Spatio-temporal patterns for FCS and TLCA models at density ρ=0.12

图6 典型密度下，FCS模型和TLCA模型的速度分布对比Fig.6 Velocity distribution for FCS and TLCA models at typical densities

图7为两种模型在不同密度下车辆运动状态的统计结果.我们把车辆的运动分为4种状态：① 加速状态，v＞0，a＞0;② 减速状态，v＞0，a＜0;③匀速状态，v＞0，a=0;④怠速状态，v=0.由于加速状态时发动机加速运转，燃料的消耗和尾气的排放相对较大;减速过多影响车辆的运行效率和发动机工作效率;怠速状态时发动机空转，故这3种状态并不是我们所期望的.车辆只有在匀速状态下运行时，发动机才保持正常运转，所做的功都消耗在正常行驶上，因此，在此种状态下的行驶才是最为节约燃料和环保的.从图7中可以发现，随着密度的增加，怠速状态逐渐增多.相对于FCS模型，TLCA模型出现较少的怠速状态和较多的匀速和减速运动状态，且TLCA模型在系统达到临界密度ρc1之前几乎不存在怠速状态.值得指出的是，TLCA模型中减速状态偏多是由于车辆遇到红灯时缓慢减速造成的，这更加符合实际情况.总体而言，采用TLCA模型中的驾驶策略，可有效地减少机动车的尾气排放.

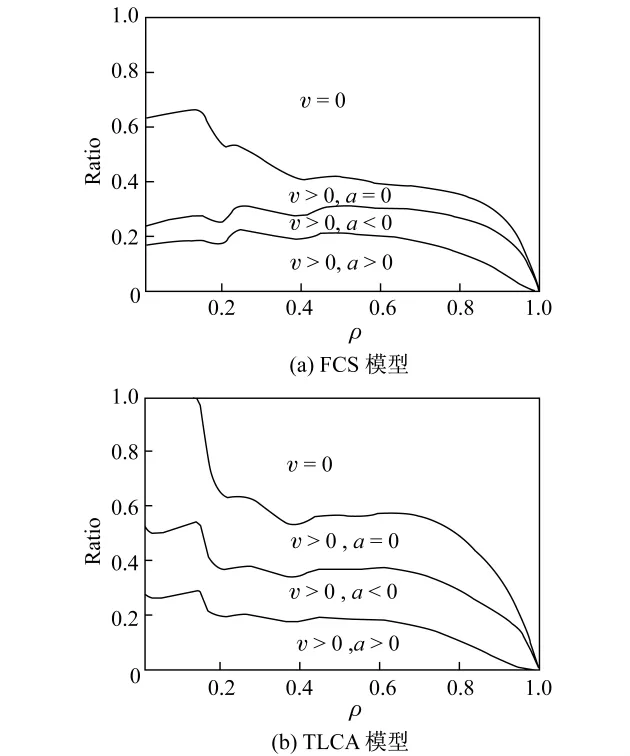
图7 FCS模型和TLCA模型的车辆不同运动状态分布Fig.7 Distribution of different moving states of vehicles in the FCS and TLCA models

3 结束语

本工作提出了一个描述交通灯控制下城市道路交通流演化的元胞自动机模型，即TLCA模型.在该模型中，交通灯对于路段上车辆的影响是全局的，即交通灯状态的改变会同时影响到路段上的所有车辆.而在FCS模型中，只是考虑了头车对交通灯的预判，并通过运动的变化向后传递交通灯的影响，与没有预判的FNS模型表现出了十分相似的运动特性.此外，TLCA模型还考虑了前车在下一时刻的预期运动.虽然TLCA模型给出的交通流宏观统计特征(基本图)与FCS模型没有显著的差别，但是在车辆运动的细观特征上具有显著的差异.与FCS模型相比，TLCA模型中车辆的运动更加平滑，这与实际交通现象符合.由于机动车频繁的加速和减速以及长时间处于怠速状态都会导致额外的尾气排放，采用本模型中的驾驶策略可使车辆匀速运动的状态明显增多，能较好地模拟现代生态驾驶理念下驾驶员的行为，即通过对交通前景的预判，明显减少怠速和速度骤减的状态，从而减少机动车的尾气排放，有效地缓解机动车尾气污染.该模型可以进一步推广到多车道城市交通流或考虑车辆在路口的转向，更好地刻画现实中复杂的交通现象.

［1］ PANISL I， BROEKX S， LIU R H. Modeling instantaneous traffic emission and the influence of traffic speed limits［J］.Science of the Total Environment，2006，371：270-285.

［2］ NAGELK，SCHRECKENBERGM.A cellular automaton model for freeway traffic［J］.J Phys I，1992，2：2221-2229.

［3］ BARLOVICR，SANTENL，SCHADSCHNEIDERA，et al.Metastable states in cellular automata for traffic flow［J］.Eur Phys J B，1998，5：793-800.

［4］ KNOSPEW，SANTENL，SCHADSCHNEIDERA，et al.Towards a realistic microscopic description of highway traffic［J］.J Phys A，2000，33：477-485.

［5］ BIHAM O，MIDDLETON A，LEVINED A.Selforganization and a dynamical transition in traffic flow models［J］.Phys Rev A，1992，46：6124-6127.

［6］ CHOWDURYD，SCHADSCHNIDERA.Self-organization of traffic jams in cities：effects of stochastic dynamics and signal periods［J］.Phys Rev E，1999，59：1311-1314.

［7］ BROKFELDE，BARLOVICR，SCHADSCHNEIDERA，et al.Optimizing traffic lights in a cellular automaton model for city traffic［J］.Phys Rev E，2001，64：056132.

［8］ SASAKIM，NAGATANIT.Transition and saturation of traffic flow controlled by traffic lights［J］.Physica A，2003，325：531-546.

［9］ HEH D，DONGL Y，DAIS Q.Simulation of traffic flow with trafficlightstrategiesvia a modified cellular automaton model［J］.Journal of Shanghai University：English Edition，2006，10(3)：189-191.

［10］ JIANGR，WU Q S.A stoppedtimedependent randomization cellular automata model for traffic flow controlled by traffic light［J］.Physica A，2006，364：493-496.

［11］ 刘慕仁，薛郁，孔令江.城市道路交通问题与交通流模拟［J］.力学与实践，2005，27(1)：1-6.