具有一般非线性接触率及潜伏年龄结构的SEIS传染病模型稳定性分析

锁要红， 张仲华

(1.西安科技大学理学院，西安710054;2.西安交通大学航天航空学院，西安710049; 3.陕西师范大学数学与信息科学学院，西安710062)

近几十年来，传染病动力学的研究进展迅速，并且大量的数学模型被用于分析各种各样的传染病问题［1-2］.一般的传染病模型总是假设所有的染病者在整个患病期内具有相同的传染率，显然这个假设在研究流感或性传播疾病(如淋病)等传染病时是合理的.但对于染病期较长的传染病，变化的传染率才能更准确地刻画传染病的传播规律及预测传染病在人群中的传播趋势.

近年来，染病年龄结构数学模型正越来越多地被关注.Thieme等［3］假设传染率及潜伏期依赖于染病年龄和饱和接触率，建立了一类HIV病毒在同性人群中传播的SIA模型.Kim等［4］建立了一类具有隔离和变化传染率的SIR模型，讨论了非负解的存在性及唯一性.Kim［5］讨论了平衡点的存在性及渐近稳定性.Kribs-Zaleta等［6］建立了一类具有急性和慢性传染阶段、变化传染率及变化恢复率的染病年龄结构模型，研究了平衡点的稳定性，并得到了后向分歧的存在条件.Inaba等［7］建立了一类查更斯疾病传播规律的染病年龄结构模型，证明了平衡点的稳定性.李佳等［8］建立了一类在宿主中病原体能够变异产生一个二次感染病毒株的染病年龄结构模型，讨论了平衡点的稳定性，并得到了Hopf分歧的存在条件.徐文雄等［9］考虑宣传教育对疾病控制的意义，建立了一类具有双线性传染率的染病年龄结构模型.张仲华等［10］研究了具有一般非线性接触率SIRS传染病模型全局非负解的存在唯一性以及平衡点的渐近稳定性.从生物意义上讲，感染者在染病期内的传染力依赖于其染病年龄，这将更符合一些染病期较长的传染病的情况.从数学意义上看，这类模型不同于以往的单纯的常微分方程模型，而是由常微分方程和偏微分方程组成的模型，这类模型的研究方法也有别于常微分方程模型.

由医学卫生知识可知，一些疾病如艾滋病等具有较长的潜伏期(指从病原体侵入人体起到出现临床症状的时间段)，且在潜伏期内，疾病的传播起重要作用.又由于社会经济的高度发展及国际间的往来日趋频繁，很难用一个具有很好性质的函数去刻画人与人之间相互接触的复杂关系.基于此，本研究在文献［10-11］的基础上，考虑具有一般非线性接触率及潜伏年龄结构的SEIS传染病模型的平衡点的存在性及渐近稳定性，得到一个地方病平衡点指数稳定的一般性条件.

1 模型的建立

张仲华等［11］将研究对象分成易感者、潜伏者及染病者类，考虑常数输入和因病死亡等因素，并假设疾病仅在感染期内传染，建立了具有 Michaelis-Menten接触率的SEIS模型，即

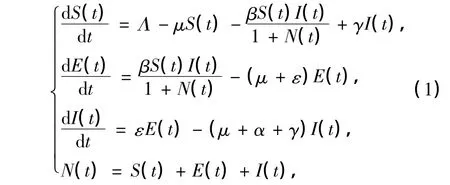
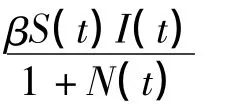
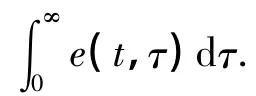
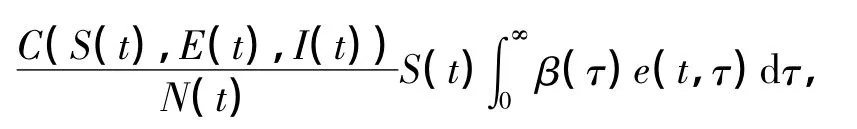
式中，N(t)=S(t)+E(t)+I(t)为t时刻的种群规模.综上，模型(1)可转化为如下具有潜伏年龄结构的SEIS传染病模型：

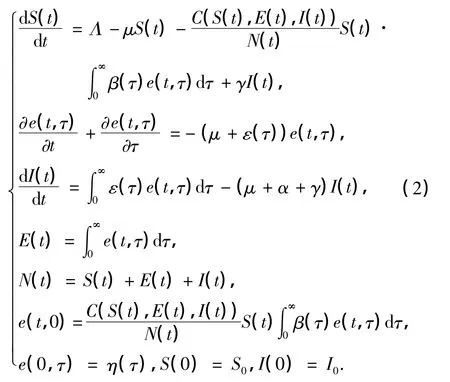
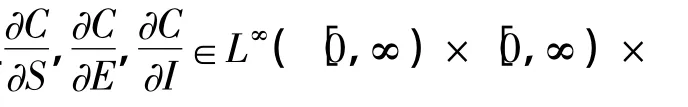
2 平衡点的存在性及无病平衡点的稳定性

为方便起见，记

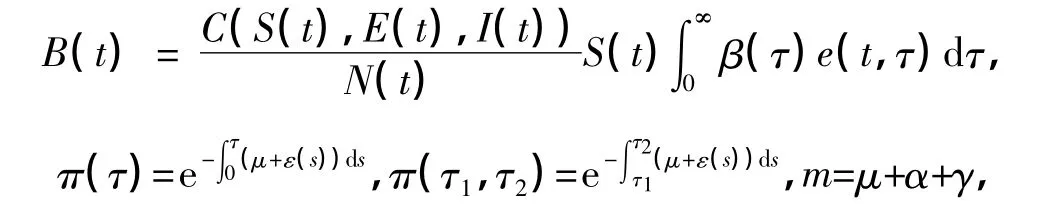
式中，B(t)的生物意义为t时刻各个年龄阶段的潜伏者新感染的人数.设(S，e(·)，I)为系统(2)的稳态解，则稳态解存在的充分必要条件是其满足下述方程组：

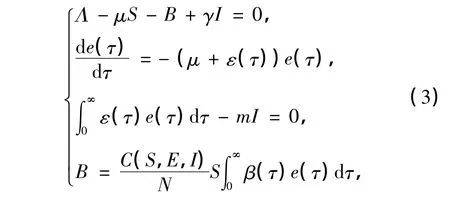
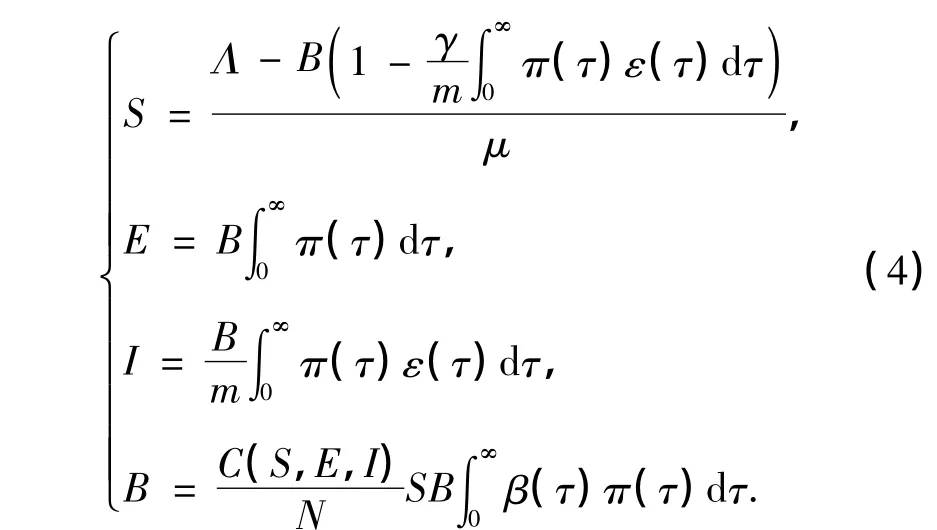
由式(4)可知，S，E，I为B的连续函数.定义

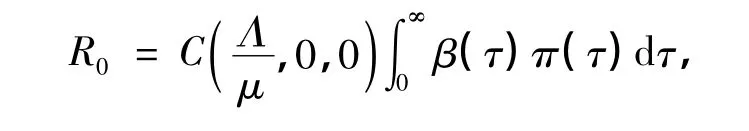
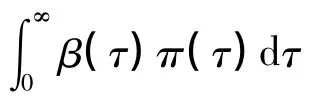
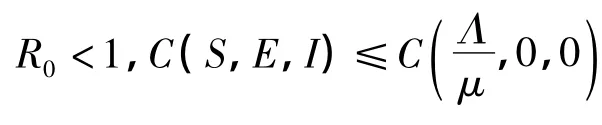
3 地方病平衡点的指数稳定性

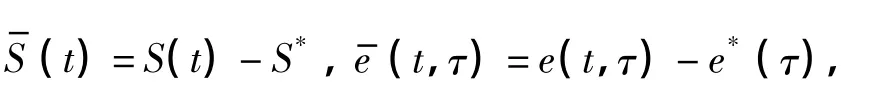
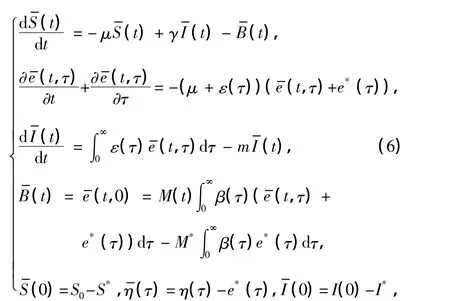
将式(6)中的第二个方程沿特征线t=τ积分，得

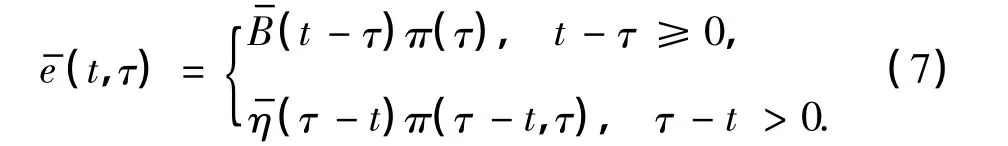
将式(7)代入(6)，且将所得方程从0到t积分，得

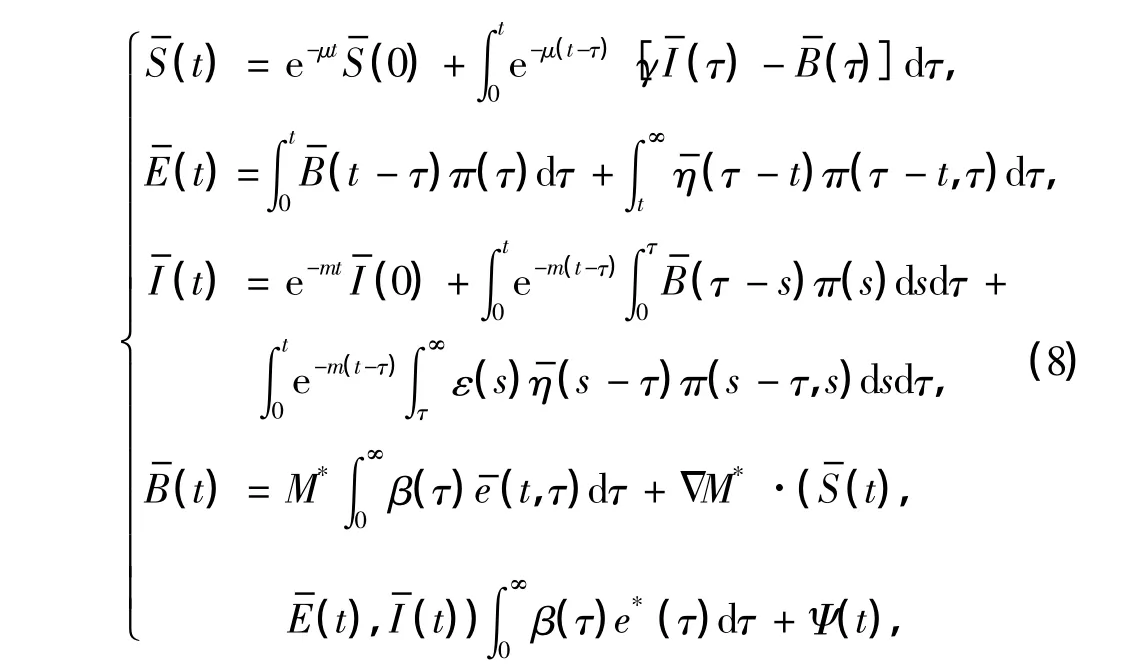
式中，

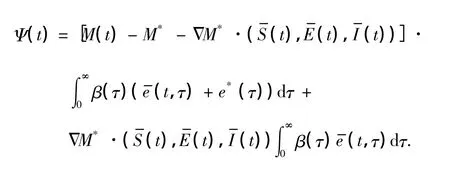
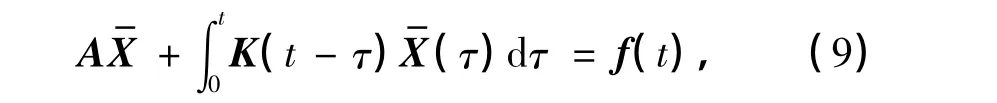
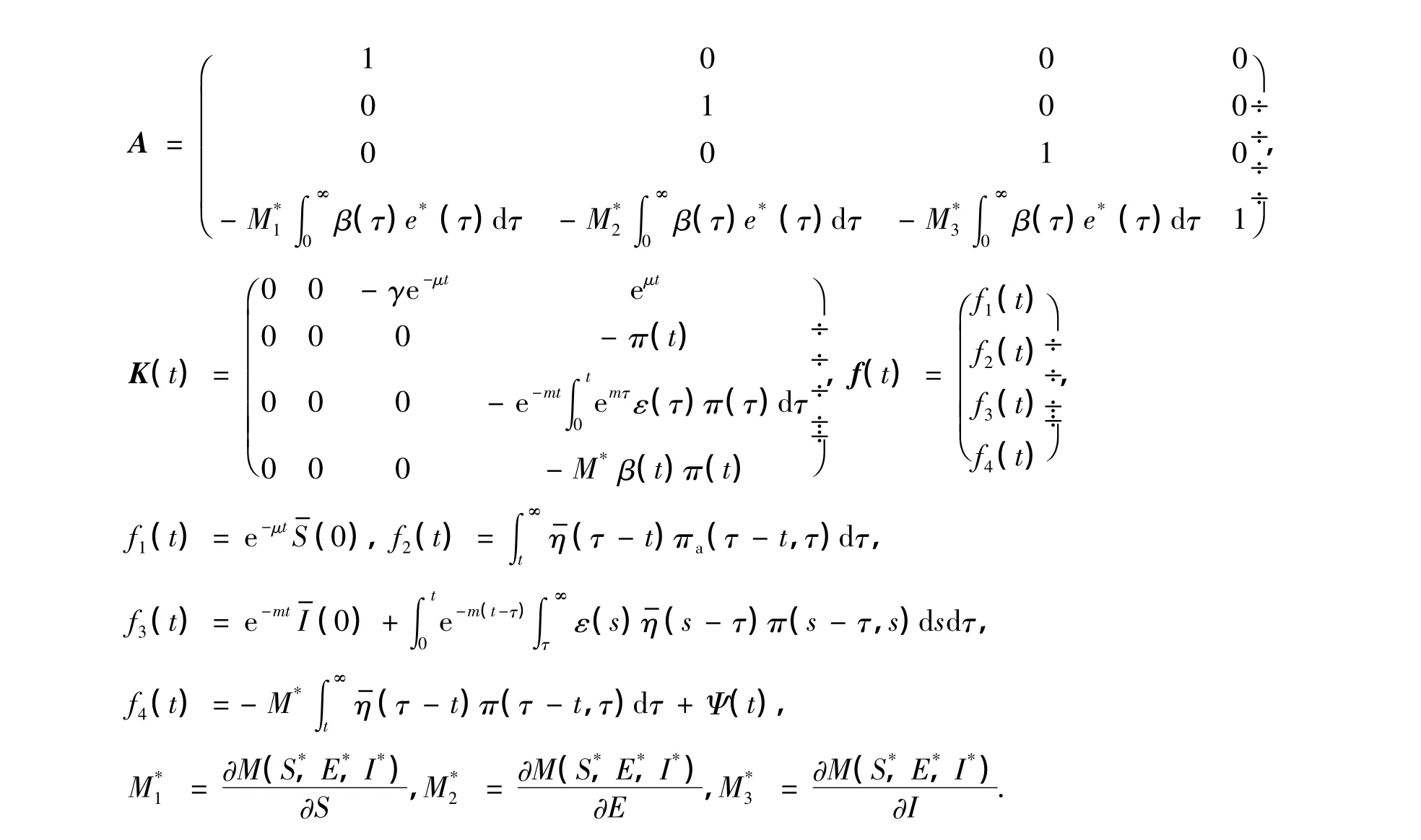
式中，不难证明，存在正常数D，使得

‖K(t)‖，‖K'(t)‖，‖K″(t)‖≤De-μt. (10)

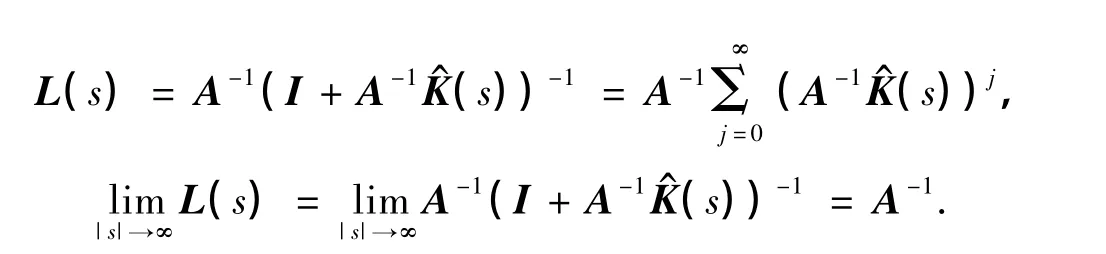
为讨论地方病平衡点的渐近稳定性，与文献［5，10］类似，作如下假设：

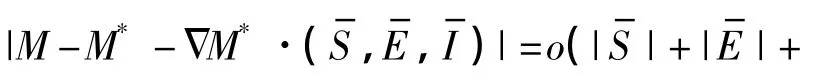
定理2 在假设P1下，如果det(A+(s))的所有根都具有负实部，则存在正常数a，b，δ，使得当初值S0，η(τ)，I0满足|S0|+|I0|+‖η(τ)‖1＜δ时，系统(2)的解具有下述性质：

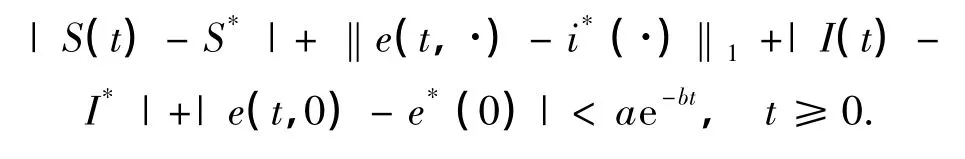
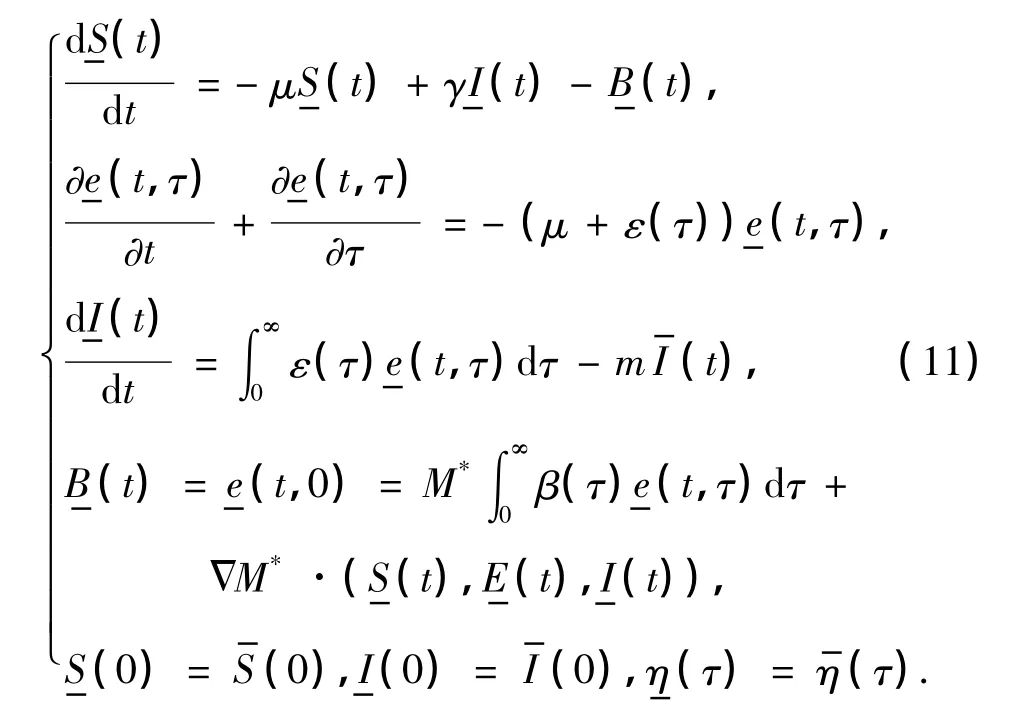
显然有

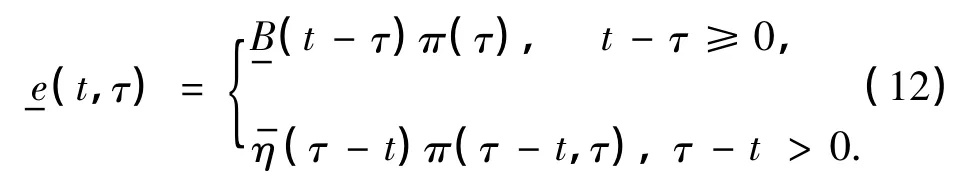
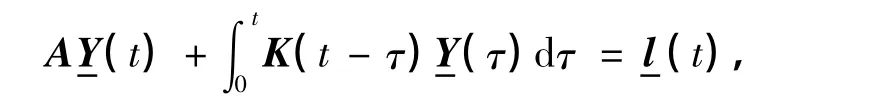
其中

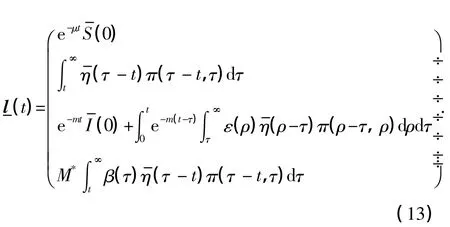
类似于前面的讨论，可得

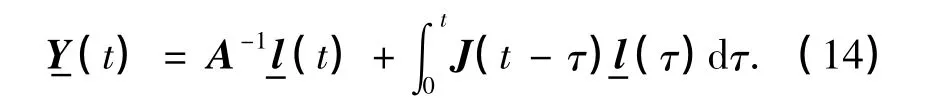
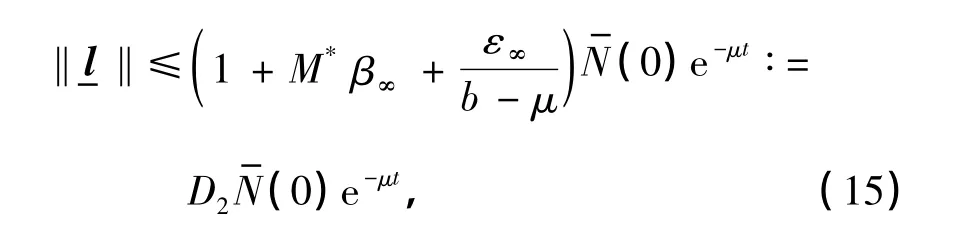
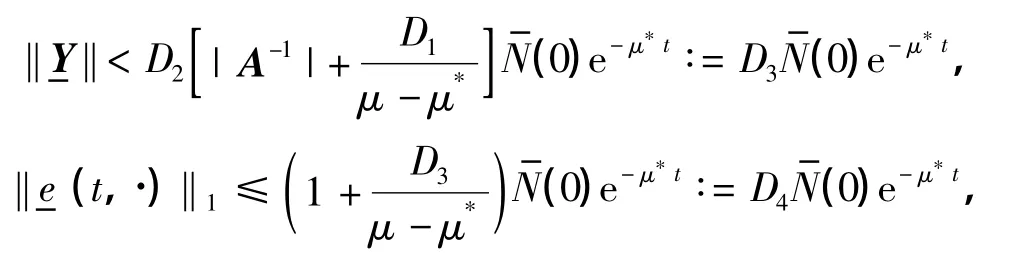
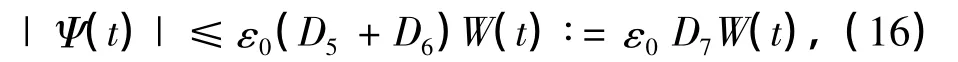
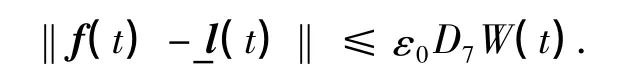
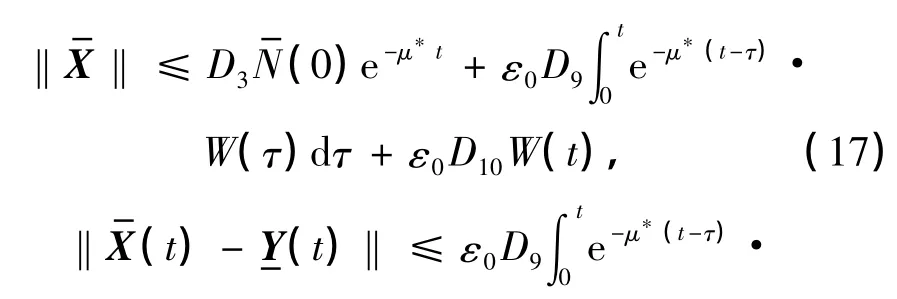
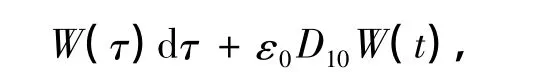
式中，D9=D1D7，D10=|A-1|D7.显然有

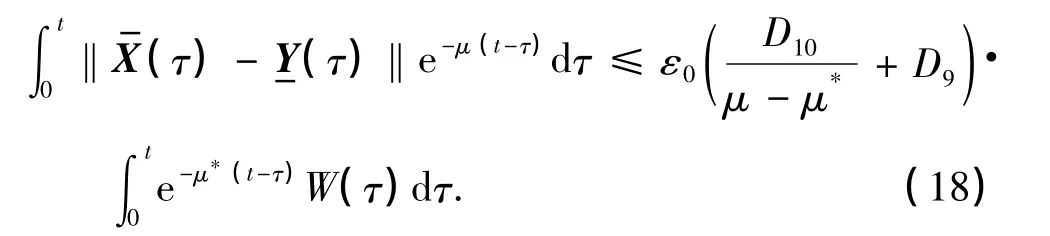
由式(7)，(12)和(18)，可得

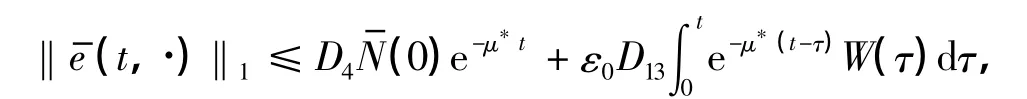
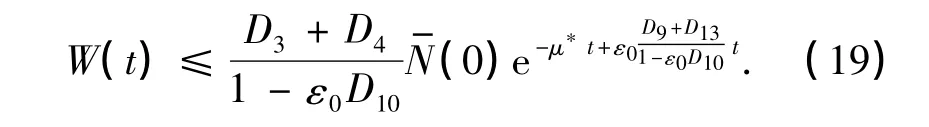
4 结束语

本研究基于文献［11-12］，建立了一类具有一般非线性接触率及潜伏年龄结构的SEIS传染病模型，讨论了地方病平衡点的存在性、无病平衡点的全局渐近稳定性及地方病平衡点的指数稳定性，得到了地方病平衡点指数稳定的一般性条件.

［1］ 陆征一，周义仓.数学生物学进展［M］.北京：科学出版社，2006：30-93.

［2］ 马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究［M］.北京：科学出版社，2004：27-69.

［3］ THIEMEH R，CASTILLO-CHAVEZC.How may infectionage-dependent infectivity affect the dynamics of HIV/ AIDS?［J］.SIAM J Appl Math，1993，53(5)：1447-1479.

［4］ KIMM Y，MILNERF A.A mathematical model of epidemics with screening and variable infectivity［J］.Math Comput Modelling，1995，21(7)：29-42.

［5］ KIMM Y.Existence of steady state solutions to an epidemic model with screening and their asymptotic stability［J］.Appl Math Comput，1996，74(1)：37-58.

［6］ KRIBS-ZALETACM，MARTCHEVAM.Vaccination strategies and backward bifurcation in an age-sinceinfection structured model［J］.Math Biosci，2002，177/178(2)：317-332.

［7］ INABAH，SEKINEH.A mathematical model for Chagas disease with infection-age-dependent infectivity［J］.Math Biosci，2004，190(4)：39-69.

［8］ LIJ，ZHOUY C，MAZ Z，et al.Epidemiological models for mutating pathogens［J］.SIAM J Appl Math，2004，65(1)：1-23.

［9］ 徐文雄，张仲华.年龄结构SIR流行病传播数学模型渐近分析［J］.西安交通大学学报，2003，37(10)：1086-1089.

［10］ ZHANGZ H，PENGJ G.A SIRS epidemic model with infection-age dependence［J］.J Math Anal Appl，2007，331(2)：1396-1414.

［11］ 张仲华，徐文雄.一类SEIS流行病传播数学模型的渐近分析［J］.陕西师范大学学报，2004，32(3)：1-3.

［12］ 王拉娣，李健全.一类带有非线性传染率的SEIS传染病模型的定性分析［J］.应用数学和力学，2006，27 (5)：193-695.