关于一个非齐次核的Hilbert型积分不等式

杨必成

(广东教育学院数学系，广州510303)

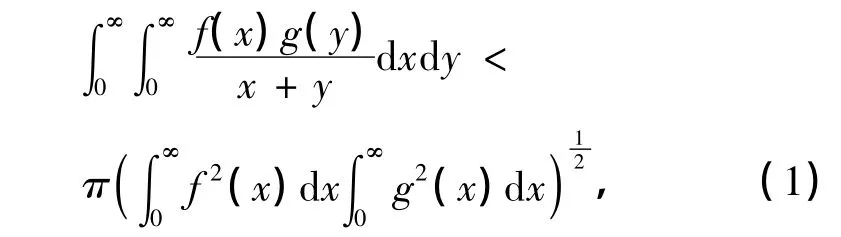
式中，常数因子π为最佳值.式(1)为分析学中的重要不等式，它的推广应用可参见文献［2-3］.注意到式(1)的核是-1齐次的，文献［4］系统综述了负数齐次核的参量化Hilbert型不等式的研究方法与研究成果.近年来，相关研究开始由齐次核转向非齐次核的不等式［5-9］，如文献［6］中得到的具有最佳常数因子的积分不等式，即

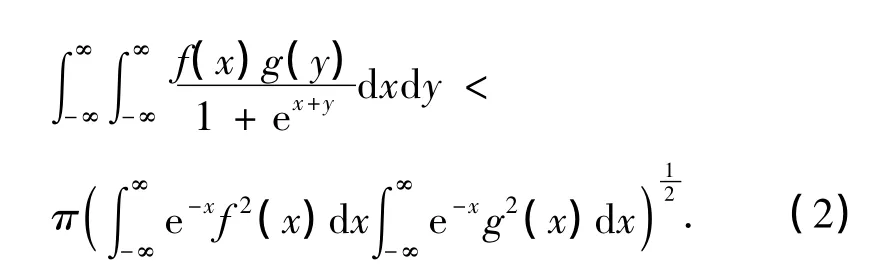
本研究应用权函数的方法，建立如下类似于式(2)的非齐次核的Hilbert型积分不等式：

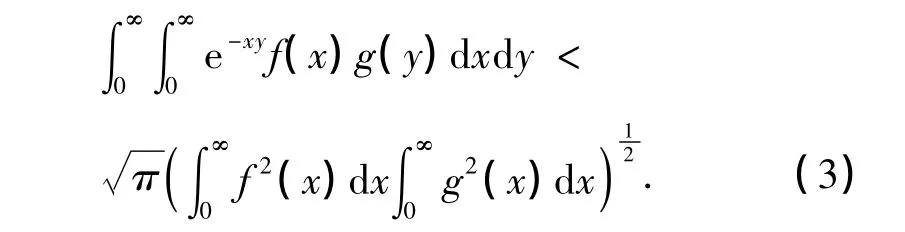
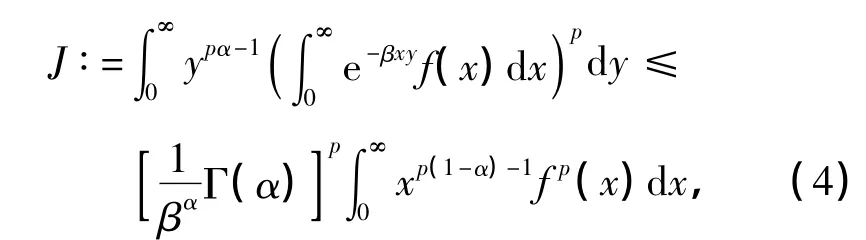
证明 配方，并由Hölder不等式［11］，得

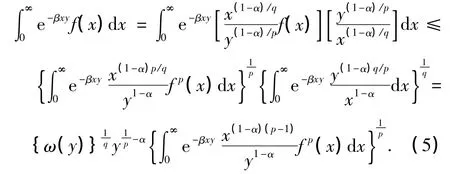
这里，定义如下权函数：

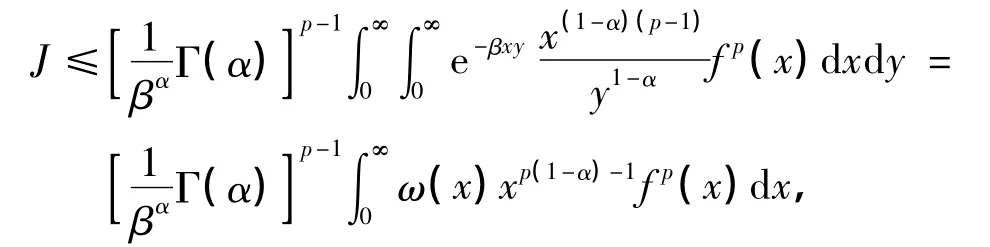
再代入ω(x)的值，式(4)得证.

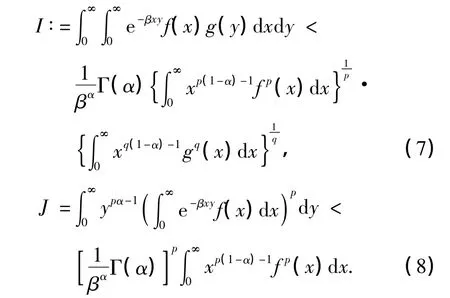
证明 若有y＞0，使式(5)等号成立，则有不全为0的常数A，B，使

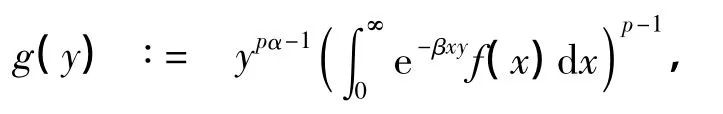
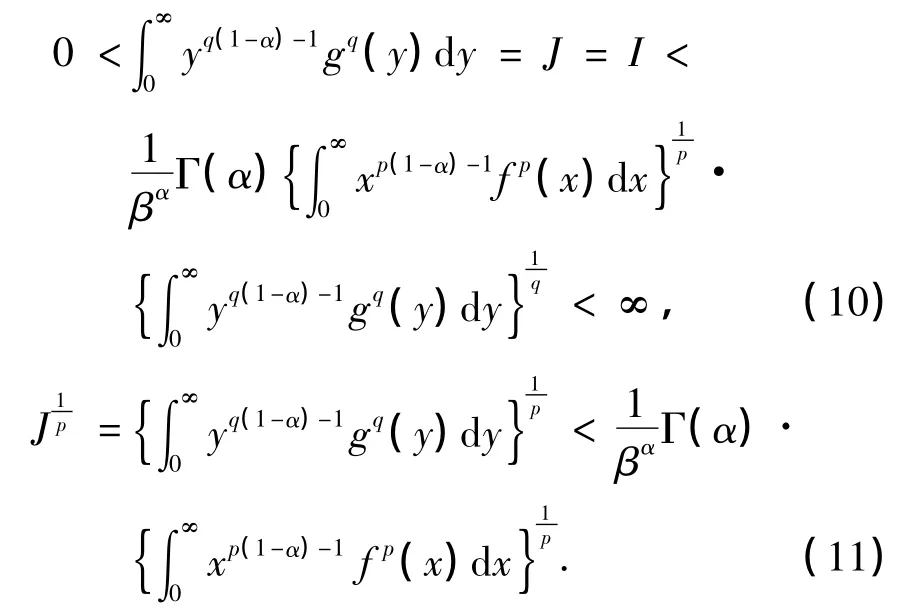
对式(11)两边取p次方，可证得式(8)成立，且式(8)与式(7)等价.证毕.

证明 任0＜ε＜qα，设

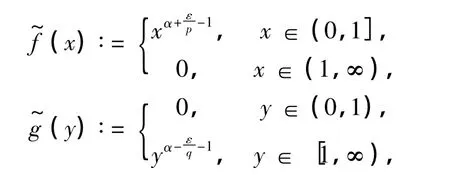
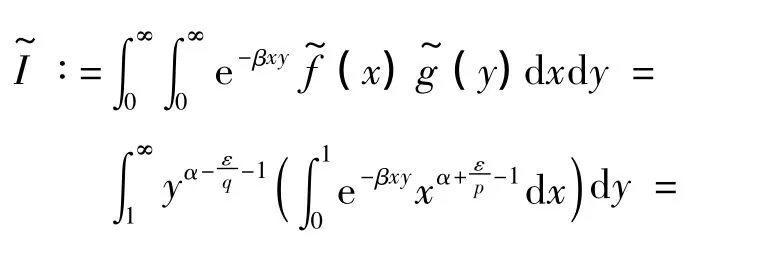
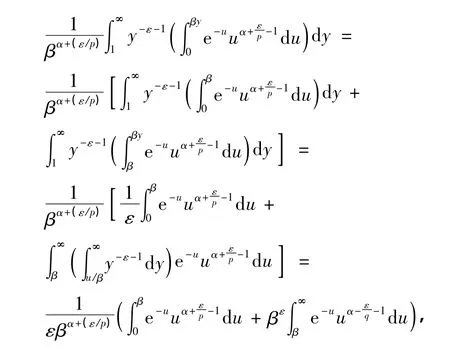
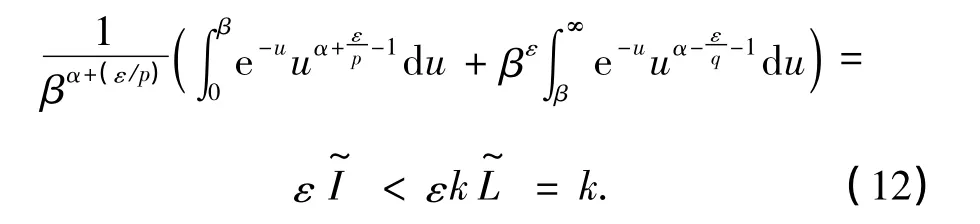
由Fatou引理［12］，易得

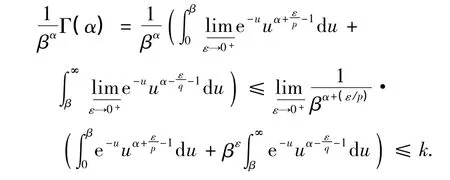
定理3 若0＜p＜1，其他条件同定理1所述，则式(7)与(8)的逆向等价式成立，且相应的常数因子仍为最佳值.

证明 证法与定理1、定理2类似，先由逆向的Hölder不等式［11］，可得式(4)及(9)的逆式成立.由此易得式(8)的逆式成立，再将其代入式(9)的逆式，可得式(7)的逆式成立.反之，设有式(7)的逆式成立，置与定理1同样的g(y)，则由式(4)的逆式知，J＞0.若J=∞，则式(8)的逆式显然成立;若J＜∞，则由式(7)的逆式，易得式(10)及(11)的逆式成立，故有式(8)的逆式成立，且其与式(7)的逆式等价.

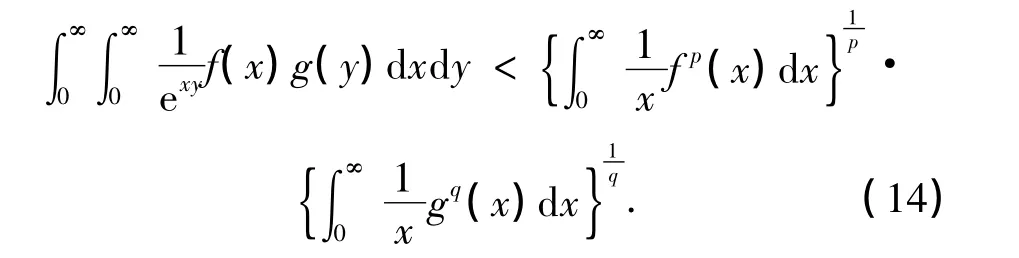
［1］ HARDYG H，LITTLEWOODJ E，POLYAG.Inequalities［M］.Cambridge：Cambridge University Press，1952.

［2］ MITRINOVICD S，PECARICJ E，FINKA M.Inequalities involving functions and their integrals and derivatives［M］.Boston：Kluwer Academic Publishers，1991.

［3］ 杨必成.算子范数与Hilbert型不等式［M］.北京：科学出版社，2009.

［4］ 杨必成.参量化的Hilbert型不等式研究综述［J］.数学进展，2009，38(3)：257-268.

［5］ YANGB C.On the norm of an integral operator and applications［J］.J Math Anal Appl，2006，321：182-192.

［6］ YANGB C.A new Hilbert-type inequality［J］.Bull Belg Math Soc，2006，13：479-487.

［7］ XU J S. Hardy-Hilbert’s inequalities with two parameters［J］.Advanced in Mathematics，2007，36 (2)：63-76.

［8］ YANGB C.On the norm of a Hilbert’s type linear operator and applications［J］.J Math Anal Appl，2007，325：529-541.

［9］ 刘琼.一个多参数的Hilbert型积分不等式［J］.吉林大学学报：理学版，2009，47(5)：903-908.

［10］ 王竹溪，郭敦仁.特殊函数论［M］.北京：科学出版社，1979.

［11］ 匡继昌.常用不等式［M］.济南：山东科技出版社，2004.

［12］ 匡继昌.实分析引论［M］.长沙：湖南教育出版社，1996.