Timoshenko模型桩水平振动的动力刚度

姚 戈，杨 骁

(上海大学土木工程系，上海200072)

作为工程结构的一种重要基础形式，桩基础应用已有数百年的历史［1］.然而，由于土介质的复杂力学性能以及桩基应用领域的不断扩大，桩-土相互作用，尤其是动力相互作用的研究至今仍是土木工程等相关研究领域的重要课题.

在桩-土相互作用的连续介质模型中，将土介质视为连续体，在一定的简化假定下，可较精确地揭示桩-土间的相互作用机理.基于弹性理论，将桩等效为Euler-Bernoulli梁，Novak等［2-3］首先建立了桩-土相互作用的二维和三维连续介质模型，研究并实验验证了弹性土中桩水平振动的动力特性.李耀庄等［4］基于二维模型，分析了单桩的水平振动及水平-摇摆耦合振动，考察了各种因素对单桩动力刚度的影响.这些模型及相关的解析解对揭示桩-土相互作用机理起到了积极的作用.为考虑桩-土相互作用的非线性效应，Nogami等［5］提出了一种边界层模型，而Nogami等［6］和El Nagger等［7］提出了一个考虑土非线性效应的简单连续介质模型.Chau等［8］对端承桩周围内部土介质应用双曲本构模型，通过内外土介质区域的精确连续性条件，分析了端承桩的非线性水平振动问题.Das等［9］和刘鑫等［10］将悬浮桩截面下土层等效为和桩紧密连接的“土桩”，研究了悬浮桩水平振动的动力特性.Hamid等［11］考虑了桩附近土的非线性行为，提出了一种非线性有限元-边界元耦合方法.近年来，众多学者关注饱和土中桩基的力学行为，Nogami等［12］以饱和土的Biot模型为基础，研究了超孔隙水压力对桩力学特性的影响.利用虚拟桩的概念和积分方程，Zeng等［13］首先在频率域中研究了饱和弹性土中垂直受载单桩的动力特性.Lu等［14］在频域内研究了饱和半空间中悬浮桩在P，SV波作用下的动力响应.而余俊等［15］给出了简谐稳态水平振动下桩动力响应的解析解，讨论了可退化为干土中桩响应的条件.Han［16］提出了分析桩-土动力相互作用的实用算法，并与有限元方法进行了比较.

目前，在桩-土相互作用的理论分析中，众多学者将桩视为Euler-Bernoulli梁.然而，众所周知，由于Euler-Bernoulli梁忽略了梁横截面的剪切变形效应，因此，该模型所得的若干结果，如桩头刚度等，均为实际值的上限.例如，对于细长桩，基于 Euler-Bernoulli梁模型的分析计算基本满足了工程要求，而对于大直径桩，计算结果误差较大，必须予以修正.Timoshenko梁模型可考虑梁横截面的剪切变形效应［17］，因此，将桩视为Timoshenko梁研究桩-土相互作用具有一定的学术价值和应用背景.

本研究在Nogami等［18］关于桩水平振动土阻抗研究的基础上，将桩等效为 Timoshenko梁，得出Timoshenko模型端承桩水平振动的动力学特性.通过将Timoshenko梁挠度和转角的耦合控制方程进行解耦，可求得Timoshenko梁在土层阻抗作用下的解析通解.在此基础上，利用桩-土相互作用时桩-土界面的位移协调条件，得到确定待定系数的线性方程，从而求得问题的封闭解.最后，给出桩头动力刚度随频率的变化曲线，研究了物性和几何参数对刚度的影响，并与Euler-Bernoulli模型桩的结果进行了比较.

1 桩水平振动下的土阻抗

设厚为H的各向同性黏弹性土层中有一半径为R0的黏弹性圆柱桩(见图1)，其中桩的弹性模量和剪切模量分别为Ep和Gp，泊松比为νp，材料阻尼系数为ξp，体密度为ρp，线质量密度mp=πR20ρp，横截面惯性矩为Ip;土介质的剪切模量为G，材料阻尼系数为ξ，泊松比为ν，体密度为ρ.假定在桩-土的耦合振动中，桩和土层发生小变形且桩-土之间紧密连接，不产生任何相对位移.

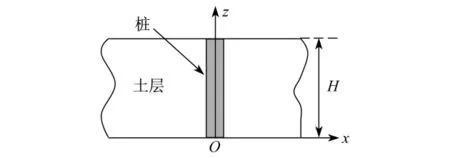
图1 土层中的端承桩Fig.1 End-bearing pile in a soil layer

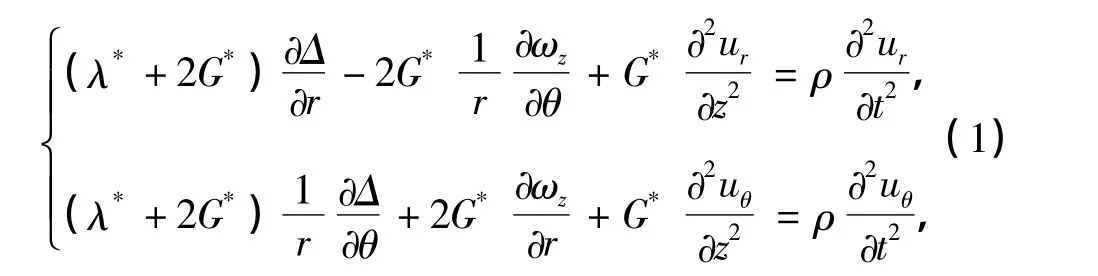
忽略土体的竖向位移，土体在柱坐标系Orθz下的动力控制方程［8］为

式中，λ*=2νG*/(1-2ν)和G*=G(1+2ξi)为土体的复Lamé常数，i=，ur和uθ分别为土层的径向和环向的位移分量，并且

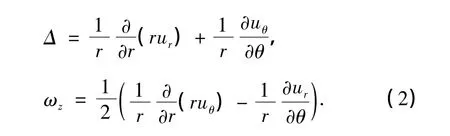
将式(3)代入运动方程(1)，可得势函数Φ和Ψ的控制方程.若桩在Oxz平面内运动，则挠度可表示为

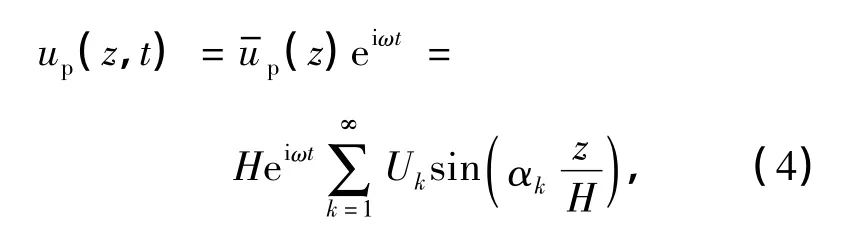
而相应的土阻抗［8］可表示为

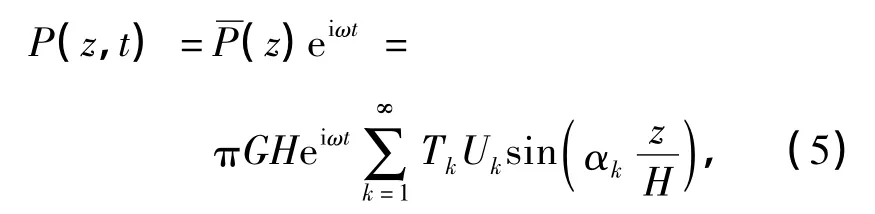
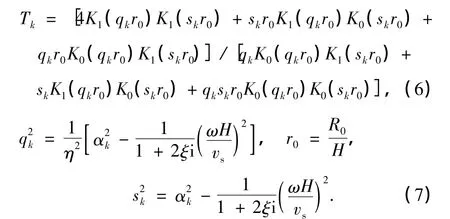
2 桩-土系统的耦合振动

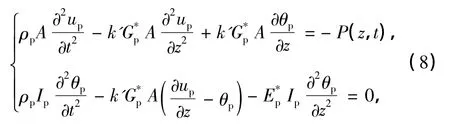
将桩视为Timoshenko梁，若桩在Oxz平面内变形，则桩挠度up(z，t)和横截面转角θp(z，t)的控制方程如下：

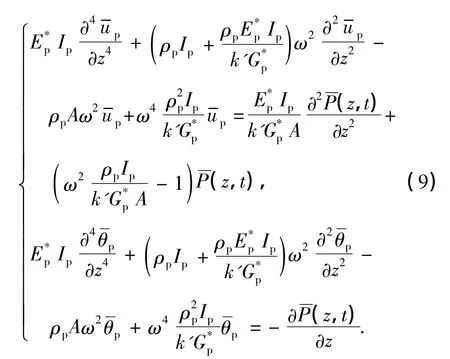
由方程(9)中的第一个方程，可得

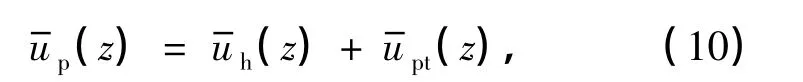
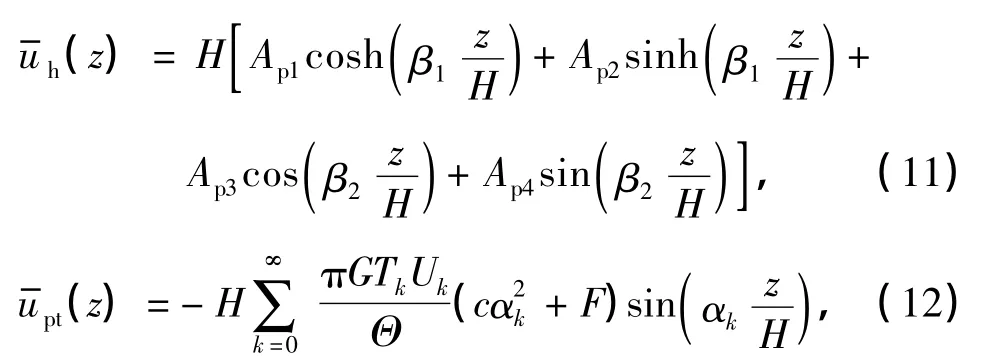
式中，Ap1，Ap2，Ap3，Ap4为待定常数.

利用式(4)和(10)，可得

于是，有

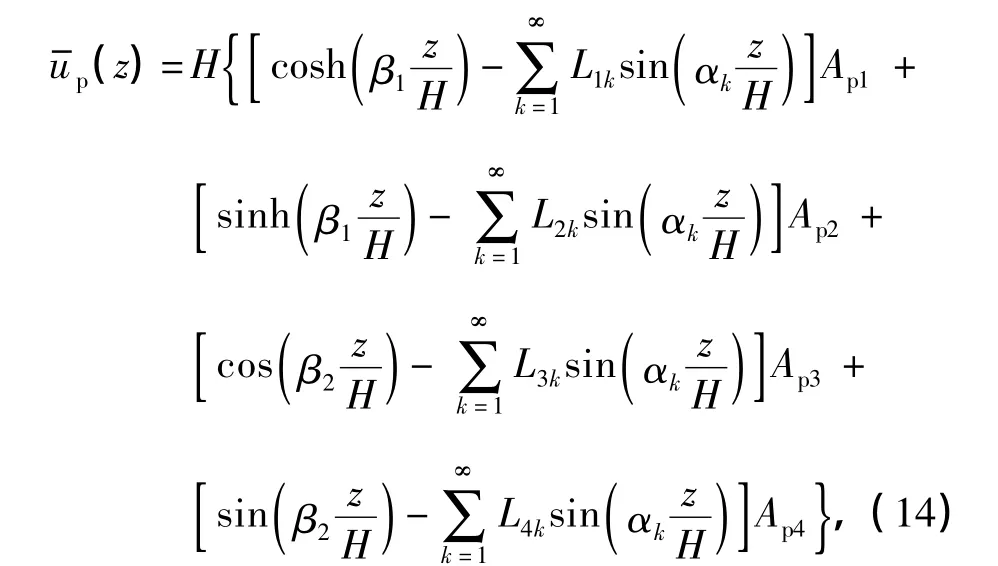
式中，

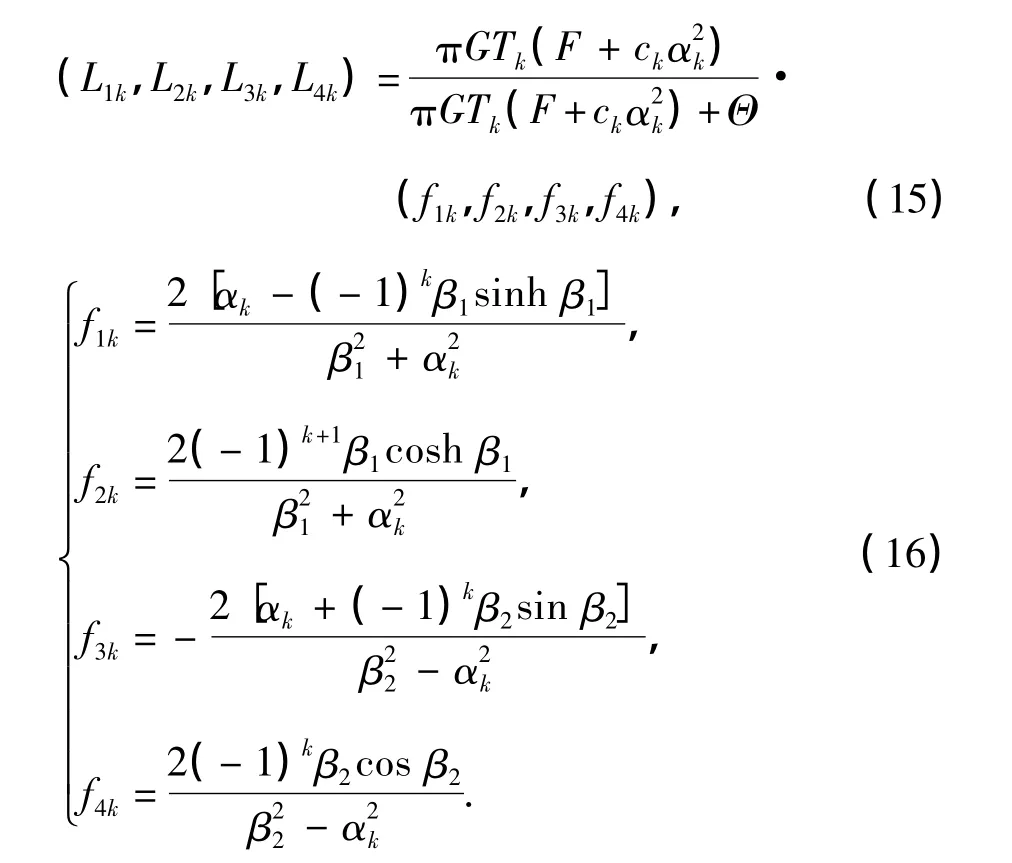
同理，由方程(9)中的第二个方程，可得

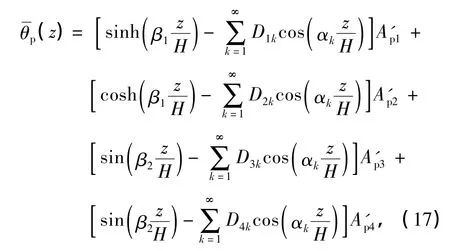
由方程(8)中的第一个方程，可得

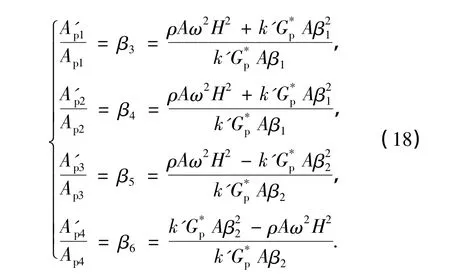
由桩底约束条件、桩头边界条件以及关系式(18)，可确定待定常数Ap1，Ap2，Ap3，Ap4，A'p1，A'p2，A'p3和A'p4.因此，可得桩弯矩Mp(z)和剪力Qp(z)分别为

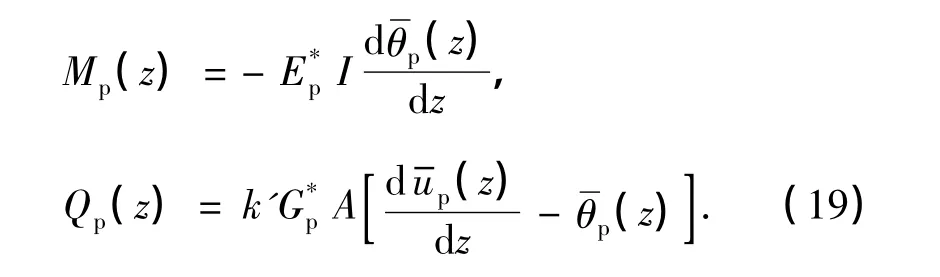
3 动力刚度及数值结果

将在桩头z=H处产生单位水平位移、且转角为0所需的剪力和弯矩分别定义为桩头复刚度KQu和KMu;而将在桩头z=H处产生单位转角、且水平位移为0的剪力和弯矩分别定义为桩头复刚度KQθ和KMθ，其中复刚度的实部为桩的真实刚度，虚部表示由于弹性波传播和材料内部耗能而引起的阻尼特性.

对于桩底部(z=0)的约束条件，如果底端为铰支和固支，则边界条件分别为

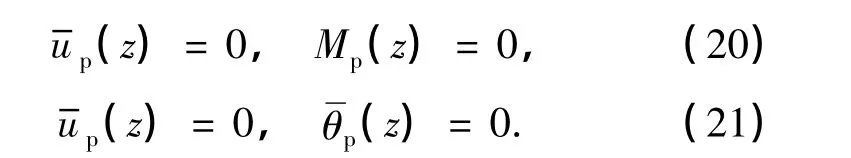
而桩头(z=H)的边界条件为

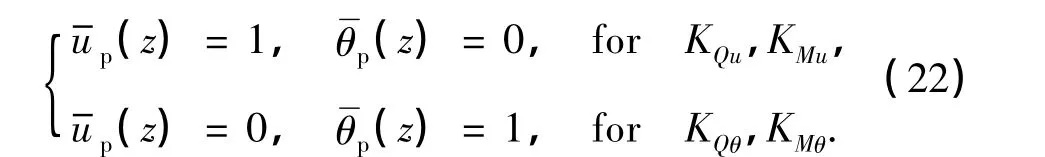
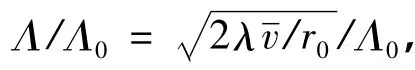
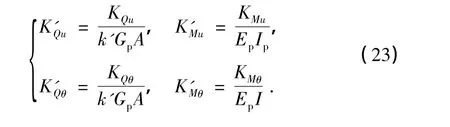
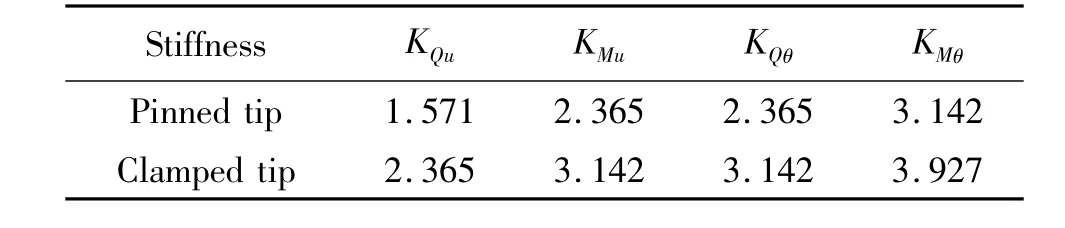
表1 不同刚度和约束条件的Λ0Table 1 Value Λ0for different stiffnesses and constraints

4 结束语

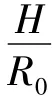
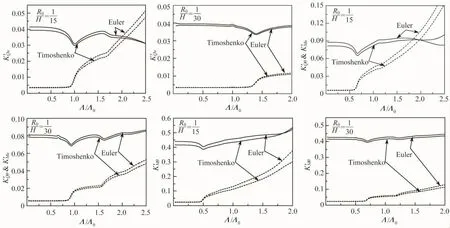
图2 不同桩径比下2种模型计算结果的比较Fig.2 Results comparisons between two models for different slenderness ratio of pile

图3 =时的桩头刚度Fig.3 Pile-head stiffnesses when=

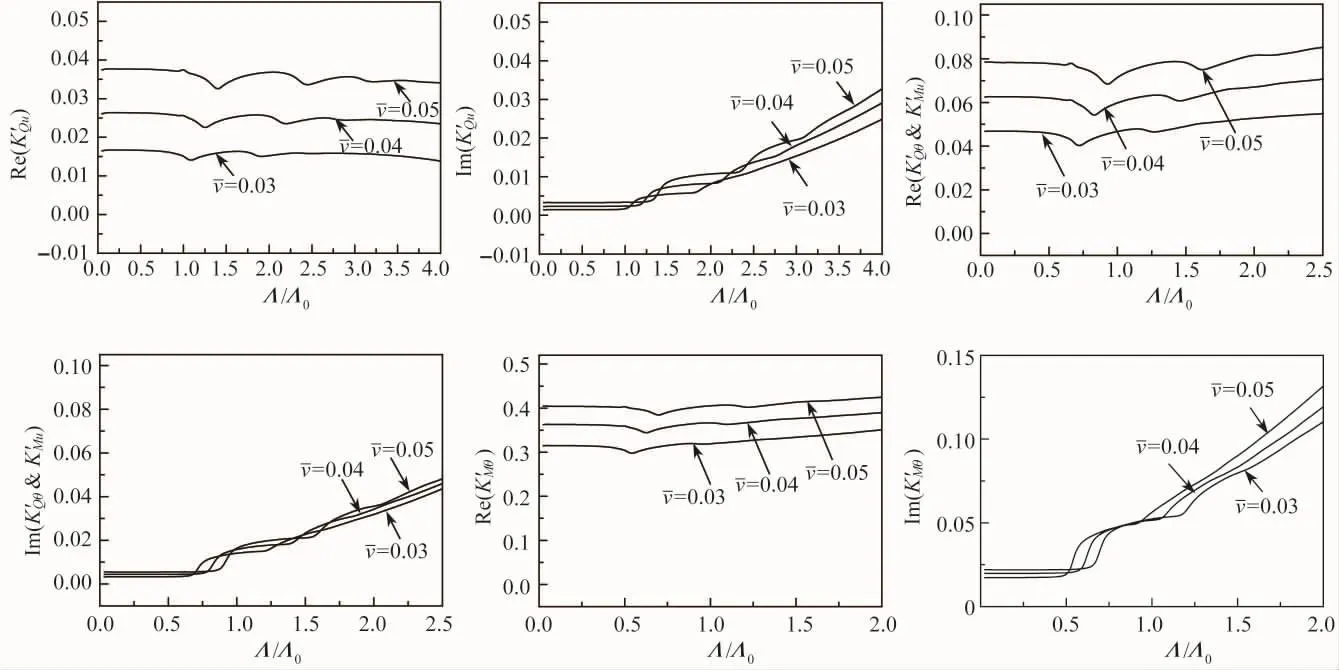
图4 =时的桩头刚度Fig.4 Pile-head stiffnesses when=

［1］ NOVAKM.Piles under dynamic loads［C］∥Proceedings of the 2nd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics.1991：2433-2457.

［2］ NOVAKM.Dynamic stiffness and damping of piles［J］.Canadian Geotechnical Journal，1974，11(4)：574-598.

［3］ NOVAKM，NOGAMIT.Soil-pile interaction in horizontal vibration［J］.Earthquake Engineering and Structure Dynamics，1977，5(3)：263-281.

［4］ 李耀庄，李博.单桩水平及水平-摇摆耦合振动分析［J］.世界地震工程，2006，22(4)：160-165.

［5］ NOGAMIT，NOVAKM.Coefficients of soil reaction to pile vibration［J］.Journal of Geotechnical Engineering Division，1980，106(5)：565-570.

［6］ NOGAMIT，OTANIJ，KONAGAIK，et al.Nonlinear soil-pile interaction model for dynamic lateral motion［J］.Journal of Geotechnical Engineering，1992，118 (1)：89-106.

［7］ ELNAGGERM H，NOVAKM.Nonlinear analysis for dynamic lateral pile response［J］.Soil Dynamics and Earthquake Engineering，1996，15(4)：233-244.

［8］ CHAUK T，YANGX.Nonlinear interaction of soil-pile in horizontal vibration［J］.Journal of Engineering Mechanics，2005，131(8)：847-858.

［9］ DASY C，SARGANDS M.Forced vibrations of laterally loaded piles［J］. InternationalJournalofSolid Structure，1999，36(33)：4975-4989.

［10］ 刘鑫，杨骁.悬浮桩水平振动的动力刚度［J］.岩土力学，2008，29(4)：1021-1026.

［11］ MASOUMIH R，FRANCOISS，DEGRANDEG.A nonlinear coupled finite element-boundary element model for the prediction of vibrations due to vibratory and impact pile driving［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2009，33(2)：245-274.

［12］ NOGAMIT，RENF，CHENJ，et al.Vertical vibration of pile in vibration-induced excess pore pressure field［J］.Journal of Geotechnical and Geoenvironmental Engineering，1997，123(5)：422-429.

［13］ ZENGX，RAJAPAKSER K N D.Dynamic axial load transfer from elastic bar to poroelastic medium［J］.Journal of Engineering Mechanics，1999，125(9)：1048-1055.

［14］ LUJ F，JENGD S.Poroelastic model for pile-soil interaction in a half-space porous medium due to seismic waves［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2008，32(1)：1-41.

［15］ 余俊，尚守平，李忠，等.饱和土中端承桩水平振动动力响应分析［J］.岩土工程学报，2009，31(3)：408-415.

［16］ HANY C.Study of vibrating foundations considering oilpile-structure interaction for practical applications［J］.Earthquake Engineering and Engineering Vibration，2008，7(3)：321-327.

［17］ JRWEAVERW，TIMOSHENKOSP，YOUNGDH.Vibration problems in engineering［M］.Princeton：Van Nostrand，1955：329-331.

［18］ NOGAMIT，NOVAK M.Resistanceofsoiltoa horizontally vibrating pile［J］.Earthquake Engineering and Structure Dynamics，1977，5(3)：247-261.