如何提高文科学生学习大学数学的兴趣

2011-01-30刘莉

河北职业教育 2011年12期

刘莉

（德州学院，山东德州 253023）

随着社会经济的迅速发展，社会科学和自然科学与数学更加广泛地紧密结合。在大学文科的一些专业中，也开设了“数理语言学”、“计量经济学”、“教育统计学”等以数学为工具的新的交叉学科，数学素质在大学生的综合素质中占有重要地位。因此培养文科大学生的数学素养已成为社会的需要，其中培养文科学生学习大学数学的浓厚兴趣成为其学好数学的必要前提和学习的关键。

一、通过对数学知识的“基础化”，提高文科学生学习大学数学的兴趣

数学是逻辑性强、连贯性强的一门工具性学科，前面的理论不理解，后面的知识就无法学习。与理科生相比，文科生数学基础较差，数字运算能力、逻辑推理能力和空间想象能力都不如理科生，这些不足造成他们认为数学枯燥难懂，失去兴趣而厌烦上数学课。因此大学数学的理论一定要基础化，注重讲明常识性的概念，会处理简单的计算就可以了，不必缀加抽象的理论和繁琐的证明。不考虑实际情况盲目增加学习的难度，只能让学生望而却步、知难而退。

例如：微分中值定理在高等数学中占有很重要的地位，应用广泛且有一定的技巧性，特别是拉格朗日中值定理和Taylor中值定理。但是定理的内容和证明抽象，构造辅助函数有一定技巧，分析余项时涉及的知识广泛，即使是理工科学生学习时也感到困难，与文科专业课联系极少，在一些经济问题中用到也只是应用简单的公式做近似计算，因此不必介绍中值定理的证明，可以直接给出Taylor公式和麦克劳林公式，让学生记住ex和ln（1+x）的展开式，遇到类似e近似计算会带入展开式，

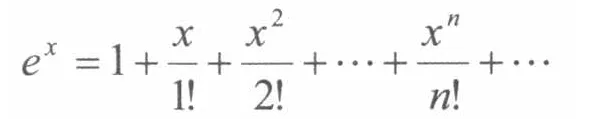
其中x = 1时，利用前10项计算出 e 近似值为2.7182815，误差不超过10-6。简单的代入公式不仅使学生易于掌握，而且得到的结果近似程度较高，具有一定的实用性，才能提高学生的学习兴趣。

二、恰当地融入数学故事，提高文科学生学习大学数学的兴趣

数学家的故事、数学史在大学数学学习中的积极作用也是不容忽视的，如果能适当地融入教学过程，不仅可以提高学生学习枯燥数学理论的兴趣，也能从中感受到数学的重要、数学的美、数学家的科研精神和他们伟大的人格魅力，潜移默化地提高大学生的数学素养。当然，大学数学学习的重点是微积分不是数学史，所以故事引入的人物与事件要简单、恰当、有说服力。例如：讲解微积分基本理论之前，为了说明微积分重要的工具作用，引起学生的重视和学习的兴趣，可以介绍微积分产生的历史背景。17世纪，自然科学界有许多科学问题需要解决，归结成数学问题，大约有四种主要类型：第一类是求物体运动到某一时刻的瞬时速度的问题，第二类是求曲线的切线的问题，第三类是求函数的最大值和最小值问题，第四类问题是求曲线长、曲线围成的面积、曲面围成的体积、物体的重心等。这些问题也就成了促使微积分产生的因素，在学习了微积分的基本内容后，这些问题都能轻而易举地解决。介绍微积分的两位著名奠基人—牛顿和莱布尼兹，介绍牛顿的《流数术》和莱布尼斯的微积分符号。赞美他们对微积分的重要贡献和不断探索的研究精神。引发文科学生对微积分的好奇，提高了文科学生学习大学数学的兴趣。

在讲解曲面积分时，对坐标的曲面积分要转化成二重积分计算，根据曲面的侧面确定二重积分的符号，可以给学生讲解重要的单侧曲面—麦比乌斯带，麦比乌斯带不仅在数学上非常独特，因为它的特殊性质，在一些动画片和智力竞赛中也有提及，其中80后非常爱看的《哆啦a梦》就有这样的情节，哆啦a梦从大口袋中拿给大雄的时光机就是一个麦比乌斯带。学生们没想到枯燥难懂的积分和生活是这样贴近，从而产生了很大的兴趣，课堂气氛变得活跃起来。

三、适时地使用多媒体，提高文科学生学习大学数学的兴趣

近年来，越来越多的课程引入多媒体教学，然而并不是所有的课程所有的内容都适合应用多媒体。因为数学本身的特点，传统的板书教学使学生更容易理解掌握公式应用和定理推导，但是在一些特殊内容的讲解时适当使用多媒体，也有利于学生的直观理解，还可以通过形象的图形提高学生的学习兴趣，起到事半功倍的效果。

例如：二次曲面在多元函数微积分中具有重要作用，特别是计算重积分时，要将二重积分或三重积分化多次积分，确定多次积分中每个积分的上限和下限的依据就是二次曲面，如果不能找到二次曲面所围立体的边界，画不出立体在坐标平面上的投影区域，重积分将无法计算。在黑板上作二次曲面的草图，既耽误时间做出的图形又不准确，如果能利用几何画板在多媒体上作图，不仅直观易于学生理解、提高学习兴趣，而且图形的特殊性质也能一目了然。在积分计算中，适当地利用曲面或立体的对称性等特性，会达到很好的效果。