化学机械抛光中磨粒运动特性离散元仿真研究

谭援强 张 浩 李明军

湘潭大学,湘潭,411105

化学机械抛光中磨粒运动特性离散元仿真研究

谭援强 张 浩 李明军

湘潭大学,湘潭,411105

基于耦合计算流体力学和计算散体力学的方法,利用PFC3D软件模拟了复合磨粒抛光液化学机械抛光(CM P)中抛光液固液两相流的流动行为。通过2个数值实验并将其与他人实验数据进行对比,验证了利用PFC3D软件模拟纳米两相流问题的可行性。对CMP过程进行了数值模拟,解释了一些实验中观测到的现象。

离散元法;化学机械抛光;磨粒流;数值模拟;复合磨粒

0 引言

化学机械抛光(chem ical mechanical polishing,CMP)技术广泛应用于计算机硬盘片、硅晶片超光滑无损伤表面的加工。CMP过程的材料去除机理非常复杂,在很大程度上它仍是一门黑箱技术,需要经验或半经验的数据来优化过程中的各个参数以达到所需的抛光结果[1]。抛光液是CMP的一个关键因素,一般由碱性溶液和磨粒组成,对其流动规律的了解将有助于理解CM P的机理。

Nakamura等[2]建立了一个简单的模型来分析抛光液的润滑条件。Sundararajan等[3]针对工件范围内的抛光液流动情况建立了二维润滑模型,通过求解Reynolds方程得出了抛光液膜厚和流体动压力。但是他们的工作都没有考虑抛光液中磨粒强大的机械冲击。现有实验结果已经表明,晶片表面材料去除率与抛光液中悬浮磨粒的分布有很大的关系[4]。Zettner等[5]利用荧光显像技术研究了CMP流场中磨粒的平均速度和变形率,但是他们的研究完全是经验性的,而且没有给出局部区域离散颗粒的运动特性。Terrell等[6-7]提出并利用增强混合润滑模型(PAM L)研究了抛光液中磨粒速度的分布情况,估计了磨粒运动对材料去除的影响,但PAM L假设抛光液固态相质量分数非常小(0.029),因此回避了多个磨粒间的碰撞行为。当固态相分数较大时,该模型并不适用,利用动量守恒的方法描述磨粒间的碰撞局限性较大。文献[8-9]利用耦合格子Bo ltzmann法和离散元法研究了CMP过程中晶片表面压力分布和磨粒轨迹特性,但模型相对比较简单且与真实的CMP过程有一定差异。此外,在抛光液的选取方面,日本 Toshiba集团半导体公司以及JSR计算精密电子研究实验室的研究人员利用无机粒子(A l2O3)/有机粒子(树脂)组合的复合磨粒抛光液对铝等材料进行了 CM P试验,结果表明,利用这种带有大粒径树脂颗粒的复合抛光液获得的抛光效率更高,晶片表面缺陷更少[10]。

本文采用耦合计算流体力学和计算散体力学的方法,研究复合磨粒抛光液CMP两相流中磨粒的运动特性,利用PFC3D软件对CMP过程中磨粒的运动特性进行模拟,采用Anderson等[11]提出的经典两相流流体方程描述抛光液流体的运动,并采用压力梯度模型[11]实现流体和磨粒间流固耦合力的计算,最后利用离散元法[12]模拟磨粒/磨粒、磨粒/晶片间的碰撞以及磨粒的运动。

1 CM P抛光液连续流体模型

本文作以下合理假设和约定:①抛光液为速度完全展开的牛顿流体;②晶片和抛光垫完全由抛光液隔开,晶片的载荷由产生的流体动压力承担;③CMP过程中,一般认为抛光液的化学反应作用先使晶片表面生成一层软化膜,这层软化膜再由磨粒去除,本文对CMP过程中化学反应的作用不作研究,重点讨论磨粒的机械去除作用;④本文研究的磨粒去除行为属三体磨损行为,对于嵌入抛光垫中的磨粒不作研究;⑤磨粒是抛光液的一部分,自身对流体流动的影响忽略不计;⑥为了简化模型,在计算固液耦合力时,只考虑压力梯度力和流体拽力作用;⑦所采用的简化CMP计算区域均为长方体或带有曲面底边的长方体区域,约定长方体的长边记为长,垂直于纸面的边记为宽,膜厚方向的边记为高。

CMP工艺过程如图1所示。本文的关注区域为通过晶片中心的等速度带,并把这段半弧形区域简化为长方体区域。真实的CMP工艺中,抛光垫和晶片的转速分别经验性地取为150 r/min和100r/min,本文也以此作为标准的CMP工艺速度参数换算到模型中,相对应的抛光垫的速度u为 1.8m/s、晶片的速度 v为0.26m/s[13]。

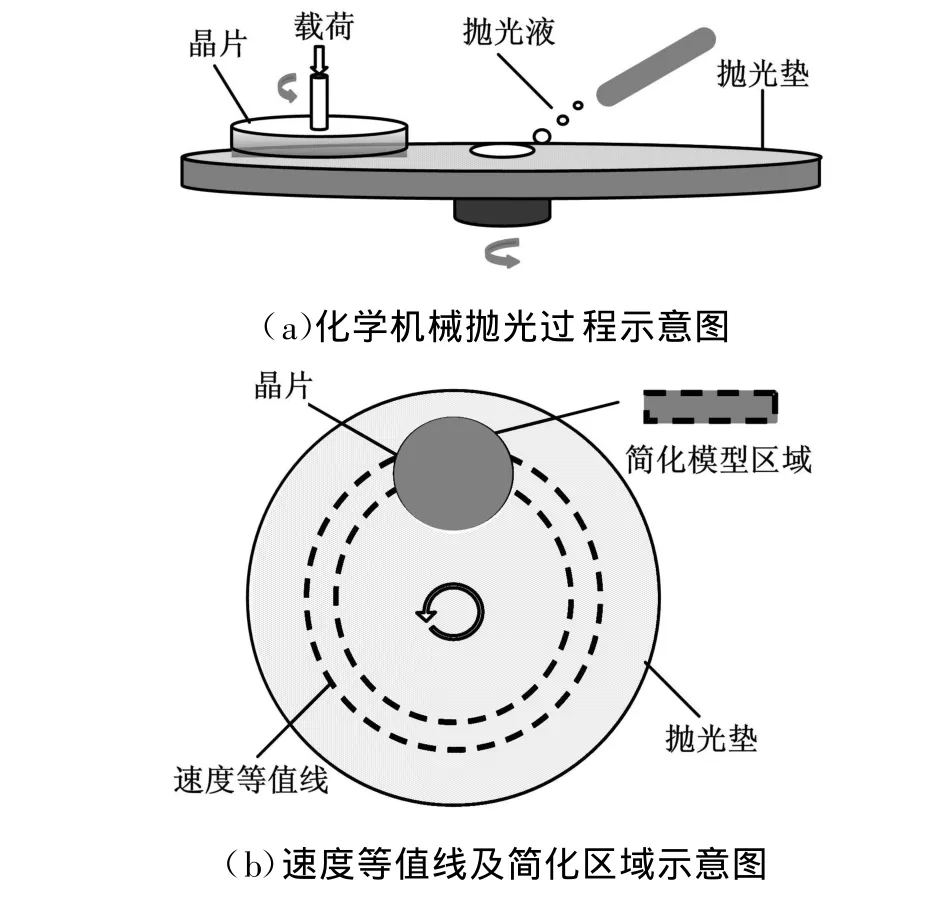
图1 计算区域示意图

本文在Terrell等[6]的模型基础上讨论了磨粒间碰撞作用对材料去除率的影响,因此依然采用文献[6]中所用的简化模型。图2a为二维简化CMP计算区域示意图,计算区域被简化为带有曲面底边的长方体区域,其中,光滑的上表面代表晶片,粗糙的下表面代表抛光垫。在大多数CMP过程中,抛光垫表面被认为较晶片粗糙许多,因此本文中假设晶片表面光滑,利用正弦波曲线代表粗糙的抛光垫表面,曲线方程如下:

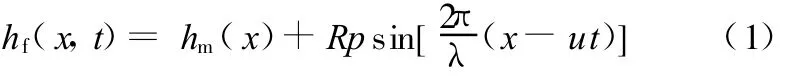
其中,Rp为抛光垫粗糙表面粗糙度;λ为粗糙峰与粗糙峰的间距;t为数值模拟所用时间;x为沿晶片方向的水平位移;h m(x)为平均液膜厚度。

假设抛光垫在晶片表面下连续变化,那么平均液膜厚度只与x有关。基于式(1)构造出新的抛光垫表面,见图2b。

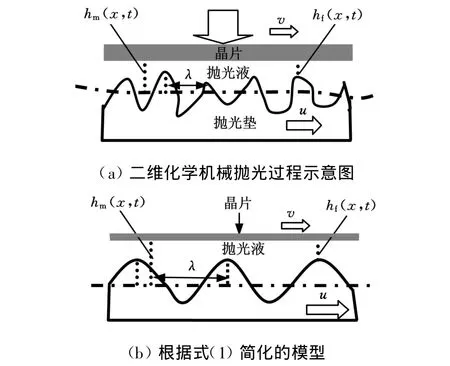
图2 简化区域示意图

基于A nderson等[11]提出的经典两相流模型,本文中用来描述抛光液流动行为的连续性方程和动量方程可表示为

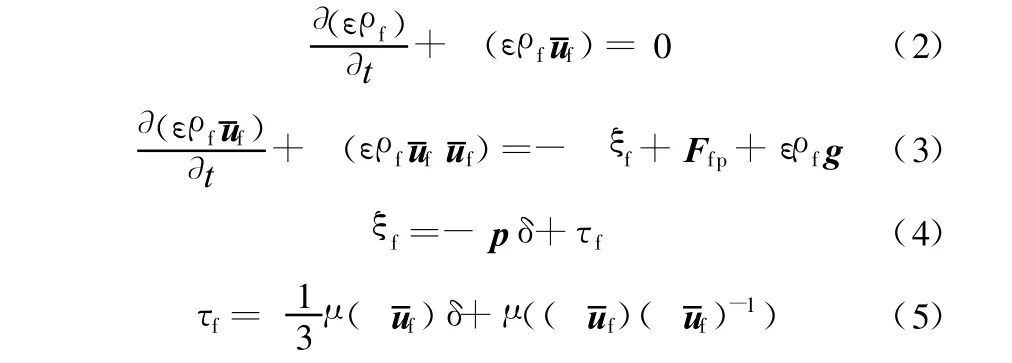
当ε=1、F fp=0时,式(2)和式(3)表示无磨粒纯流体抛光液模型。在研究磨粒运动特性前,本文首先对CMP抛光液的纯流体模型作了数值模拟,模拟结果如图3所示,其中计算区域长为100μm,宽和高均为15μm,其他参数如表1所示[13]。

图3 CMP抛光液纯流体模型的流场

表1 CMP纯流体模型所用参数

从图3中我们可以看到,由于黏性的作用,靠近上下边界的流体几乎与其附近的固体边界同速,计算区域中部的流场沿膜厚方向自下向上呈分层分布。流体计算采用PFC3D软件中的CCFD模块。

2 固液耦合力的计算和离散单元法

2.1 压力梯度模型

每个流体单元上的流固耦合力为

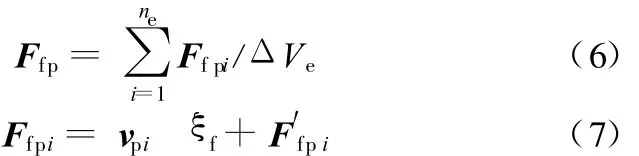
式中,ΔVe为流体单元体积;ne为流体单元个数;Fpi为流体与单个颗粒间的流固耦合力;F′fpi为流体拽力;Ffpi为流体应力张量和颗粒周围点应力张量的和;vpi为颗粒i的速度。

把式(4)代入式(7),并把F′fp i写成拽力εF d i的形式,式(7)可以化为

2.2 本构关系方程

作用在单个颗粒上拽力Fdi的计算公式是由Di Felice[14]提出来的,Di Felice利用一种经验性的拟合法将两相流中作用在单个悬浮颗粒上的拽力表示为

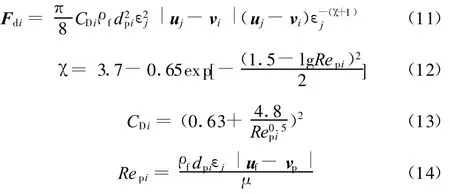
2.3 离散单元法简介

当颗粒间没有发生直接碰撞时,颗粒只受流固耦合力和重力作用(如考虑重力加速度),颗粒的运动可由以下牛顿第二定律描述:

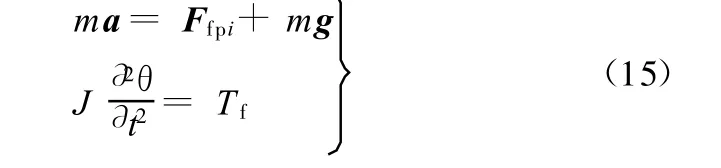
式中,m、J分别为颗粒的质量和转动惯量;Tf为单个颗粒的转矩。

当颗粒间或颗粒与墙间发生直接接触或碰撞时,颗粒之间的接触力用离散单元法[12]计算,离散单元法的思想与分子动力学方法相似,它假设颗粒均为刚体,并使每个颗粒满足运动方程(牛顿第二定律),通过颗粒间的接触作用定律,计算接触力,最后利用迭代的方法求解每个颗粒的运动方程。考虑单元间接触受力后的颗粒运动方程变为

m a=Fc+Ffpi+m g (16)式中,Fc为颗粒间或颗粒与墙碰撞时产生的接触作用力。

本文中,计算接触作用力的模型采用线性模型:

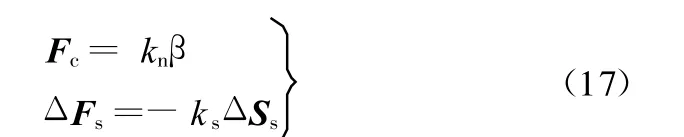
式中,kn、ks分别为法向和切向的刚度系数;β为发生接触时单元间或单元与墙间的“假性重叠量”,用来代替实际接触区域颗粒的小变形;ΔFs为切向接触力增量;ΔSs为切向位移增量。

切向力是以增量的形式给出的。

3 校正数值实验

3.1 与文献[15]中实验的对比

为了验证本文方法模拟纳米两相流体的可行性,首先模拟剪切实验中纳米颗粒的运动行为,并与文献[15]的实验结果数据进行了对比。Shapley等[15]利用激光开普勒测速仪观测了窄缝内两相流体中颗粒相的速度分布。图4a所示为套在一起的2个同心圆缸套,内圈缸套转动,外圈缸套固定,两层缸套夹缝间充满带有纳米级颗粒的流体。为了与Shap ley等[15]的实验进行对比,本文的计算模拟区域如4b所示,其中,上盘固定,下盘自左向右滑动,上下表面均为光滑表面。计算区域长为500μm,宽和高均为 50μm,在计算区域中随机生成800个颗粒,颗粒和流体所用参数如表2所示,其中颗粒密度记为ρs,颗粒平均粒径记为rm。模拟结果如图5所示,图5a中,x轴代表速度,y轴代表颗粒所在位置与窄缝宽度h的比值γ;图5b为颗粒和流体的速度分布矢量图及随机选中颗粒的速度随时间变化情况,短箭头代表颗粒的速度,长箭头代表流体速度,箭头方向与所在位置速度方向相同,箭头长度与速度大小成正比。从图5a中可以看到,颗粒与流体的速度分布基本一致,证明纳米级两相流中的颗粒具有较强的随动性,这与文献[15]的实验数据较一致,说明利用PFC3D软件模拟固液两相流问题是行之有效的。从图5b中也可以看到流体与颗粒速度分布趋势基本相同,而从随机选中颗粒的速度变化曲线可以看到,在模拟开始时颗粒很快加速到与周围流体相同的速度,在随后时间保持不变(固态相分数小,颗粒间无碰撞)。

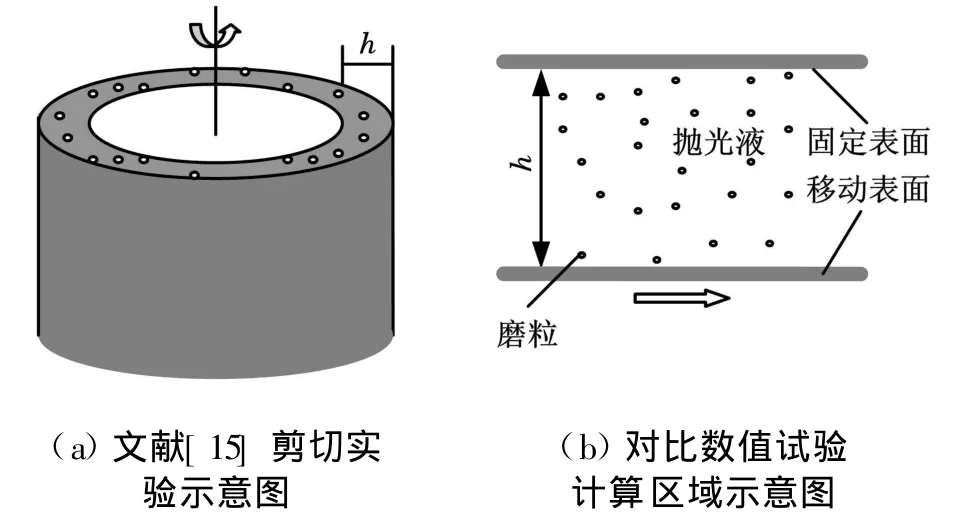
图4 与文献[15]实验的对比

表2 文献[15]对比实验所用参数

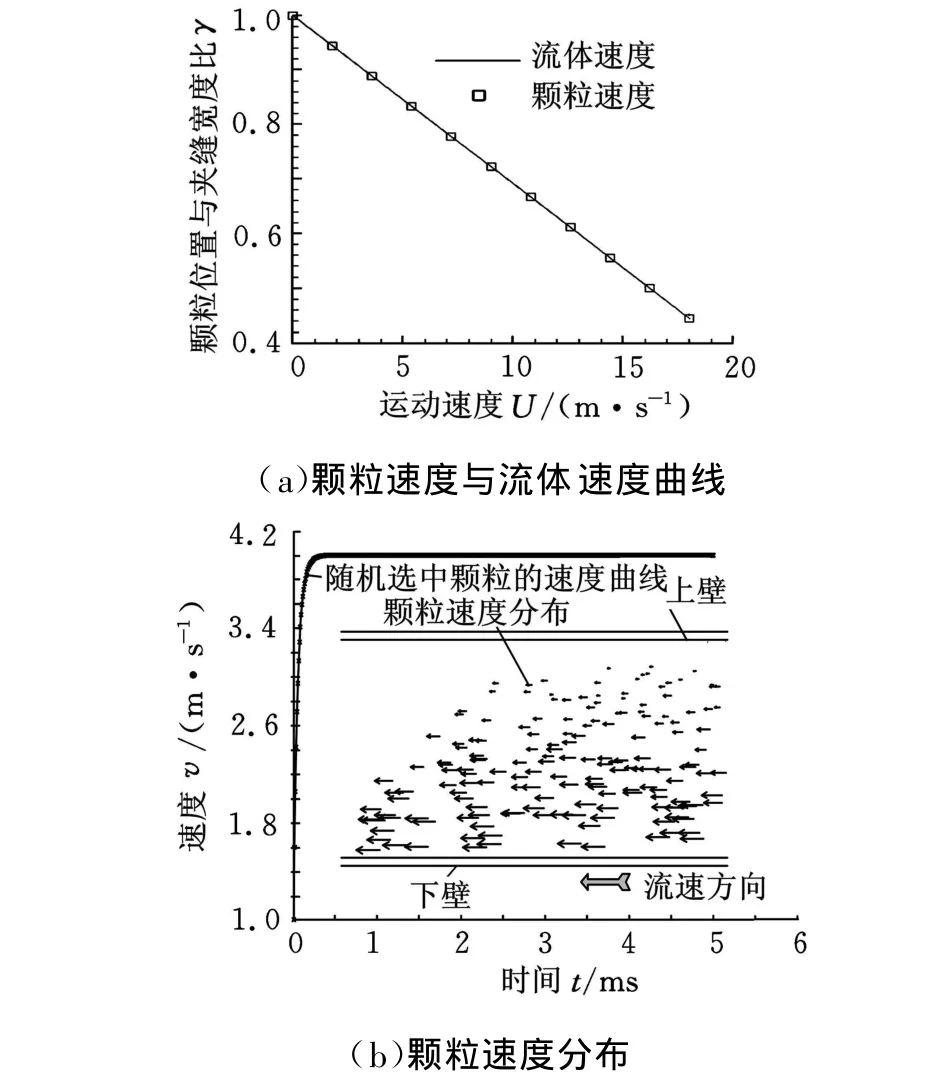
图5 模拟结果与文献[15]中实验结果的对比

3.2 与文献[16]中实验的对比

闫晶等[16]选用荧光显微镜、CCD摄影机及注射泵等对压力驱动纳米固液两相流中纳米颗粒运动进行实时观测。为了与文献[16]的实验进行对比,分别模拟流体平均速度为7.5m/s、9.0m/s、10.5m/s时流体和颗粒的速度分布,其中计算区域长为500μm,宽和高均为 50μm,在计算区域中随机生成800个颗粒,四壁采用不滑移边界,其他参数如表2所示。图6a中,横轴代表颗粒和其周围流体的速度,纵轴代表颗粒所在高度与h的比值。从图6a可以看到,颗粒速度分布基本呈抛物线形分布,颗粒具有较强的随动性,这与闫晶等[16]在实验中得到的结论是一致的,当两相流体速度增加时,颗粒速度也增加,但速度分布趋势不改变。图6b所示为颗粒和流体的速度分布和随机选中颗粒的速度随时间变化情况。图6b中得到的颗粒速度分布趋势也与闫晶等[16]在实验中观测到的现象相同。

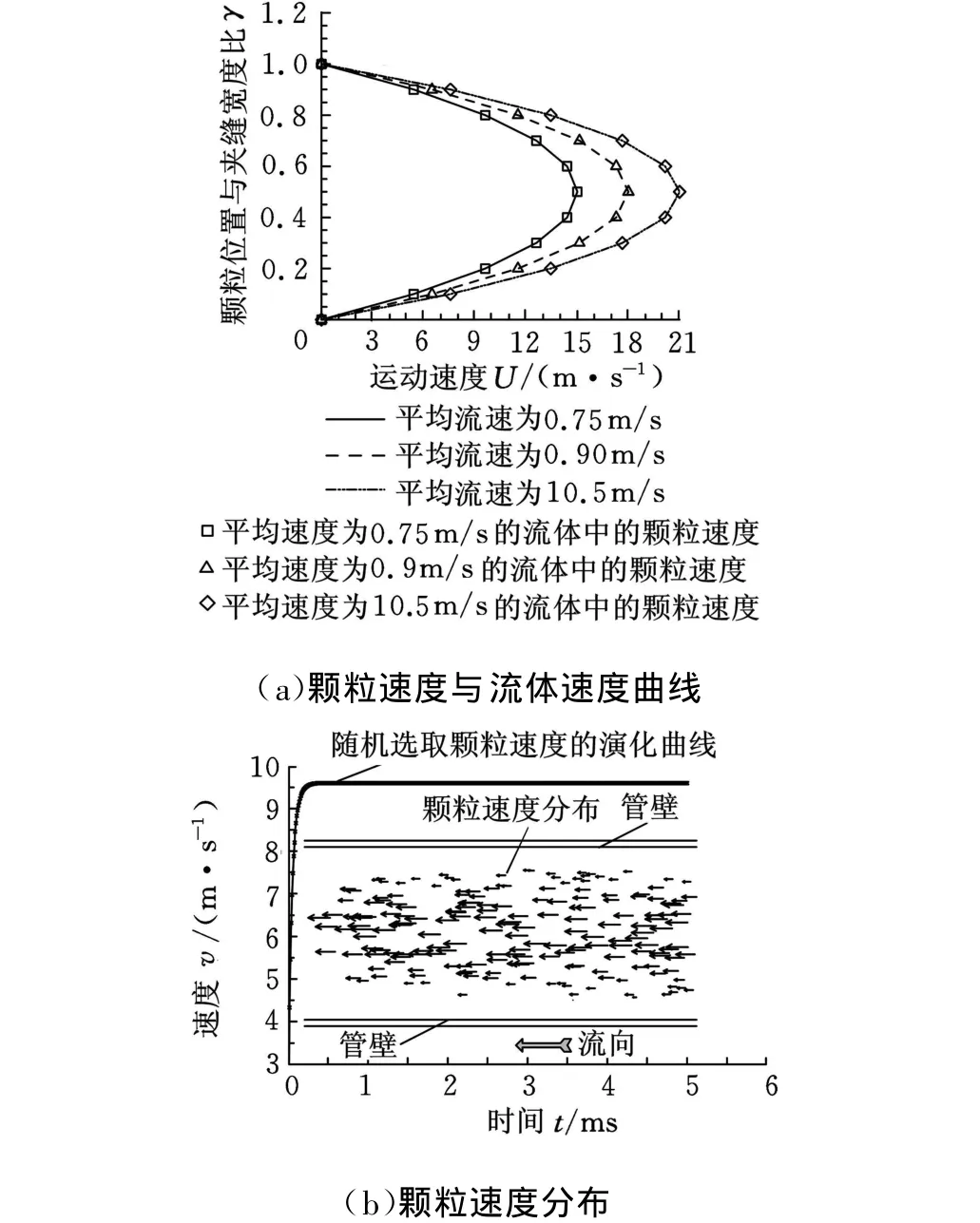
图6 模拟结果与文献[16]中实验结果的对比

数值模拟结果和实验观测数据对比表明,利用PFC3D软件模拟固液两相流问题是行之有效的。本文的数值模拟结果比文献中统计的结果“光滑”得多的原因如下:一是实验中观测难免有误差存在,即便取平均后,结果的波动在所难免;二是就本文的数值模拟而言,颗粒的体积非常小,单个颗粒几乎很难同时跨越2个流体单元,因此它总是与所在流体单元的速度一致。

4 CM P问题模拟

4.1 实验准备

图7的计算区域与图2b的计算区域相同。为了观测磨粒与晶片间的碰撞,模拟中,本文只在“关注磨粒行为区域”即靠近晶片表面的区域生成磨粒;为了防止磨粒走动造成晶片左半段区域接触真空,我们只对右半段晶片即黑色区域所受的非平衡力进行统计。

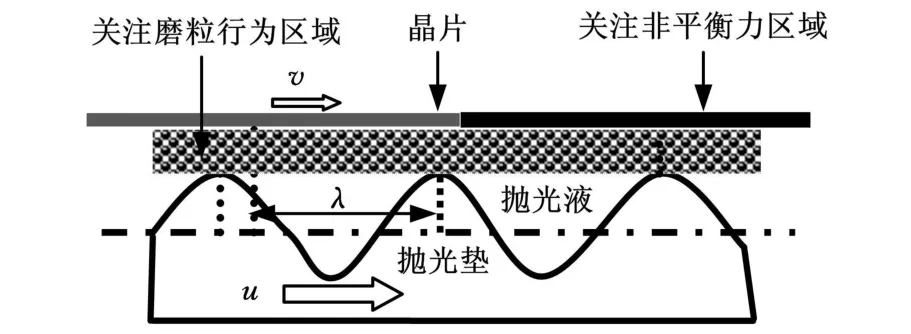
图7 简化计算区域和关注区域示意图

利用PFC3D软件对复合磨粒抛光液[10]进行模拟,首先在流场中生成一颗复合磨粒,得到了单个磨粒在流场中的运动特性;随后又生成数百颗复合磨粒,研究了不同固态相分数、磨粒粒径、抛光垫和晶片转速时晶片所受的非平衡力的变化情况,模拟所用参数见表3。

表3 CMP模拟所用参数

4.2 结果与讨论

图8所示为单个复合磨粒在流场中的运动情况,黑色曲线为磨粒速度随时间的变化曲线。可以看到磨粒在凸凹不平的抛光垫上方运动时,速度总是处于波动的状态,当磨粒向抛光垫波峰移动时,速度也越来越大,如图8所示。因此可以判断,当磨粒运动到抛光垫波峰时,抛光垫波峰流体速度大,磨粒加速,而经过抛光垫波谷时,流体速度相对较小,磨粒减速。这样当晶片表面附近的颗粒较多时,由于磨粒速度不同而发生相互碰撞和挤压,磨粒对晶片表面进行冲击,实现晶片表面材料的去除。

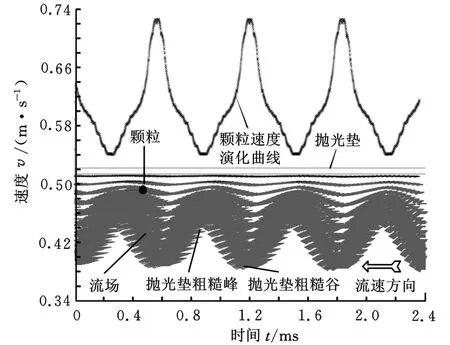
图8 单个复合磨粒在流场中运动

图9给出了500颗磨粒在流场中的运动形态。上方曲线表示随机选中的单个颗粒速度随时间的变化,可以看到速度曲线出现细微波动,这是由磨粒间的相互碰撞造成的。从图9我们还可以看到,磨粒流剪切作用明显,下方磨粒的速度明显大于上方磨粒的速度。图10中,离散点表示磨粒固态相分数 α为 0.16、u=1.8m/s和 v=0.26 m/s时晶片在垂直表面方向所受的非平衡力,可以看到晶片所受的不平衡力先升后降,并出现明显波动,这是由磨粒流本身的离散性造成的。为了比较数据的变化趋势,对离散数据进行二次拟合,细曲线为离散点的拟合曲线,下文讨论的非平衡力演变曲线均为拟合处理后的光滑曲线。

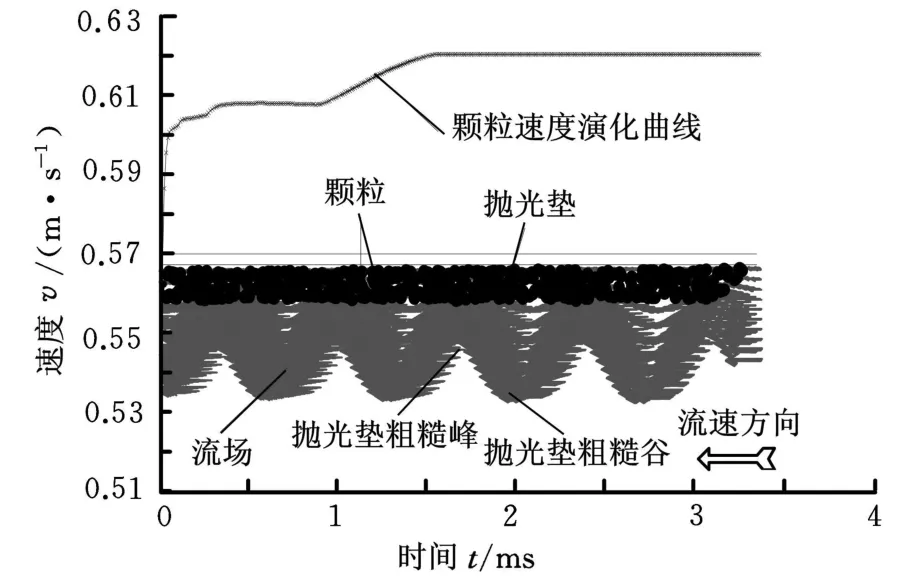
图9 关注区域随机生成500个磨粒

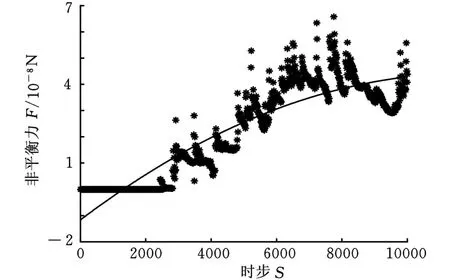
图10 晶片所受不平衡力及其拟合曲线

图11所示为u=1.8m/s和v=0.26m/s,固态相分数 α为 0.04、0.08、0.12、0.16、0.20 时晶片所受的非平衡力拟合曲线,可以看到,随着固态相分数的增大,晶片所受非平衡力明显变大。这是由于固态相分数变大,关注区域磨粒数目增多,磨粒间碰撞频率加大,因而增大了磨粒流对计算区域上表面晶片的挤压作用。

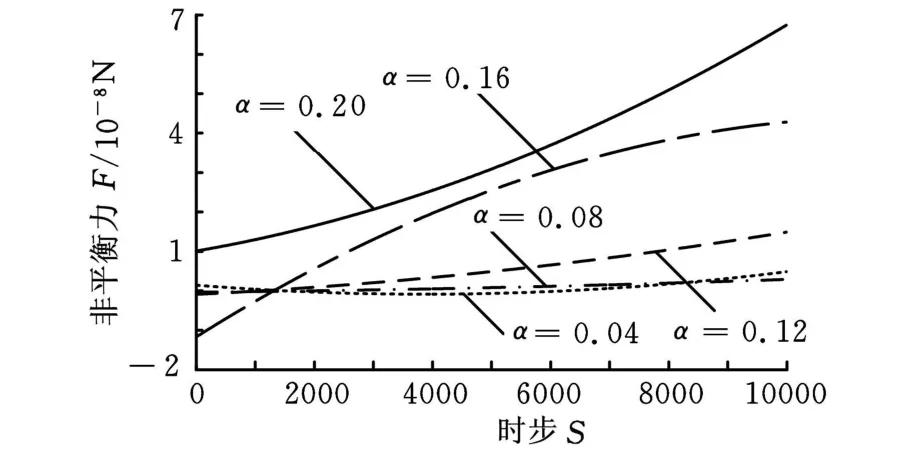
图11 不同固态相分数下非平衡力拟合曲线

图12所示为u=1.8m/s和v=0.26m/s,固态相分数为 0.16,颗粒粒径分别为 800nm、1000nm、1200nm和1400nm时晶片所受非平衡力拟合曲线。可以看到,颗粒粒径为800nm时,晶片受力几乎为零,表示几乎没有磨粒与晶片表面发生碰撞;而当颗粒粒径由800nm增大到1200nm,晶片所受非平衡力增大,当颗粒粒径继续增大到1400nm时,非平衡力反而减小。如果要生成一定固态相分数的颗粒,当颗粒粒径增大时,生成颗粒数目则变少,因此颗粒间碰撞次数减小,碰撞晶片表面的概率也降低,但由于颗粒体积变大,磨粒单次冲击晶片表面的力度也变大,从粒径为1200nm时的曲线可以看出,当粒径较大时,个别磨粒冲击晶片力度很大,其他时候则很小,这样容易造成晶片表面损伤。

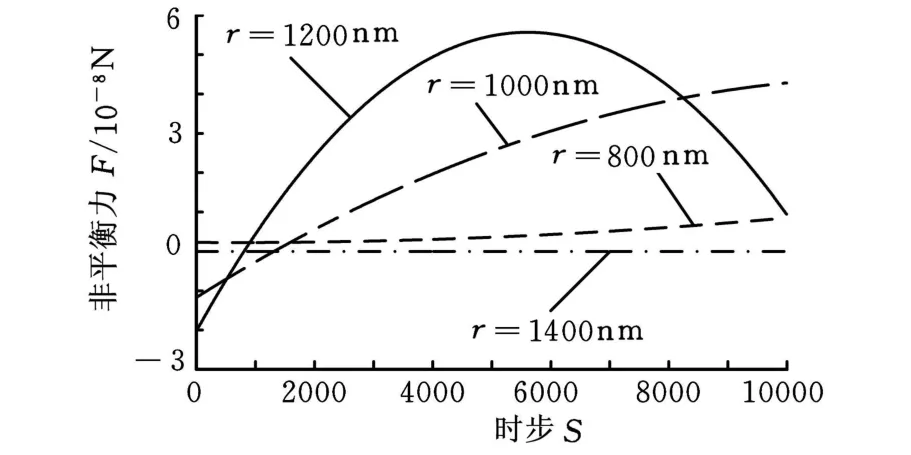
图12 不同粒径下非平衡力拟合曲线

图13所示为固态相分数为0.16,v=0,u分别为 0.9m/s、1.8m/s、2.7m/s时,晶片所受的非平衡力拟合曲线,可以看到,晶片所受非平衡力随抛光垫转速增加而增大,这可以理解为晶片和抛光垫的速度差增大,颗粒流剪切作用增强。

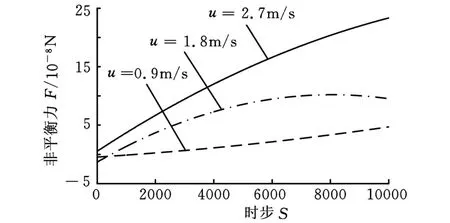
图13 u不同时的非平衡力拟合曲线(v=0)

图14中,实线为固态相分数为0.16,v=0,u别为 0.9m/s、1.8m/s、2.7m/s时,晶片所受的非平衡力拟合曲线;虚线为v=0.26m/s,抛光垫转速为 0.9m/s、1.8m/s、2.7m/s时,晶片所受的非平衡力拟合曲线。分别对比相同抛光垫转速、不同晶片速度下的非平衡力曲线可以发现,晶片转速的变化对非平衡力的影响较抛光垫小得多,晶片转动与不转动相比,使晶片所受非平衡力变小,这是由于晶片与抛光垫同方向转动,晶片转动使得上下表面速度差变小造成的。图15为固态相分数为0.2时,不同抛光垫、晶片转速对晶片所受非平衡力的影响,我们分别给出当u=1.8m/s,v分别为0.13m/s、0.26m/s、0.39m/s和 v=0.26m/s,u 分别为 0.9m/s、1.8m/s、2.7m/s的 5种组合时晶片所受非平衡力变化拟合曲线。从图15中我们可以得到同图13一样的结论,即u和v的速度差越大,晶片所受的非平衡力也越大。

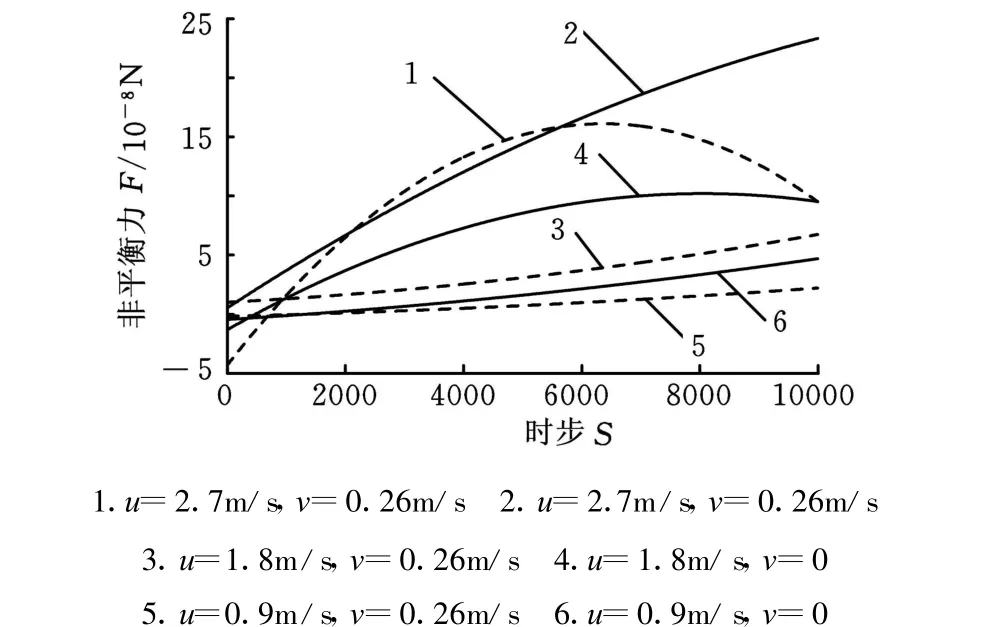
图14 u和v不同时的非平衡力拟合曲线

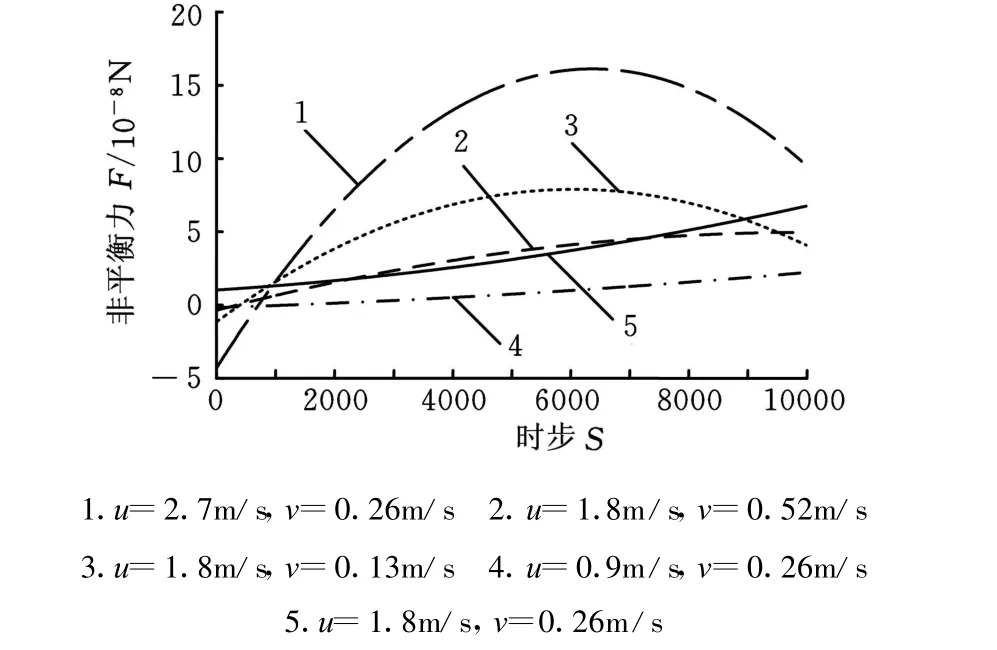
图15 u和v不同时的非平衡力拟合曲线

5 结论

(1)颗粒在抛光垫粗糙峰波峰时速度最大,在波谷时速度最小。

(2)晶片表面附近的磨粒流存在明显的剪切现象,剪切作用越大,晶片所受非平衡力也越大,去除效率越高。

(3)当固态相分数从0.04增大到0.20时,区域固态相分数越大,磨粒碰撞几率也越大,碰撞次数越多,去除效率越高。

(4)当颗粒粒径由800nm增大到1200nm时,晶片所受非平衡力越来越大;当颗粒粒径由1200nm继续增大到1400nm时,非平衡力减小。

(5)一定范围内,晶片与抛光垫表面速度差越大,磨粒流剪切作用越强,去除效率越高。

[1] Xu Jin,Luo Jianbin,Lu Xinchun,et al.Progress in Materia l Removal Mechanisms of Surface Po lishing w ith U ltra Precision[J].Chinese Sci.Bulletin,2004,49(16):1687-1693.

[2] Nakamura T,Akamastu K,A rakawa N.A Bow l Feed and Double Sides Polishing for Silicon Wafer for V LSI[J].Bull Japan Soc.of Prec.Eng.,1985,19(2):125-135.

[3] Sundararajan S,Thakurta G D,Schwendendeman D W,etal.Two-dimensional Wafer-scale Mechanical Planarization Model Based on Lubrication Theory and Mass Transport[J].Journal o f the Electrochemical Society,1999,46(2):761-766.

[4] Luo J F.Effec ts of Abrasive Size Distribution in Chem ical Mechanical Planarization:Modeling and Verification[C]//IEEE Trans.on Semiconductor Manu facturing,2003,16(3):469-476.

[5] Zettner C M,Yoda M.Direct V isualization of Particle Dynamics in Model CM PGeometries[C]//Proceeding of Materia ls Research Society Sym posium.Pittsburgh,PA,2001:M 6.6.1-M 6.6.6.

[6] Terrell E J,H iggs C F.A Modeling Approach for Predicting the Abrasive Particle Motion during Chem ical Mechanica l Po lishing[J].Journal of T ribology,2007,129(4):933-941.

[7] Terrell E J,H iggs C F.A Particle-augmented Mixed Lubrication Modeling Approach to Predicting Chem ical Mechanica l Polishing[J].Journal o f T ribology,2009,131(1):012201-10.

[8] Zhang H ao,Tan Yuanqiang,Li M ingjun.A Numerical Simulation o f Motion of Particles under the Wafer in CMP[C]//2008 International Con ference on Computer Science and Softw are Engineering.Wuhan,China,2008:31-34.

[9] 谭援强,张浩,李明军.利用三维格子 Boltzmann法研CMP中压力分布[J].润滑与密封,2009(7):18-22.

[10] A rm iniS,W helan C M,Maexb K,et al.Composite Polymer-core Silica-shell Abrasive Particles during Oxide CM P:a Defectivity Study[J].Journal of the Elec trochemical Society,2007,154(8):H 667-H 671.

[11] Anderson T B,Jackson R.A Fluid Mechanical Description of Fluidized Beds.Equations o f Motion[J].Industrial and Engineering Chem istry Fundamental,1967,6(4):527-539.

[12] Cundall P A.A Computer Model for Simu lating Progressive Large Scale Movements in Blocky System[C]//Proc.Symp.Int.Soc.Rock Mechanics.Rotterdam,1971:8-12.

[13] Haosheng C,Jiang L,Darong C,et al.Nano Particles's Behavior in Non-New tonian Slurry in Mechanical Process o f CMP[J].Tribo logy Letters,2006,24(3):179-186.

[14] Di Felice R.The Voidage Function for Fluid-particle Interaction Systems[J].International Journal on Multiphase Flow,1994,20(1):153-159.

[15] Shap ley N C,A rmstrong R C,Brow n R A.Laser Doppler Velocimetry Measurements of Particle Velocity Fluctuations in a Concentrated Suspension[J].Journal of Rheo logy,2002,46(1):241-272.

[16] 闫晶,雒建斌,徐学锋.纳米颗粒固液二相流实时观测[J].纳米技术与精密工程,2005(6):117-121.

Modeling and Simu lation of Abrasive Flow in Chem ical Mechanical Polishing Using Discrete Element Method

Tan Yuanqiang Zhang Hao Li Mingjun
Xiangtan University,Xiangtan,Hunan,411105

According to coup ling com putational fluid dynamics and com putational granular media mechanicsmethod,themotion of abrasive flow in CMPw ith composite particleswas simulated using discrete elementmethod.With PFC3D so ftware,a two-phase flow m odel that p redicted the kinematics and trajectory of theabrasive particleswasbuiltherein,two verification simulationswere conducted to dem onstrate the capability of the currentm ethod to solve nano-size two-phase flow problems.Finally,the CM P geometry simu lations were conducted,some phenomenon observed in the experiments were exp lained.

discrete elementmethod;chemicalmechanical polishing(CMP);abrasive flow;numerical sim u lation;composite particle

TH 16

1004—132X(2011)05—0597—07

2010—04—09

国家自然科学基金资助项目(50875224);教育部新世纪人才项目(NCET:06-0708);教育部博士学科点专项科研基金资助项目(20070530003)

(编辑 张 洋)

谭援强,男,1966年生。湘潭大学机械工程学院教授、博士研究生导师。研究方向为超精密加工及其摩擦学。张 浩,男,1984年生。湘潭大学机械工程学院博士研究生。李明军,男,1968年生。湘潭大学数学与计算科学学院教授、博士研究生导师。