数学史与认知教育

张偲

（重庆教育学院经济与贸易系，重庆400067）

数学是什么？中学数学教学大纲中有一个定义：数学是研究空间形式和数量关系的科学。也就是说，数学是刻划客观规律的科学。这是否可以看作关于“数学是什么”的一个完善的定义呢？

首先，我们要简单的回顾一下西方世界的数学史。在经历了古希腊时代的芝诺（Zeno，公元前五世纪）、欧多克斯（Eudoxus，公元前408－355）、欧几里得（Euclid，公元前323年－前283年）、阿基米德（Archimedes，公元前287－212）等前人们的努力与发展，数学主要是以其兼具严谨逻辑与广泛应用的欧式几何学出现在世人面前的。

随着时间的推演，特别是伟大的德国数学家、哲学家莱布尼兹（Leibniz，1646－1716）与人类科学史上的巨人牛顿（Newton，1642－1727）“发明”的古典微积分，让分析学取代了统治数学上千年的刚性欧氏几何学成为数学的“霸主”，至今，已有300余年历史。

所以伊夫斯认为数学史就是一部微积分史，并在他的名著《数学史概论》中说：“第一本微积分课本出版于1696年，它是由洛必达写的。”洛必达是法国数学家（1661—1704年），高数中求分子分母同时趋于零的分式极限的“洛必达法则”，就是以他的名字命名的。

微积分首次传入中国，是160年后的1859年，李善兰与英国来华学者伟烈亚力（A.Wylie）合作翻译并出版了美国人罗密司（E.Loomis）的新作《解析几何与微积分学》，题名为《代微积拾级》，共18卷。

“微分”和“积分”源于成语“积微成著”，《荀子·大略》：“夫尽小者大，积微成著，德至者色泽洽，行尽而声问远。”

洛必达的贡献其实不是“洛必达法则”，该法则是约翰·伯努利于1694年告诉洛必达的。洛必达功绩在于撰写了世界上第一本系统的微积分教程《用于理解曲线的无穷小分析》。这本书深受欧几里得和阿基米德公理化方法的影响，堪称追随古典的范例，它以定义和公理为出发点，再给出运算的基本法则和例子。

对于洛比达法则，有这样一段有趣的轶事，据说是高斯提出来的：“无穷小不是零，但又不是确定的数，那么，两个不确定的数相除，何以得到确定的数（这里高斯指的就是导数）？”。所以，从第一个理论上给出了无理数和连续性纯粹算术定义的德国数学家戴德金（Julius Dedekind，1831—1916）留下了这样的墓志铭：“上帝发明了整数，然后就把其他留给了人类”。作为实数理论主要奠基人之一，戴德金并不是故弄玄虚，因为他所生活的那个年代，数学正经历着一次革命性的大爆炸：19世纪数学三大发现。这三大发现是以黎曼微分几何为典型代表的非欧几何；阿贝尔与伽罗华引领的代数革命——群论；以及康托尔、威尔斯特拉斯、戴德金奠基的实数理论。

实数理论的革命性发展，为当时已经危机重重的经典微积分提供了一次重生并再次引领数学发展的契机。

微积分号称三百多年来最伟大的数学，俨然成了凌驾于几何、代数等分支学科的数学带头大哥，然而当狄里克雷（Dirichlet）教授提出的狄里克雷函数却让经典微积分对之无可奈何。让经典微积分感到恐惧的不仅仅是这样极端“病态”的函数，在人们施展微积分这门武功去对付各种自然科学中的问题时也会显得心有余而力不足。例如，当我们试图将积分与极限交换顺序时，极限号始终无法穿越那令人望而生畏的S。事实上，一个黎曼可积的函数序列｛fn｝即使是收敛的，其极限却可能是个不可积函数，此时讨论等式

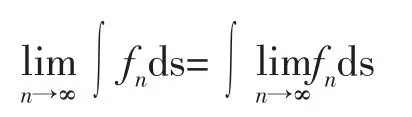
这个困扰数学家们多年的计算问题，在聪明的法国数学家勒贝格（1875～1941）Lebesgue看来这是黎曼积分定义出现了缺陷：黎曼和的取值一旦取到了非连续或者非可数间断的“病态”定义域上，就变得没有了说服力。于是勒贝格果断的放弃了经典的积分定义模式，从点集拓扑学出发，并抛弃了内外测度夹逼相等建立可测集的经典测度理论（这种办法在高维拓扑结构中受很大限制），而是以值域为考察对象，运用布尔代数的概念，建立起了勒贝格积分。不仅让分析学重振雄风，更让概率论焕发出前所未有的耀眼光芒。

我们现在让时间倒退到17世纪，德·梅勒在骰子赌博中，因故需要中止赌博，赌博双方各出的30个金币的赌资要靠对胜负的预测进行分配，但不知用什么样的比例分配才算合理。德·梅勒写信向数学家帕斯卡请教，帕斯卡与费尔马通过书信往来共同研究这个问题，于是一个新的数学分支——概率论诞生了。这就是说，概率论源于赌博。

虽然概率论深入到了科学的几乎每一个角落，但直到19世纪下半叶，关于概率的一般定义始终未能明确化和严格化。在形式主义数学为主流的时代，这一理论远远落后于其他数学分支的发展。1900年，希尔伯特在世界数学家大会上提出了建立概率论公理化体系的问题，随后庞加莱、波莱尔及伯恩斯坦等一流的数学家致力于希尔伯特所倡导的概率论公理化体系的研究，其第一个公理化体系出自伯恩斯坦，而把概率论与测度论相联系的重要思想则源于拓扑学大师波莱尔。

时间又回到了勒贝格所生活的年代，他所建立的测度与积分理论为概率论公理体系奠定了理论基础，随着对大数定律的深入研究，概率论与测度论的内在联系越来越现出端倪。大数定律中的收敛性与测度论中的几乎处处收敛及依测度收敛异曲同工。基于这样的缘故，柯尔莫哥洛夫在其《概率论基础》一书中以测度论方法第一次给出了概率论一套严密的公理体系，此公理体系一经提出，迅速得到了公认。柯尔莫哥洛夫的理论是概率论发展史上的一个里程碑，它为现代概率论的发展打下了坚实的基础，也为其赢得了20世纪最伟大的三位数学家的美誉——另外两位是德国数学家希尔伯特与法国数学家庞加莱。

以微积分为主体的分析数学的历史暂时回顾到这里了。那么，回到最开始那个问题：数学是什么？笔者读研究生的时候在一次讲座上也曾向中国科学院应用数学所的林群院士提出过类似的疑问：中国人跟十九世纪的数学三大发现没有关系，跟二十世纪前半叶的泛函与微分拓扑学的突飞猛进也没什么瓜葛，但是我们一样生产出了原子弹、氢弹、卫星、三峡大坝。请问数学到底是什么？有没有用？

林院士当时并没有直接回答笔者的疑问，而是举了三个西方发达国家在科学史与工程史上的例子。

例1：在二次世界大战前，世界上没有一个飞行员敢做垂直于地面的圆周飞行，直到后来一位前苏联数学家从数学上证明了上述飞行的可行性，最终才由前苏联的飞行员完成了第一次飞行。

例2：1985年的诺贝尔化学奖获得者霍普特曼（Hauptman）其实不是个化学家。早在上个世纪初，化学家们就知道，当X－射线穿过晶体时，光线碰到晶体中的原子而发生散射或衍射。当他们把胶卷置于晶体的后面，X－射线会使随原子位置而变动的衍射图案处的胶卷变黑。化学家们为难的是，他们无法准确地确定晶体中原子的位置。原因在于X－射线也是波，它们有震幅和相位。这个衍射图只能探清X－射线的震幅，却不能探测相位。四十多年后的1950年前后，霍普特曼意识到，这件事可以转换为一个纯粹的数学问题。果然，他借助100多年前的傅里叶（Fourier）分析，找出了决定相位的方法，并进一步确定了晶体的几何。结晶学家只见过物理现象的影子，霍普特曼却利用古典数学从影子来再现实际的现象。也许有些人不知道，郝特曼一生只上过一门化学课，即大学一年级的化学，可他却因此项工作获得了诺贝尔化学奖。

例3：柯朗与希尔伯特（Hilbert）合著的书《数学物理方法》（该书实际由柯朗所写，有中译本）在早期只有数学家们感兴趣，物理学家们不屑一顾。可是，当物理学家们对苦思苦想了很多年而不得其解的方程无可奈何，不得不求助于数学家时，发现这本书中的理论比他们所期望的解答还要好。在这之前更加经典的典故是阿尔伯特·爱因斯坦在研究广义相对论陷入找不到广义力矩的瓶颈之时，从他的同胞、早已去世半个多世纪的大数学家黎曼那里找到了答案；物理学诺贝尔奖获得者杨振宁从数学高斯奖获得者陈省身那里找到了“纤维丛”理论。

在笔者熟悉的经济学领域，数学可以为经济金融建模，模型的求解过程所引发的数学问题恰恰需要回归纯粹数学领域来解决。譬如，为了研究相关产业间的投入需求与产出水平的关系的技术性最优解，里昂惕夫（Leontief）教授提出了著名的投入——产出模型。在实际的模型中，产业部门极多，投入系数矩阵非常庞大。所谓里昂惕夫逆矩阵的求解，在不借助大型计算机的情况下，本身就是一个计算数学难题。1990年，福里德里克.V.沃在《通过幂级数求里昂惕夫矩阵的逆》一文中指出，在开放模型中，投入系数矩阵每一列的元素和都小于1，其高次幂趋于零矩阵，故里昂惕夫逆阵有特殊解法。

数学的发展从来就不是单纯靠内力推动的。纳什（Nash）与伊藤（Ito）都是真正数学大师，而他们的研究——Nash原理与Ito定理分别在经济学的博弈论与金融学的资产定价方面有非常广泛的应用与极其深远的影响。但是，他们起初都不是为了应用而是凭借单纯的兴趣进行他们的数学研究的：除了博弈论，纳什在代数几何和非线性理论等诸多纯粹数学领域都有着非凡的造诣，伊藤清则明确的说过“纯粹数学中严谨的论证与优美的结构深深地吸引了我”。。

这些例子告诉了我们什么呢？数学决不仅仅是一种方法，一门“技艺”，她更是一种思想、一种理念。数学教会我们一种科学的思维方法，赋予我们一个严谨的思辩头脑。著名的数学家、冯诺依曼的助手哈尔莫斯（Halmos）讲过这样一句话：“具备一定的数学修养比具备一定量的数学知识要重要得多。”从这个意义上说，数学教育的根本目的并不在于让你掌握多少数学知识，最重要的在于培养你一双敏锐的眼睛，善于从纷乱复杂的自然现象中发现有规律的东西，学会以丰富的科学语言、严谨的思辩头脑和科学的研究模式去探索世界的奥秘，进而作出发明和创造。这便是认知教育的核心理念。

［1］W.Rudin，Functional Analysis，McGraw－Hill Book Company，1973.

［2］江泽坚，孙善利.泛函分析［M］.北京：高等教育出版社，1994.

［3］陈省身，陈维桓.微分几何讲义［M］.北京：北京大学出版社，1983.

［4］陈希孺.数理统计引论［M］.北京：科学出版社，2007.

［5］P.Halmos.Measure Theory［M］.北京：世界图书出版公司，2007.

［6］钟开莱.概率论教程［M］.北京：机械工业出版社，2010.

［7］A.H.Kolmogorov.函数论与泛函分析初步［M］.北京：高等教育出版社，2006.

［8］S.Karlin.随机过程初级教程［M］.北京：人民邮电出版社，2007.

［9］王梓坤.概率论基础及其应用［M］.北京：北京师范大学出版社，2007.

［10］E.T.Bell，Men of Mathematics［M］.北京：商务印书馆，1993.