模糊聚类算法在案例教学系统中的应用研究

刘先锋，李 宁

（湖南师范大学数学与计算机科学学院，湖南长沙410081）

1 引言

在基于案例推理的系统中，由于案例的增加，使得案例库变得异常庞大，学习者检索数据效率低，并且智能性较差。这里应用数据挖掘中的模糊聚类对学习者和案例库分别进行聚类，使具有不同学习模式的学生分为一类，针对这样的学生，系统可以智能的给他们分配一组相似的案例进行学习，从而达到个性化教学，弥补了传统的案例教学的缺陷。

2 模糊聚类

模糊聚类分析是模糊集理论与传统的聚类分析相结合的分析方法，它克服了硬聚类分析在划分对象时“非此即彼”的缺点。常用的模糊聚类方法有：①基于模糊等价矩阵的聚类方法（传递闭包法、Bool矩阵法）；②基于模糊相似矩阵的直接聚类法（直接聚类法、最大树法、编网法）；③基于目标函数的模糊聚类分析法。这三种方法各有利弊，本文结合实际的案例分析采用传递闭包法对学生和案例分别进行模糊聚类。模糊聚类分析的具体步骤：对聚类要素进行数据预处理，建立模糊相似矩阵，采用传递闭包方法进行聚类，选择最佳聚类方案。

2.1 对聚类要素进行数据预处理

现实生活中事物之间的相似性很难用“相似”或者“不相似”来定性，引入模糊逻辑对事物进行分类更符合客观事实，假设共有5个学生，分别是u1，u2，u3，u4，u5，对它们进行数据预处理如下表所示：

表1 学生信息表

测试成绩以最近一次考试的成绩作为依据，其中分优、良、中、及格、不及格；学习风格分为：行动型、反省型、理论型、实际型、讨论型；媒体偏好分为：文字、图片、声音、视频以及多种媒体的混合；学习倾向分为：记忆型、理解型、领会型、应用型、综合型。每一项分别用1-5这五个数字来表示。

2.2 求模糊相似关系矩阵

模糊相似矩阵应该满足自反性和对称性，方法有很多，夹角余弦法、最大最小法、算术平均最小法、兰氏距离法、绝对值减数法等，在这里选择常用的绝对值减数法。公式如下：

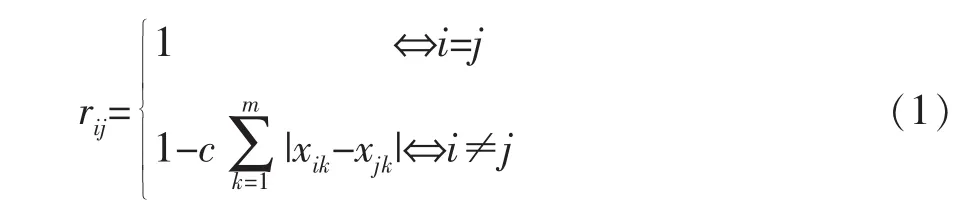
其中c为适当选取数，使0≦rij≦1。

其中选取c＝0.1，m＝4，i，j＝1，2，3，4，5。由此得出相似矩阵R如下：

2.3 聚类

当λ＝1时，分类为5类，｛u1｝｛u2｝｛u3｝｛u4｝｛u5｝，当λ＝0.8时，分为4类，｛u1，u3｝｛u2｝｛u4｝｛u5｝，当λ＝0.6时，分为3类，｛u1，u3｝｛u2｝｛u4，u5｝，当λ＝0.5时，分为2类，｛u1，u3，u4，u5｝｛u2｝，当λ＝1时，分为1类，｛u1，u2，u3，u4，u5｝。

可以看出针对不同的λ值会有一个不同的分类组合，那么如何才能确定最佳阀值呢？可以用一种F-统计量的方法确定λ的最佳值，公式如下：

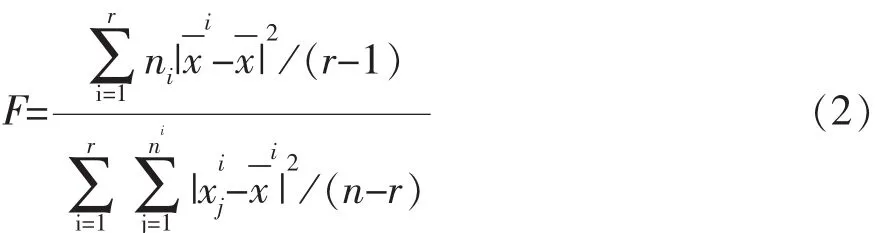
通过F统计量公式可以计算出最佳的学习者分类，对学习者建立分类以后，对于同一个学习组的成员有相似的学习习惯，学习兴趣，学习模式，因此便于教师针对这一组学生因材施教。

3 对案例库中的案例进行模糊聚类

对于案例库中的案例除了按类别，科目不同进行分类存储以外，又进一步结合案例的特有属性对同一科目的众多案例采用传递闭包法进行聚类。对某个案例描述T1，根据其属性的不同，分为具体—抽象程度，难—易程度，呈现方式，要求学生掌握的水平等几个领域。把同一领域的众多案例分成三个等级，一级案例，二级案例，三级案例，级数越高，案例的复杂度和抽象度越大，根据学生的认知水平给学生推荐适合的等级案例，以指导学生学习。

4 学生综合能力评测

学生每学完一个案例之后，对其进行能力测试，计算出他的综合能力值，根据其综合能力值提供与其自身相适应的下一组案例继续学习，克服以前的ITS中对学生评价的缺点，从而为教师提供决策支持。由于影响学生综合能力的因素是多方面的，各因素的权重分配较为均衡的情况，此时可以采用将诸因素分解成若干个层次进行研究。

4.1 多层次模糊变换理论

将因素集U＝｛u1，u2，u3，…un｝分成若干个组U1，U2，…UK（1≤K≤n），使得

称U＝｛U1，U2，…UK｝为一级因素集。不妨设称其为二级因素集。设评判集V＝｛v1，v2，…vm｝，对二级因素集的ni个因素进行单因素评判，建立模糊映射i），于是得到评判矩阵Ri，不妨设的权重为则可以求得综合评判为其中b（1）j由模型（M∧，∨）确定。对于一级因素U＝｛U1，U2，…UK｝作综合评判，不妨设权重A＝（a1，a2，…ak），总评判矩阵为R＝（B1，B2，…BK）T，按模型M（∧，∨）得到综合评判B＝A°R＝（b1，b2，…bm）∈F（V）。

4.2 在案例教学为核心的ITS中的应用

一级因素集U＝｛U1识记，U2理解，U3应用综合｝，其中Ui（i＝1，2，3，4）又由更加具体的因素所决定。U的权重为A。其中U1＝｛对案例内容的理解，识记的方法，识记案例材料的性质，识记的目的｝，U2＝｛案例的具体程度，原有知识经验背景的影响，主动理解的意识与策略｝，U3＝｛学生对知识的理解水平与巩固程度，学生的智力水平，课题的性质，动机与情绪｝，C1＝C2＝C3＝｛很好c1，一般c2，较差c3，差c4｝，通过对Ui分别设定矩阵Ri，表示各因素的权重，Ui的第一级评判为Bi＝Ai，归一化得：，由上述第一级评判结果可以得到第二级评判矩阵R＝（，，）T，通过计算得出R＝（0.46，0.36，0.2，0.09），U的权重A＝（0.3，0.5，0.2），则B＝A°R＝（0.46，0.36，0.2，0.09），从而认定该生很好的成份为46%，一般的成份为36%，较差的成份为20%，差的成份为9%，因此系统判断该生综合能力为很好，可以推荐他及与他在一个小组的同学先学习高级案例，即从综合运用等实例中总结出定理和概念。相反，如果测出该生综合能力较差，或者差，可以首先推荐他及与他在一个小组的同学学习一级案例，即从概念和定理等识记理解的案例开始学习，从而达到因材施教。

5 总结

本文通过引入模糊聚类知识优化了以案例推理技术为指导的CBR学习系统，针对不同的学习小组提供等级相适应的学习案例，达到了个性化学习的目的，减少了学习者面对众多的案例盲目选择的弊端。

［1］刘浩淼，徐从富，何俊.基于模糊聚类的歌曲智能推荐方法研究［J］.计算机工程与设计.2009，（10）：23－27.

［2］卢秋根.模糊聚类算法的研究与实现［J］.电脑知识与技术.2008，（9）：1987－1990.

［3］张莉.基于模糊聚类的案例聚类算法研究［J］.教育与教学研究.2009，（4）：4

［4］Lizhen Liu，Lei Chen，Cuixia Shi，HaiChen.The Study of Collaborative LearningGroupingStrategy in IntelligentTutoring System［J］.International Conference on Computer Supported CooperativeWork in Design.2010，（14）：642－646

［5］YanWei.GaoQi..The Study ofa NovelMixed FCMClustering and Using in the Index of Engine CBR Design System［J］.International Conference on Computer Modeling and Simulation.2010：398－399

［6］刘甘娜，杨烜.ITS中学生水平的模糊综合评价模型［J］.西安交通大学学报.1995，（4）：8－12