某卫星微振动建模与仿真

蒋国伟，周徐斌，申军烽，顾亦磊，杜 冬，孔祥森

（上海卫星工程研究所，上海 200240）

0 引言

微振动是指航天器在轨运行期间，星上运动部件周期性运动或因变轨、冷热交变等因素引发的扰动使星体产生一种幅值较小、频率较高的颤振响应。对高精度航天器，这种微振动将严重影响有效载荷指向精度、稳定度和成像质量，降低分辨率等重要性能指标[1-2]，因此，在高精度航天器研制过程中，需要特别考虑微振动的影响。

本文借鉴国内外研究经验，分析研究了某卫星面临的微振动力学环境，建立了一种刚柔耦合多体动力学微振动仿真模型，通过地面微振动试验验证仿真模型后，再利用仿真模型预测卫星在轨的微振动响应以及微振动传递特性。

1 卫星微振动力学环境分析

卫星微振动力学环境主要包括星载各类转动部件高速转动、大型可控构件驱动机构工作、大型柔性构件进出阴影冷热交变诱发，以及变轨调姿期间推力器工作等产生的微振动[2]。

某卫星是我国第二代静止轨道气象卫星（如图1所示），装载有对微振动极为敏感的高精度遥感探测仪。在轨工作过程中，载荷扫描镜驱动机构、飞轮、陀螺等运动部件的运动将会引起卫星微振动，影响卫星载荷的指向精度和成像质量。

大量研究表明，动量轮（反作用轮）工作时产生的扰动是影响航天器成像质量的主要扰动源[3]，Eyerman和Shea[3]等人认为动量轮等高速转动部件对成像质量的影响最大；结合Bialke、Melody、Kim、Castles和James[4-8]等人及“哈勃”望远镜[9]的研究成果，通过对图1所示卫星的力学环境的分析可以推测，引发该卫星微振动的主要因素有：飞轮、垂直探测仪和扫描辐射计的运动部件的转动或平动。

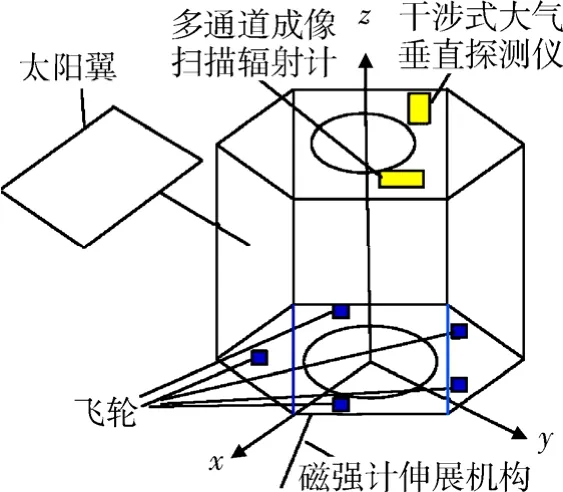
图 1 某卫星结构示意图Fig.1 Schematic diagram of a satellite’s structure

根据微振动力学环境或者分析环境对象的不同，微振动力学模型的建立也应不同。现阶段，某卫星的微振动分析主要考虑星上运动部件引发的瞬态加速度和稳态加速度[10]，即针对运动部件扰动引起的微振动响应建立机械动力学微振动仿真模型。

2 微振动力学模型建模

目前，比较成熟的集成建模软件系统有MIT的DOCS和NASA的IME，其中，IME更具实用性，其主要分析模块之一为颤振分析（Jitter Analysis）模块[11-12]。本文参考IME颤振分析建模思路，根据某卫星微振动力学环境特点，建立卫星机械动力学微振动仿真模型。

经过对星上扰动源特点的分析，确定了某卫星的建模思路：先建立部件级扰动力学模型，然后将部件级扰动力学模型与整星模型耦合建模。为准确描述卫星微振动及其传递特性，将扰动源设定为刚性体、其他部分作为柔性体建模，建立卫星刚柔耦合动力学微振动仿真模型。具体建模过程如图2所示。

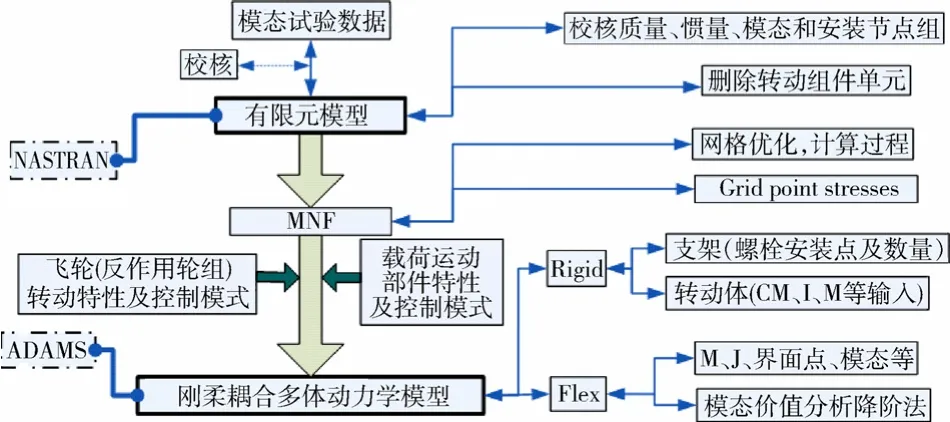
图 2 微振动力学模型建立过程Fig.2 The modeling procedure of micro-vibration dynamics

在建模过程中，需要考虑的主要因素如下：

1）飞轮扰动主要是由于轮子质量分布不均引起的静不平衡和动不平衡造成的，扰动模型要准确描述扰动的实际情况[13]。在飞轮实际安装位置处建立飞轮数学模型，根据飞轮研制单位提供的飞轮数据赋予数学模型实际飞轮的物理特性。飞轮的扰动参数包括频率范围、幅值级别、作用在结构上的位置和方向[2]，其中，幅值级别可用飞轮静不平衡量和动不平衡量，即质心偏心及惯性积来描述。

2）振源运动部件为刚性体，传递路径为柔性体。振源运动部件间产生的激励和冲击通过柔性体传递，会相互影响并使振源的激励方向发生微小变化，导致响应在卫星坐标系三轴上的分量也实时发生变化，即：在内扰动与外扰动同时存在的情况下，颤振模型能反映振源实时变化的扰动输出。

3）整星有限元模型利用模态试验数据修正，并转换为多体动力学模型；再利用模态价值分析降阶法，根据模态价值大小选取适当的模态，以便更为快速和准确地计算微振动在卫星各处的响应大小。

4）在ADAMS软件仿真平台上，星体上转动部件的约束主要分为两类。非旋转部分与星体之间的螺栓连接选择柔性连接衬套来模拟，旋转部分和非旋转部分之间的旋转连接选择旋转副来模拟。

5）针对星上运动部件的驱动控制，为更准确描述实际运动情况，利用STEP嵌套函数以实际运动部件工作模式编写仿真控制模式。

为了进一步验证整星动力学模型的正确性，分别计算ADAMS软件平台上的刚柔耦合多体动力学模型（微振动力学模型）与PATRAN软件平台上整星有限元模型的质量、惯量，见图3。校核结果如表1所示。

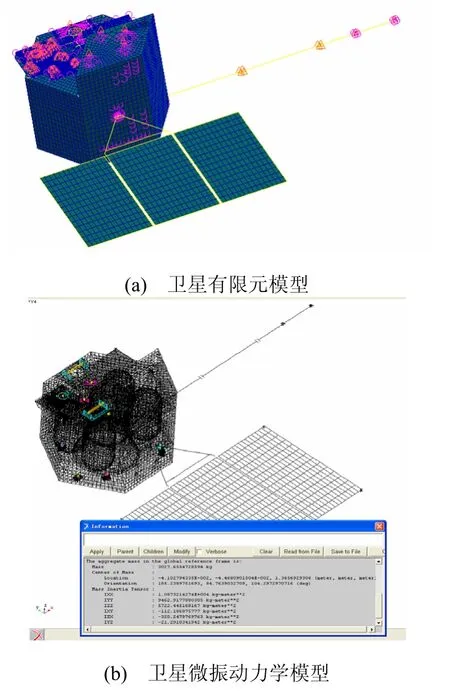
图3 卫星有限元模型与微振动力学模型Fig.3 The finite element model and micro-vibration dynamics model of the satellite

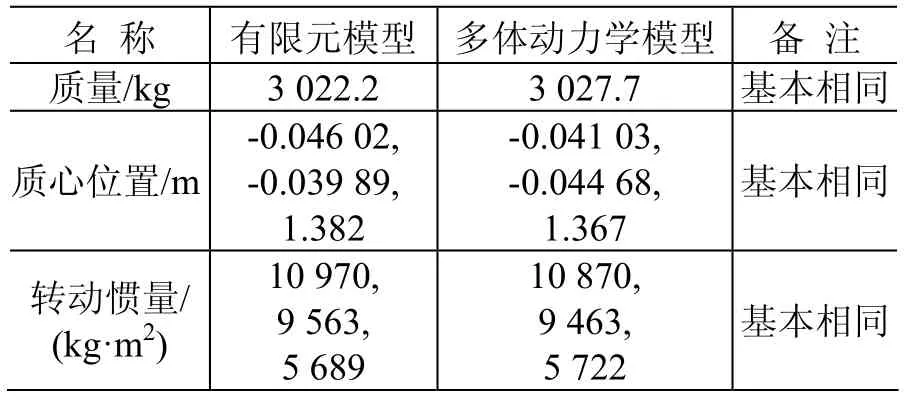
表1 模型信息对比Table 1 Comparison between the finite element model and the micro-vibration dynamics model

由表1可知，在质量、质心和转动惯量等方面，卫星刚柔耦合多体动力学模型的计算结果与有限元模型的基本一致，可以推断卫星刚柔耦合多体动力学模型能较为准确地反映卫星动力学特性。

3 地面微振动试验与仿真分析

高精度航天器微振动力学环境极其复杂，通常仅能做部分地面试验验证，需要在有限的试验的基础上，依靠理论建模和仿真分析手段对微振动响应幅值及频谱分布进行分析和评估[1]。因此，为了进一步验证仿真模型的正确性，进行了地面微振动试验，根据地面试验数据与仿真数据的对比结果，分析了仿真模型对物理模型的仿真程度和准确度。

3.1 地面微振动试验

地面微振动试验中，卫星配备了试验用动量轮1个及其支架，其他飞轮及载荷均不工作；太阳电池阵和磁强计伸展机构不装星，卫星不充推进剂工质。微振动地面试验内容及结果见表2。

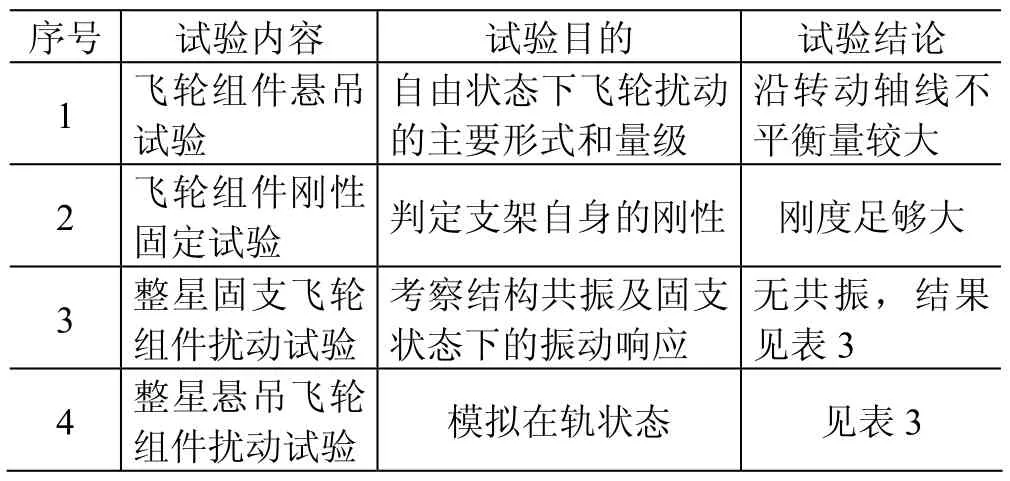
表2 试验工况及试验结果Table 2 Cases and results of micro-vibration tests

整星悬吊飞轮组件扰动试验中，为了使卫星在微振动测试中获得准自由态配置[10]，采用高性能纤维丝吊索将卫星吊起悬在空中；而整星固支飞轮组件扰动试验是将卫星固支在水平振动台上。试验中，卫星z轴均与重力加速度方向一致。控制飞轮以3200 r/min稳速转动，记录各传感器三个方向的响应。传感器粘贴位置如图4所示，由于试验条件的原因，部分测点故障无法取得数据，但基本上获得了传递途径上x、z向峰值振动响应，测试结果见表3。

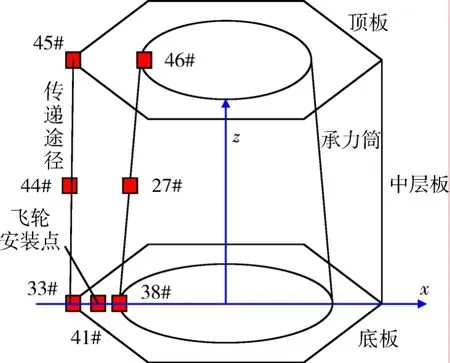
图4 传感器位置示意图Fig.4 Position of the sensors

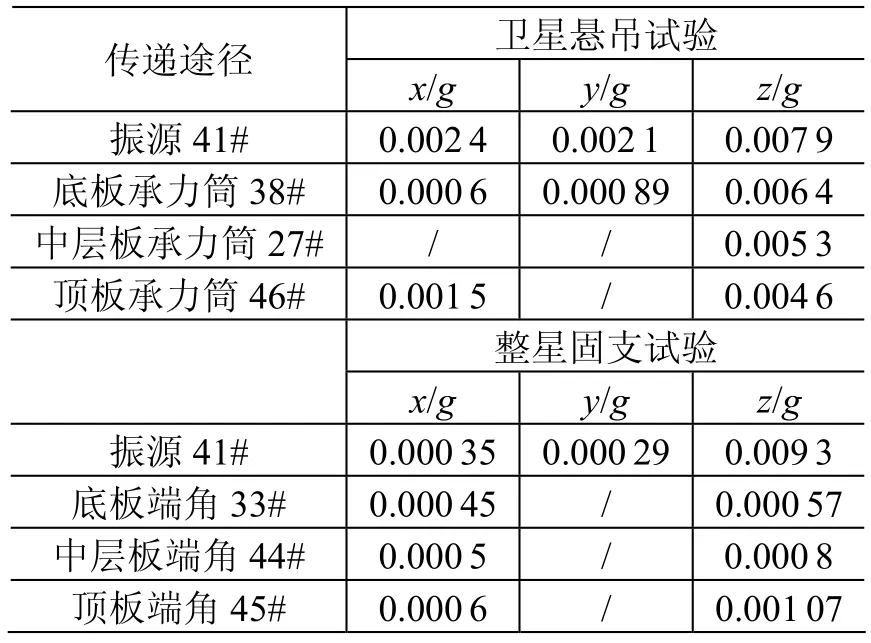
表3 试验结果Table 3 Results of the tests

3.2 微振动仿真试验与分析

3.2.1 仿真试验

在仿真试验中，先参考地面试验卫星技术状态修正仿真模型，其中飞轮不平衡量输入根据“飞轮组件”地面试验数据调整；然后简化试验的边界条件，将卫星动力学模型固支在重力环境下来模拟整星地面固支试验；将卫星在轨动力学模型仿真地面悬吊试验，并参考试验测点位置即传感器粘贴位置，在仿真模型上取相应位置点的响应数据，如图4所示。

3.2.2 试验数据与仿真数据比较

1）试验数据与仿真数据对比分析

试验数据与仿真数据见表4和表5。虽然试验数据略微不足，但从表中数据可以看出，在振源处及传递路径上，仿真数值与试验数据较为吻合。

2）传递路径变化分析

由表4和表5的数据可知，仿真数据与试验数据在传递路径上的表现基本一致，且有一个共同的现象，即响应传递过程中底板到中层板之间存在响应稍微放大的现象，这也与卫星振动试验中的响应传递特性一致。这同时也表明了在一定程度上仿真模型能表现出卫星微振动传输特性。

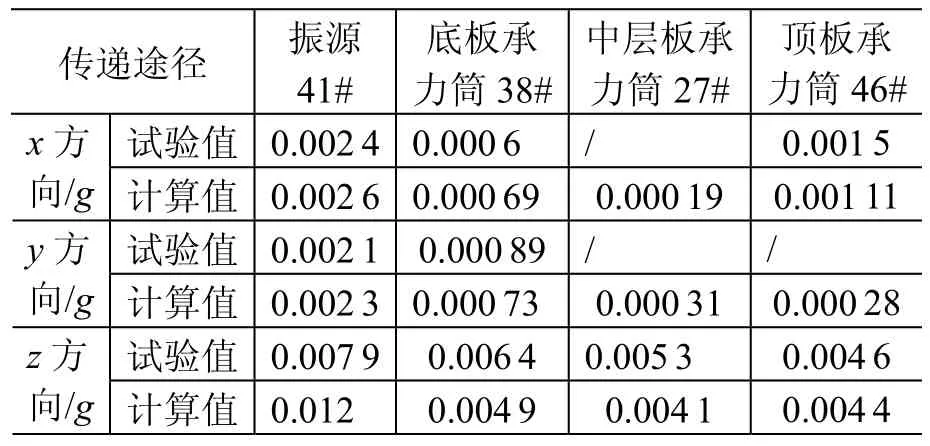
表4 悬吊试验Table 4 Comparison between suspension tests and the simulation

表5 固支试验Table 5 Comparison between tests of fixed support and the simulation

由于受试验条件、试验设备等方面的限制，试验数据较为欠缺，但是所获得的仿真结果仍在一定程度上与微振动试验数据及响应传递变化趋势是较为吻合的。由此可以推断某卫星刚柔耦合微振动力学模型及其仿真方法是较为准确的，在一定程度上可以有效反映卫星微振动及其传输特性。

4 在轨工况仿真与分析

卫星在轨工况定义为所有运动部件同时工作，其目的是获取在轨最恶劣工况下卫星各处的微振动响应情况。卫星运动部件的工作状态是：飞轮转速3000 r/s；扫描辐射计为地球全圆盘常规成像模式；垂直探测仪为中小尺度探测模式；动镜驱动机构为光程差±4 mm模式；太阳翼展开状态，处于0度位置；磁强计展开状态。

经仿真分析，得到飞轮安装点处的响应最大，其值约为0.01～0.06 g；对于载荷部件安装处，其响应值在0.002～0.006 g之间；对于结构特殊位置，其响应值在0.001～0.007 g之间。具体数值及位置如图5和图6所示。

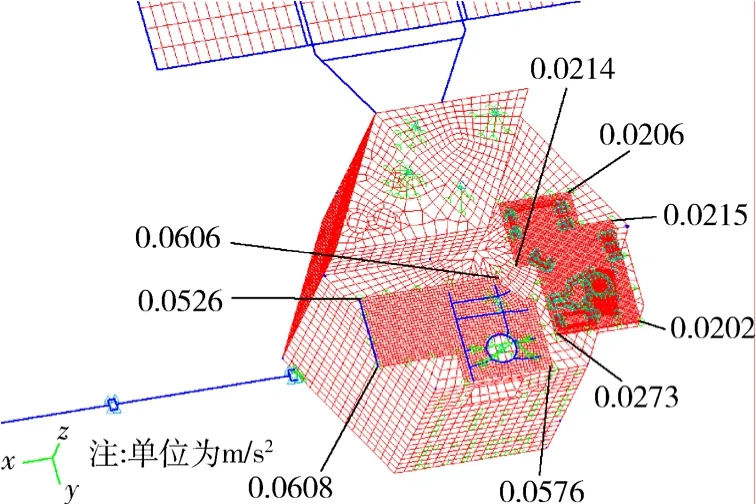
图5 载荷板响应Fig.5 The response of payload setting

图6 卫星结构响应Fig.6 The response of the satellite’s structure

从仿真结果可以看出，底部飞轮引起响应最大，但是经过结构本身的阻尼作用，使得响应在传到载荷板处时已经衰减较多。

5 结论

本文借鉴国内外研究经验，分析了某卫星微振动力学环境，参考IME微振动分析建模思路，建立了一种卫星刚柔耦合微振动力学仿真模型，并开展地面微振动试验验证。验证结果表明，仿真模型能较为准确地仿真卫星微振动响应及其传递特性。通过仿真计算预测卫星在轨微振动响应，在探究卫星微振动力学环境的同时，为载荷的减振方案设计及其研制提供了参考，也为高精度航天器微振动研究探索了一种思路。

（References）

[1]杨雷, 庞世伟, 曲广吉.高精度航天器微振动集成建模与综合评估技术——进展综述与研究思路[C]∥全国结构动力学学术研讨会, 2007

[2]庞世伟, 杨雷, 曲广吉.高精度航天器微振动建模与评估技术最近进展[J].强度与环境.2007, 34(6)Pang Shiwei, Yang Lei, Qu Guangji.New development of micro-vibration integrated modeling and assessment technology for high performance spacecraft[J].Structure& Environment Engineering, 2007, 34(6)

[3]Eyerman C E, Shea J F.A systems engineering approach to disturbance minimization for spacecraft utilizing controlled structures technology, MIT SERC Report#2-90[R],1990

[4]Bialke B.A compilation of reaction wheel induced spacecraft disturbances[C]Proceeding of the 20thAnnual AAS Guidance and Control Conference, 1997

[5]Melody J W.Discrete-frequency and broadband reaction wheel disturbance models[G].Interoffice Memorandum 3411-95-200csi, JPL, 1995-06

[6]Kim Y.Thermal creak induced dynamics of space structures[D].PhD Thesis, MIT, 1999

[7]Collins S A.Multi-axis analog adaptive feed-forward cancellation of cryocooler vibration[D].PhD Thesis,MIT, 1994

[8]Castles S, Cygnarowicz T, Boyle R.NASA/IGSFC cryocooler development program[R], 1996

[9]Wie B, Liu Qiang, Bauer F.Classical and robust H∞control redesign for the Hubble space telescope[C]AIAA∥Guidance and Aviation Conference, 1992-08

[10]赵伟.航天器微振动环境分析与测量技术发展[J].航天器环境工程, 2006, 23(4): 210-214 Zhao Wei.Analysis on micro-vibration environment of spacecraft and measurement technology[J].Spacecraft Environment Engineering, 2006, 23(4):210-214

[11]Stone C M, Haltery C, Medina J.The JWST integrated modeling environment[C]∥Proceedings of IEEE Aerospace Conference, 2004

[12]Miller D W, de Weck O L, Mosier G E.Framework for multidisciplinary integrated modeling and analysis of space telescopes[J].SPIE, 2002

[13]张振华, 杨雷, 庞世伟.高精度航天器微振动力学环境分析[J].航天器环境工程, 2009, 26(6):528-534 Zhang Zhenhua, Yang Lei, Pang Shiwei.Jitter environment analyzing for micro-precision spacecraft[J].Spacecraft Environment Engineering, 2009, 26(6): 528-534