圆锥曲线焦点弦的新视角

玉邴图

(广南县第一中学，云南广南663300)

经过圆锥曲线焦点且被圆锥曲线截得的线段叫做圆锥曲线焦点弦。它是一个非常重要的几何量，也是高考的重点和热点，长考不衰，视角常变，题型多姿多彩，可谓考试长青树。此类题型，涉及知识面广，前几年的高考或竞赛题型仅仅与弦的倾斜角或斜率有关，而近两年来，视角更宽阔了，常常将向量的有关知识与焦点弦倾斜角、长度以及圆锥曲线离心率联系起来，且有一定难度，作为高考解析几何压轴题，旨在考查考生的逻辑推理能力和的综合运算能力，此类题考生失分严重。故值得我们深入总结和分析研究，为此，本文介绍圆焦点弦的一些向量性质，并说明它们的应用，供读者参考。

对于焦点弦长度与斜率或倾斜角的关系，文献［1］介绍了如下结论。

引理 过横向型圆锥曲线焦点F作斜率是k或倾斜角为θ的弦AB，离心率是e，焦点到相应准线的距离为p，则

如果从共线向量的角度研究，可得到如下的重要结论。

定理1 经过横向型圆锥曲线焦点F作倾斜角为θ的弦AB，e是离心率，焦点到相应准线的距离为p，若，(对于椭圆、抛物线和A，B两点在双曲线同一分支上时，与方向相反，λ＜0;对于A，B两点在双曲线的两个分支上时，与方向相同，λ＞0)，则

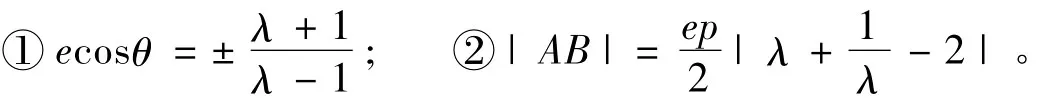
证明 设E是与焦点F相应的准线和对称轴的交点，不妨以有向直线EF所在直线为x轴，F为原点建立直角坐标系，则焦点为F(0，0)，直线AFB的方程为y=kx (1)

①设P(x，y)是圆锥曲线上的一点，它到准线的距离为d，则由圆锥曲线定义知|PF|=ed，由此可得圆锥曲线方程为

设 A(x1，y1) ，B(x2，y2) ，因为 F(0，0)，则由条件和方程(1)得

如果从向量数量积的角度研究，可得到如下的重要结论。

定理2 经过横向型圆锥曲线焦点F作倾斜角为θ的弦AB，e是离心率，焦点到相应准线的距离为p，若，(对于椭圆、抛物线和A，B两点在双曲线的同一分支上时，方向相反，λ＜0;A，B两点在双曲线的两个分支上时，与方向相同，λ＞0)则

将方程(3)的两根之积代入(6)化简得

由定理1和定理2，又可得到如下有趣的结论。

定理3 AB是经过横向型圆锥曲线焦点F的弦，e是离心率，焦点到相应准线的距离为p，若

证明 设弦AB的倾斜角为θ，则由题意及定理1①和定理2①得

定理4 经过横向型圆锥曲线焦点F作倾斜角为θ的弦AB，e是离心率，焦点F到相应准线L的距离为p，L与对称轴的交点为E，若EA和EB的斜率之积为λ，则

证明 不妨以有向直线EF所在直线为x轴，F为原点建立直角坐标系，则焦点为F(0，0)，直线AFB的方程为

设P(x，y)是圆锥曲线上的一点，它到准线的距离为d，则由圆锥曲线定义知|PF|=ed，由此可得圆锥

曲线方程为

设 A(x1，y1) ，B(x2，y2) ，因为 E(－ p，0)，则由题意得

下面我们看这几个定理的应用。

例3(2008年高考全国卷Ⅱ第16题)F是抛物线y2=4x的焦点，经过F且斜率为1的直线交抛物线于A，B两点，求的值。

解 因为e=1，tanθ=k=1，即θ=450，由定理1①得或为所求。

解(1)因为θ=600，λ =－2，由定理1①得。因为(不合题意，舍去)，所以椭圆的离心率

［1］ 玉邴图.一个换算关系的完善［J］．数学通报，2002，(2):21．