群作用下的Khintchine回归定理

王磊杰

(文山学院数理系，云南文山663000)

1898年庞加莱给出庞加莱回归定理，从那时起，回归性就是动力系统研究的重要内容，之后人们给出了庞加莱回归定理的各种各样的推广。1934年Khintchine给出了著名的Khintchine回归定理。至今，回归性仍然是动力系统研究当中的重要内容。

1 基本概念与定理

定义1.1 设X是任意一个集合，B是X的一个σ代数，m是B上的测度，则(X，B，m)称为一个测度空间。若m(X)＜∞，则称(X，B，m)为有限测度空间，否则称为无限测度空间;特别的，若m(X)=1，则称为概率空间。

定义1.2 设(X1，B1，m1)，(X1，B2，m1)是测度空间，映射T:X1→X2称为可测的，指T－1B2⊂B1;映射T:X1→X2称为保测的，指对∀B∈B2，有m1(T－1B)=m2(B);映射T:X1→X2称为可逆的，指T是双射，且T，T－1均保测。特别的，若(X，B，m)是一个测度空间，T:X→X是保测映射，则称T为保测变换，此时则称(X，B，m，T)为保测系统;若T可逆，则称(X，B，m，T)为可逆保测系统。

下面是保测系统的一个基本性质，由于它在文献中很少出现及证明方法的基本性，这里将它列出。

定理1.1 若(X，B，m，T)是保测系统，则对任意f∈L1(m)，有

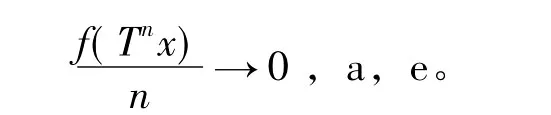
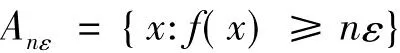
则

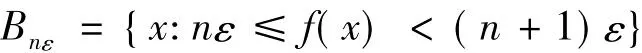
则

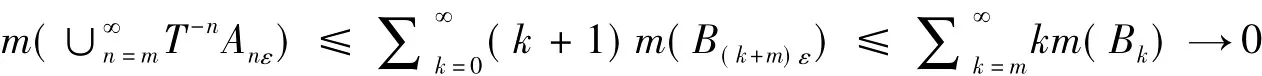
这是因为f可积。

定理［1］1.2 设(X，B，m，T)是概率保测系统，E∈B，且m(E)＞0，则E中几乎所有点在T的作用下都将无穷次的回到E中。

这是著名的庞加莱回归定理，下面给出它的一个等价命题

定理1.3 设(X，B，m，T)是概率保测系统，f:X→R是可测函数，则对于几乎处处的x∈X，有

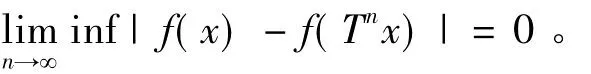
证明对任意ε＞0，将R分成可数个长为ε的互不相交的左开右闭区间的并，对于每个小区间I，f－1(I)是可测集，由定理1.2，f－1(I)中几乎所有点在T的作用下都将无穷次的回到f－1(I)中。即:

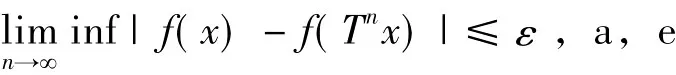
由ε的任意性知定理成立。

由定理1.3推定理1.2是容易的，所以定理1.2与定理1.3是等价的。

关于庞加莱回归定理的其它推广与应用可见文献［2］、［3］。

2 群上的Khintchine回归定理

比庞加莱回归定理更深刻的是如下的Khintchine回归定理。

定理［4］2.1 设(X，B，m，T)是概率保测系统，A∈B，ε ＞0，集合

在自然数集N当中是相对稠的，即存在有限子集F⊂N使

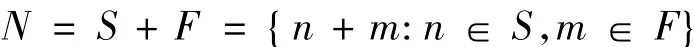
它的连续形式可见文献［5］。下面将Khintchine回归定理推广到一般的群作用上。

定义2.1 设(X，B，m)是概率测度空间，G是一个群，对每个g∈G，对应一个保测变换Tg:X→X，且满足

(1)对任意g1，g2∈G，则Tg1g2=Tg1Tg2;

(2)Te是恒等映射，其中e是G的单位元。

则{Tg:g∈G}是一个群，称为概率测度空间(X，B，m)上的保测变换群。

定义2.2 设G是一个拓扑群，A⊂G，若存在紧集K⊂G，使得G=AK，则称A左syndetic;若G=KA，则称A右syndetic;若A既左syndetic，又右syndetic，则简称Asyndetic。

关于拓扑群的内容可见文献［6］，任何一个群赋予离散拓扑便成为离散拓扑群，下面的群均指的是无限群。

若A是G的子群，则A左syndetic，A右syndetic，Asyndetic三者等价。

定义2.3 设G是一个无限群，h是整数集Z到G的映射，n∈Z在h下的像记为hn，令F是Z的有限有序子集全体，即:

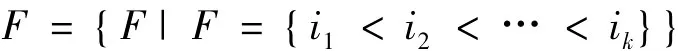
令

称π(h)为由h生成的G的IP－集。

A⊂G称为IP*－集，若A和G的所有IP－集相交。

引理［7］2.1 设Ai，i=1，2，…是概率空间(X，B，m)中的可测集，且m(Ai)=a，a是正常数，则对任意ε＞0，存在i＜j，使得m(Ai∩Aj)≥a2－ε。

引理2.2 设Ai，i=1，2，…是概率空间(X，B，m)中的可测集，且m(Ai)=a，a是正常数，则对任意ε＞0，存在无穷子列{ik}使得对任意整数p，q，有

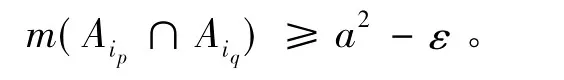
证明:先证存在某个i1，使得存在无穷序列{kj}，满足:

反证法，设这样的i1不存在，令n1=1，则存在n2＞n1，当n＞n2时有

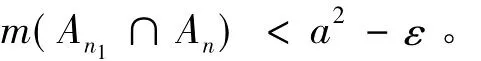
对n2，则存在n3，当n＞n3时有

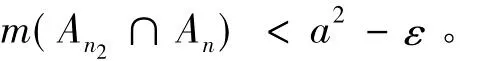
如此无限的进行下去得到序列{ni}，但是集列{Ani}不满足引理2.1，矛盾!所以，i1存在。

按照上面的做法并利用对角线法知序列{ik}存在，证完。

定理2.2 设G是一个离散拓扑群，{Tg:g∈G}是概率空间(X，B，m)上的保测变换群。则对任意A∈B，ε＞0，集合

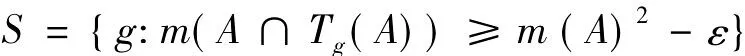
syndetic。S称为A的ε回归集。

证明:易知S是G的子群，因此若S左 syndetic，则Ssyndetic，下证S左syndetic。

设m(A)=a。

反证法，设S不左syndetic，则对G的任意有限子集K，有G≠SK。任取g1∈G令K1={g1}，必存在元素g2∈g－SK1，g∈G－S，即

令K2={g1，g2}，必存在g3∈g－SK2，且，即

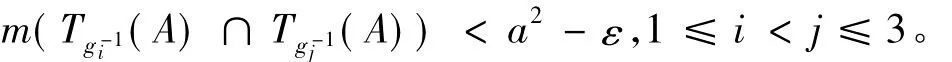
如此无限的进行下去，得到序列{gi}，它具有性质:

这与引理2.1矛盾，因此S左syndetic，所以Ssyndetic，证完。

定理2.3 设G是一个离散拓扑群，{Tg:g∈G}是概率空间(X，B，m)上的保测变换群。则对任意A∈B，ε＞0，集合

是IP*－集。

证明:设h是任意一个从整数集Z到G的映射，下证π(h)∩S≠Ø。令有限集Fi={1，2，…i}，则hFi=h1h2…hi，考虑集列{}，由引理2.1知存在i＜j，满足:

所以，hi+1hi+2…hj∈S，且hi+1hi+2…hj∈π(h)，因此π(h)∩S≠Ø，S是IP*－集。

定理2.4 设G是一个群，{Tg:g∈G}是概率空间(X，B，m)上的保测变换群。则对任意A∈B，ε＞0，存在G的无穷子集I，使得对任意g1，g2∈I，有

这是引理2.2的直接结果。

Khintchine回归定理反映了保测系统深刻的回归性质，它和系统的混合性质有密切关系，这方面的一些结果可见文献［8］。

［1］ P.Walters.An Introduction to Ergodic Theory［M］．NewYork－Berlin:Springer－Verlag，1982:26.

［2］ L.Tao，K.R.Rajaopal.A note on the applicability of recurrence theorems［J］．Commun Nonlinear Sci Numer Simulat，2009，(14):2587－2591.

［3］ M.G Nadkarni.Basic Ergodic Theory［M］．India:Hindustan Book Agency，1995:7 －9.

［4］ K.Petersen.ErgodicTheory［M］．Cambridge:Cambridge University Press，1983:37 －38.

［5］ C.visser.On poincare's recurrence theorem［J］．Bull.Amer.Math.Soc.1936，(42):397 －400.

［6］ E.Hewitt and K.A.Ross.Abstract of harmonic analysis Vol1［M］．Springer－Verlag，1963:75 －80.

［7］ V.Bergelson.Ergodic ramsey theory－an update［A］.Ergodic Theory of Zd－actions［C］．London Math.Soc.Lecture Note Series 228，1996:49.

［8］ V.Bergelson.The multifarious Poincaré recurrence theorem［A］．Descriptive Set Theory and Dynamical Systems［C］.(Marseille －Lu miny，1996)，Vol.277 of London Math.Soc.Lecture Note Series，Cambridge University Press，2000:31 －57.