块广义∂-对角占优矩阵

蒋建新

(文山学院数理系，云南文山663000)

1 预备知识

设 Cn×n(Rn×n)分别是复(实)矩阵的集合，N={1，2，…，n} ，K={1，2，…，k} 。

其中Aii为ri阶方阵，且Aii非奇异。在实际问题中Aii是稀疏的且很多是零矩阵。

定义1［1］常用的三种诱导矩阵范数:1－范数(列和范数，A的每一列元素绝对值之和的最大值)。2－范数:‖A‖2=σ1，其中σ1是A的最大奇异值，即A*A的最大特征值的非负平方根。∞ －范数(行和范数，A的每一行元素绝对值之和的最大值)。

定义2［1］设B=(bij)=(‖Aij‖)k×k不可约，则称A为块不可约，这里‖·‖是诱导矩阵范数。

定义 3［1］设则称 T(A) 为 A 的块比较矩阵。

定义4［1］若则称A为块对角占优矩阵记为A∈BD;若都是严格不等式，则称A为块严格对角占优矩阵记为A∈BSD。

定义 5［1］若存在 x=(x1，x2，…，xk)T＞ 0，使得 xi‖A－1ii‖－1＞ ∑j≠ixj‖Aij‖ ，i=1，…，k，则称 A 为块H－矩阵，记为A∈BH。

引理1［1］BSD⊂BD⊂BH。块H－矩阵包括许多子类，例如下面引理中的矩阵。

引理2［1］若A∈BD是不可约的，并且至少存在一个严格不等式(称A是块不可约对角占优矩阵)，则A是非奇异块H－矩阵。

引理3［1］若，存在一个非零元素链‖Aii1‖，‖Ai1i2‖，…，‖Airi*‖，i≠i1，i1≠i2，…，ir≠i*，i*∈J(A)，则A是非奇异块H －矩阵。

2 块广义对角占优矩阵和块H－矩阵

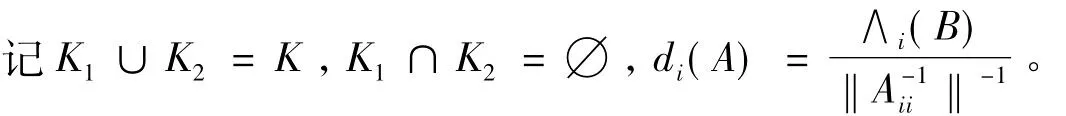
定义6 设A=(aij)∈Cn×n分块如(1)，且存在如上定义的K的子集K1，K2，若对∀∂ ∈［0，1］，当

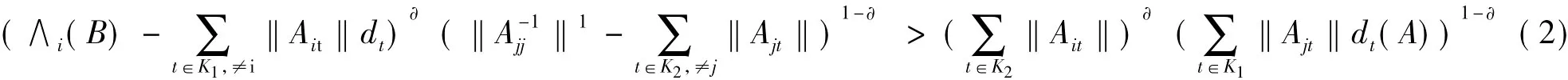
成立则称A为块广义∂—严格对角占优矩阵。

定理1 若A是块广义∂—严格对角占优矩阵，则A是非奇异块H－矩阵。时，有

证明:令

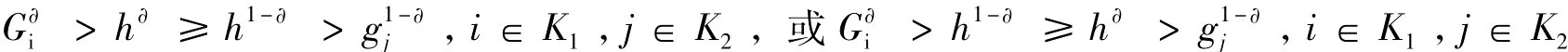
(1)当i∈K1时

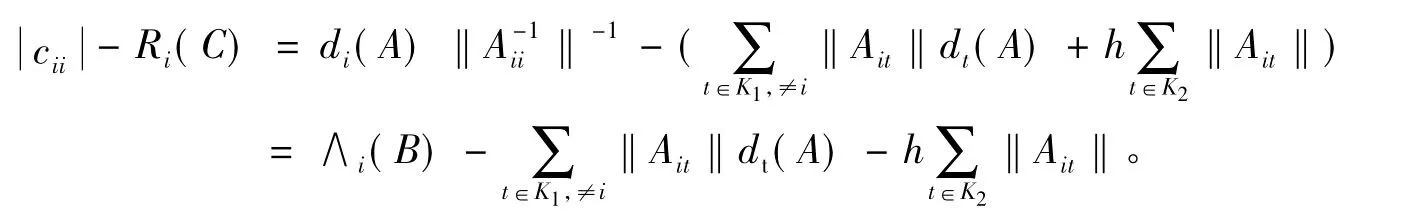
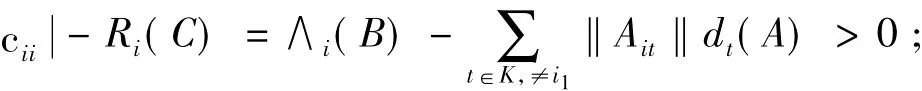
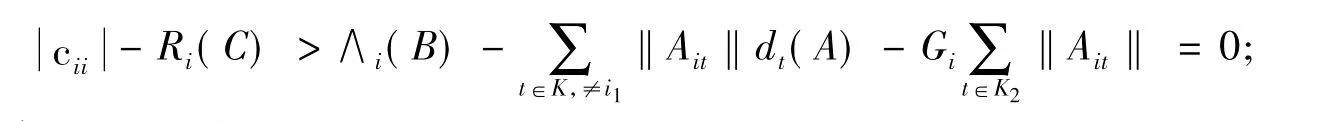
(2)当 j∈ K2时

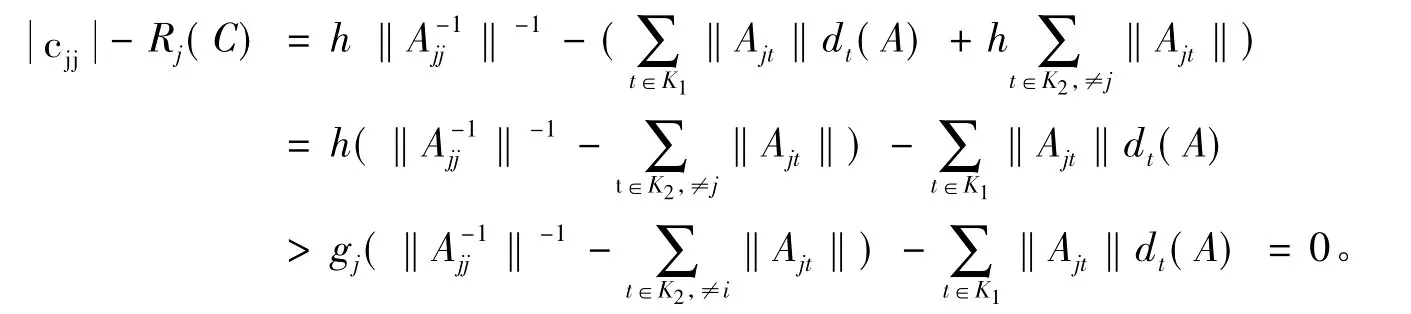
定义7 设A=(aij)∈Cn×n是形如(1)的块不可约矩阵，且存在如上定义的K的子集K1，K2，若对∀∂

综上可知时，有

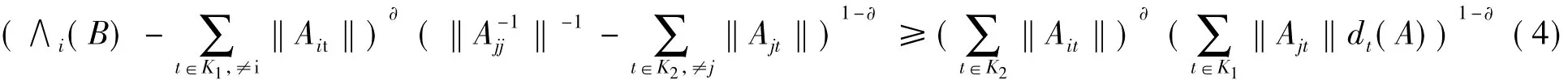
成立，且(4)式中至少有一行严格成立，则称A为不可约块广义∂—对角占优矩阵。

定理2 若A是不可约块广义∂—对角占优矩阵，则A是非奇异块H－矩阵。

证明:设Gi，gj如定理1证明中的定义，类似于定理1的证明

且在(5)式中至少存在一个严格不等式，则

因为A不可约，则存在‖Ajt‖≠0，i∈K1，j∈K2，所以l＞0。

设 X=diag(xk:xk=dk(A)，k∈ K1;xk=l，k∈ K2)

令C=T(A)X=(cij)，则

(1)当i∈K1时

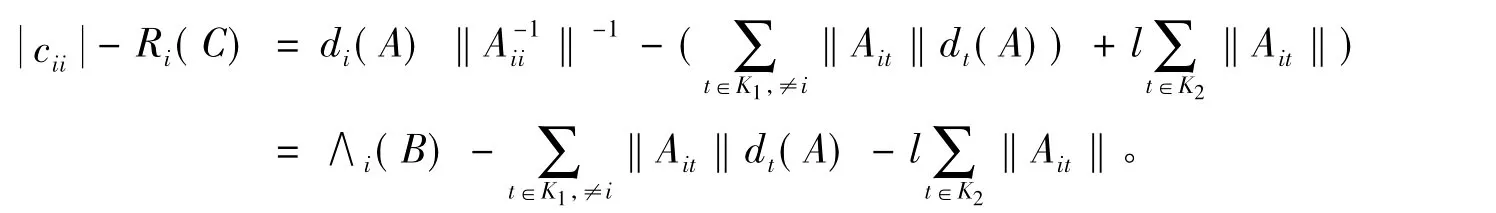
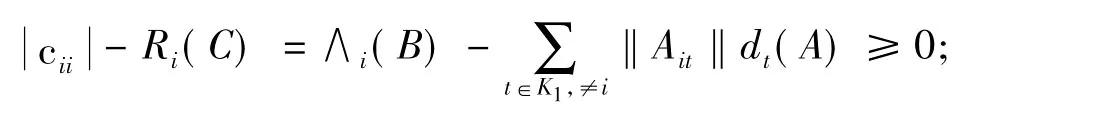
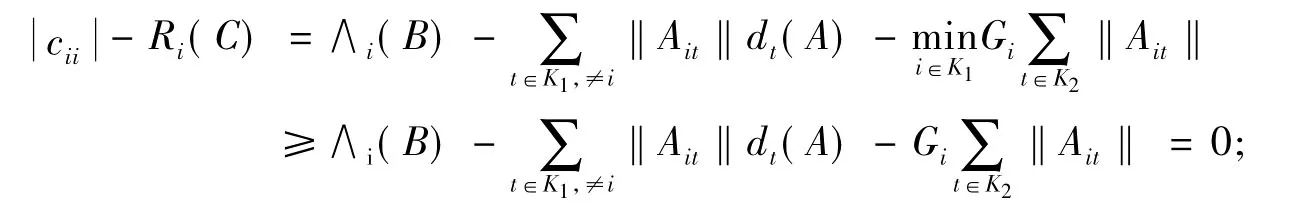
(2)当 j∈ K2时

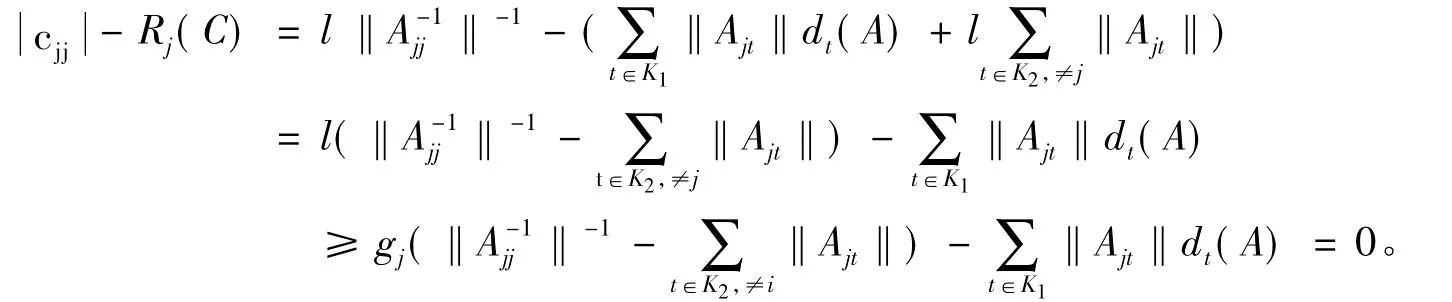
定义7 设A=(aij)∈Cn×n是形如(1)的分块，且存在如上定义的K的子集K1，K2，若对，当时，有

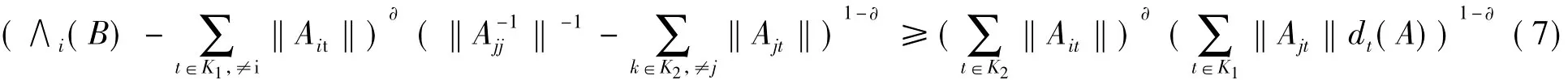
成立，且 ∀i∈ {j1，…，jk} ∪ {i1，…，il}，存在非零元素链 ‖Air1‖ ，‖Ar1r2‖ ，…，‖Ar，r*‖ ，其中 i≠ r1，r1≠r2，…r≠ i*，i*∈ (K1－ {i1，i2，…，il}) ∪ (K2－ {j1，…，jk}) ≠ Ø ，

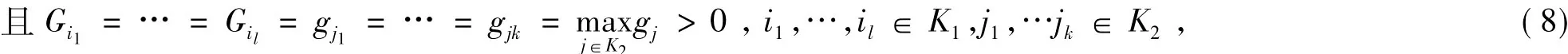
(Gi，gj的定义类似于定理1的证明中的定义)，则称A为块广义∂-非零元素链对角占优矩阵。

定理3 若A是块广义∂-非零元素链对角占优矩阵，则A是非奇异块H－矩阵。

令 X=diag(xk:xk=dk(A)，k∈ K1;xk=l，k∈ K2) ，

设C=T(A)X=(cij)，当i∈{j1，…，jk}，由(8)式和gi(i∈K2)的定义知

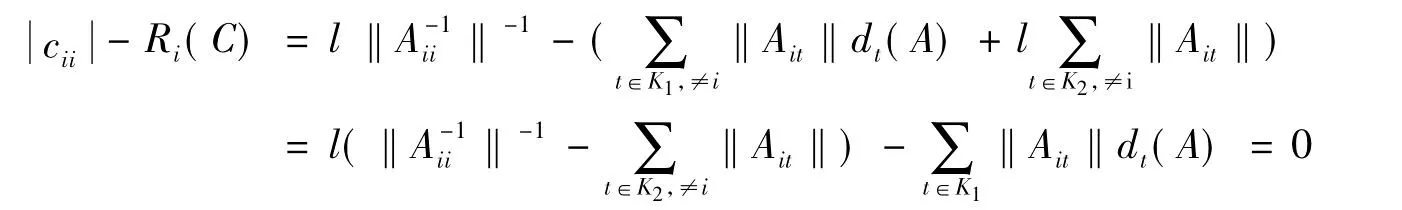
当 i∈{i1，…，il}时，由(8)式和Gi(i∈K1)的定义知

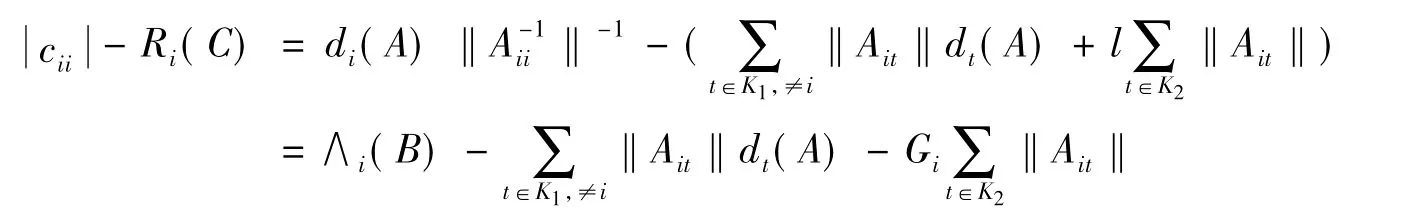
当i∈(K1－{i1，i2，…，il})∪(K2－{j1，…，jk})，相似于定理1的证明知，即C是块非零元素链对角占优矩阵，则由引理2知，C是非奇异H－矩阵，即A是非奇异块H－矩阵。

［1］ 黄庭祝，杨传胜.特殊矩阵分析及应用［M］，北京:科学出版社，2006:1－4.

［2］ Ting－zhu Huang，Chang－xian Xu.Generalized∂ －Diagonal Do minance［J］．Computers and Mathematics with Applications 45 2003:1721－1727.