气流激振力作用下转子的非线性特性研究

吴敬东， 张旭东， 鄢利群， 吴 卫， 牛 野

(沈阳化工大学机械工程学院，辽宁沈阳110142)

将(2)式化为:

随着国民经济的快速平稳发展，社会对电的需求量与日俱增，而火力发电所需要的煤炭、石油、天然气等不可再生能源储藏量又极其有限，而今我国又提倡节能减排，低碳生活.因此旋转机械正向超大型、高转速、高效率的方向发展.旋转机械的高速化、大型化渐渐暴露出一些问题.文献［1］介绍了近年来国内外发电厂一些大型机组发生的事故，最终诊断结论为气流力引发起自激振动导致系统失稳.文献［2－6］是国内外学者从不同角度对转子系统的失稳进行的研究，得出许多具有意义的结论.但实际系统的状态很复杂，引起气流激振的因素有很多方面，主要有叶顶间隙流体激振力和密封流体激振力.有必要研究在这2种激振力共同作用下转子系统的非线性运动特性，为转子系统的振动控制和故障诊断提供理论依据.

汽轮机是发电设备中一种比较普遍的大型高速旋转机械，由于其在制造和安装过程中存在偏差，导致叶片受力不均匀，使轴心发生振动现象.本文建立了汽轮机低压转子系统的动力学方程，考虑2种气流力的共同作用.并利用四阶Ruge-Kutta法对其进行数值模拟研究，对系统的非线性特性进行分析.

1 系统的力学模型及系统方程

以200 MW汽轮机低压转子为研究对象，其结构［7］如图1所示.图1中三角形处为轴承支持，结构简图如图2所示，受力图如图3所示.其中fax、fay为叶顶间隙激振力Fa在x和y向的分力.

图1 200 MW汽轮机低压转子结构简图Fig.1 200 MW low-pressure steam turbine rotor stracture diagram

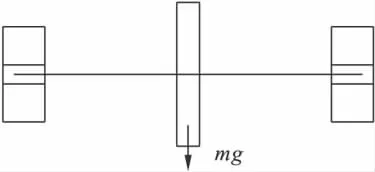
图2 系统简化结构图Fig.2 Simplified structure diagram of the system

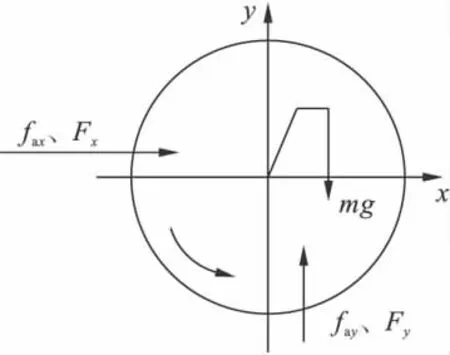
图3 系统受力图Fig.3 Loading diagram of the system

将机组低压转子的轴系简化成刚性圆盘，用功的互等定理将密封力Fx、Fy等效的作用在圆盘上，建立系统的动力学方程:

其中:Fa为叶顶间隙激振力，m为圆盘质量，De为转子外阻尼系数，Ke为轴的刚度，圆盘转动角速度为ω，x、y为圆盘的轴心位移，Fx，Fy为密封流体激振力.

由于200 MW汽轮机低压转子是扭叶片，叶顶间隙激振力采用文献［6，8］中的扭叶片激振力计算公式:

其中:

β10为叶根部进气角，β11为叶尖部进气角，β20为叶根部出气角，β21为叶尖部出气角，h为叶高，ρ0为气流密度，RT为叶尖半径，RB为叶根半径，φ为速度系数，v1为进气速度，δ为平均间隙.

密封力采用Muszynska模型［4，9］，其表达式为:

其中:

密封特性系数K0，D0，mf采用Childs的短密封轴承解析公式:

Δp是密封压降，z是进口损失系数，l是密封长度，δ是径向密封间隙，v是轴向流速，R是密封半径，Ra是轴向流动雷诺系数，Rv是周向流动雷诺系数，λ是摩擦因子，σ是摩擦损失梯度系数，n0，m0用于描述具体的密封参数.

对系统方程(1)进行无量纲变换有

将(2)式化为:

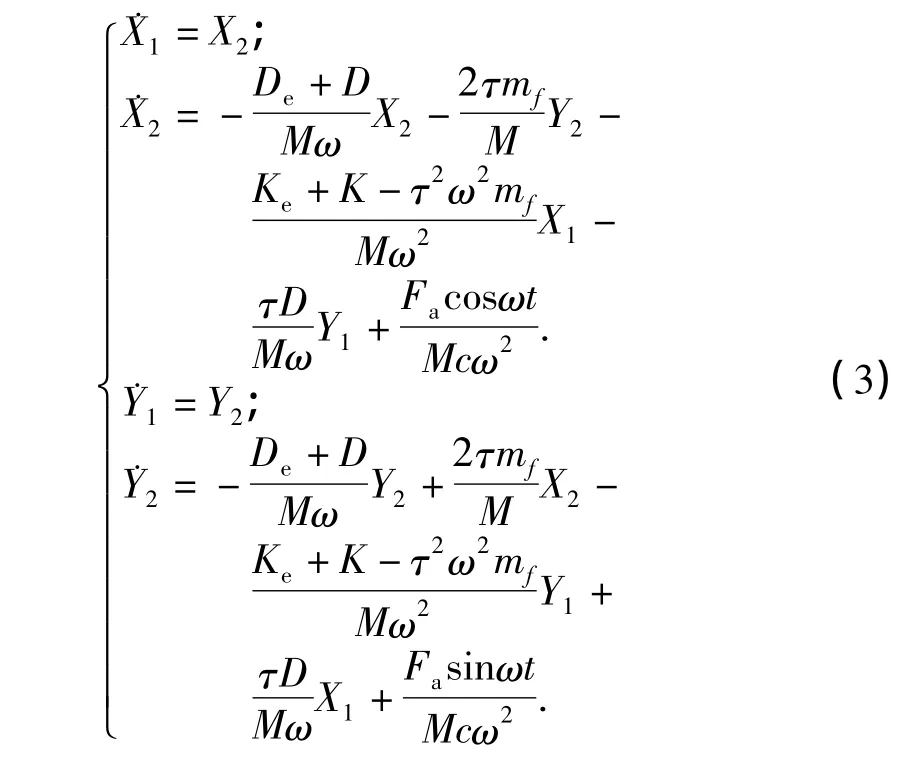
2 数值仿真和计算结果分析

在方程(3)中，由于K、D、τ都是位移的函数，系统是一个典型的非线性系统，故无法用常规的方法求出理论解，再加上气流激振力的影响，使系统变得更加复杂.这里采用四阶Ruge-Kutta法对上述系统进行数值仿真，给出有气流激振时转子-轴承系统响应的分岔图、轨迹图以及Poincare映射图.

系统参数为:m=50 kg，Ke=7.276 2×106N·m－1，De=2 000 N·s·m－1，φ=0.83，e=0.2 mm，l=0.102 m，z=0.1，n=2.5，b=0.45，τ0=0.4，c= 0.33 mm，m0=－0.25，n0=0.079，v=50 m·s－1，δ= 0.30 mm，R=0.067 m，ρ0=11.8 kg/m3，RT=0.5 m，RB=0.37 m，β10=35°，β11=25°，β20=40°，β21=45°，ζ=0.84，δ0=1.2×10－2m，v1=30 m·s－1.

图4和图5分别为水平方向和垂直方向无量纲振动随转速变化的分岔图，从图4和图5可以得知，转子系统在2种气流激振力的共同作用下，呈非线性运动状态.水平和垂直方向的振动随转速由一周期经过二分岔-四分岔进入混沌状态，在小于400 r/min时为1周期运动，在小于400～720 r/min时为2周期运动，在720～750 r/min时为4周期运动，在780 r/min时为周期运动，在820 r/ min时为6周期运动，之后进入混沌状态.随转速的不断增加，转子系统在1 800 r/min时进入1周期运动状态.此时系统的最大Lyapunov指数图如图6所示，从图6可看出系统存在3个明显的混沌区域，且在第2和3区域有明显的一个较宽周期窗口.图7～图14为转子在不同转速ω下的轴心轨迹和无量纲轴心轨迹Poincare映射图.

图4 水平方向转子振动分岔图Fig.4 Bifurcation diagram of X

图5 垂直方向转子振动分岔图Fig.5 Bifurcation diagram of Y

图6 转子的最大Lyapunov指数图Fig.6 The maximal Lyapunov expoent map

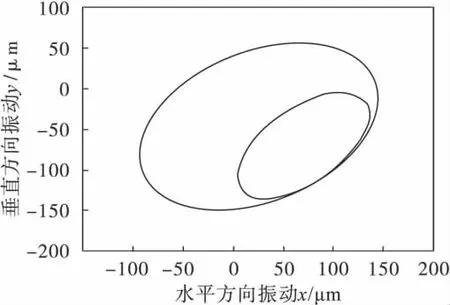
图7 转子在600 r/min时的轴心轨迹图Fig.7 Axial trace of rot or at 600 r/min

图8 转子在600 r/min时的Poincare映射图Fig.8 Poincare map at ω=600r/min

图9 转子在730 r/min时的轴心轨迹图Fig.9 Axial trace of rot or at 730 r/min

图10 转子在730 r/min时的Poincare映射图Fig.10 Poincare map at ω=730 r/min

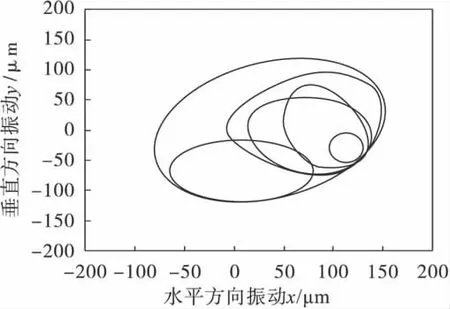
图11 转子在820 r/min时的轴心轨迹图Fig.11 Axial trace of rot or at 820 r/min

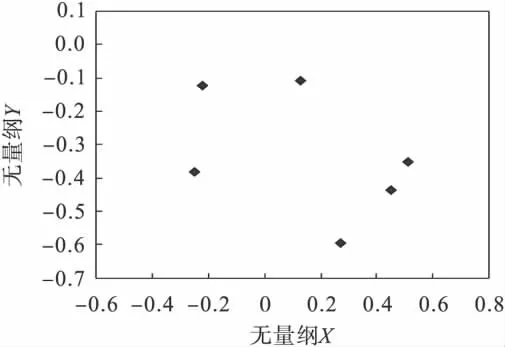
图12 转子在820 r/min时的Poincare映射图Fig.12 Poincare map at ω=820 r/min

图13 转子在1 800 r/min时的轴心轨迹图Fig.13 Axial trace of rot or at 1 800 r/min

图14 转子在1 800 r/min时的Poincare映射图Fig.14 Poincare map at ω=1 800 r/min

图15为转子径向密封间隙δ在0.05～0.30时的振动分岔图，由图15可看出:当径向密封间隙δ在0.05～0.17时系统处于比较稳定状态;当径向密封间隙δ大于0.17时，系统经历了一段混沌状态，进入概周期状态，最后完全进入混沌状态.图16为对应的最大Lyapunov指数图，其结论与图15相一致.图17～图24为转子随径向密封间隙δ变化的轴心轨迹图和无量纲轴心轨迹Poincare映射图.在δ=0.1时，转子呈现1周期运动状态，在δ=0.15时，为2周期运动状态，在δ= 0.20时，转子系统进入概周期运动状态，在δ= 0.21时，转子系统进入混沌运动状态.

图15 水平方向转子振动分岔图Fig.15 Bifurcation diagram of X

图16 转子的最大Lyapunov指数图Fig.16 The maximal Lyapunov expoent map

图17 转子在δ=0.1时的轴心轨迹图Fig.17 Axial trace of rot or at δ=0.1

图18 转子在δ=0.1时的Poincare映射图Fig.18 Poincare map at δ=0.1

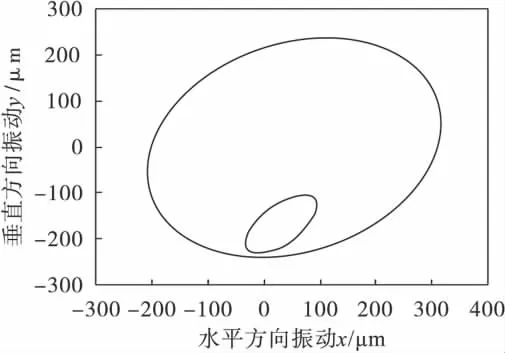
图19 转子在δ=0.15时的轴心轨迹图Fig.19 Axial trace of rot or at δ=0.15

图20 转子在δ=0.15时的Poincare映射图Fig.20 Poincare map at δ=0.15

图21 转子在δ=0.20时的轴心轨迹图Fig.21 Axial trace of rot or at=0.20

图22 转子在δ=0.20时的Poincare映射图Fig.22 Poincare map at δ=0.20

图23 转子在δ=0.25时的轴心轨迹图Fig.23 Axial trace of rot or at δ=0.25

图24 转子在δ=0.25时的Poincare映射图Fig.24 Poincare map at δ=0.25

3 结论

以200 MW汽轮机低压转子为研究对象，对转子在叶顶间隙气流激振力和密封流体激振力共同作用下的非线性特性进行了分析，得到如下结论:

(1)建立了叶顶间隙激振力和密封流体激振力共同作用下转子系统的动力学方程，并运用数值分析方法进行了仿真研究;

(2)转子水平方向和垂直方向的振动特性是同步的，即水平方向和垂直方向的振动从周期运动进入混沌的转速基本相同;

(3)密封间隙系数δ对系统的动态响应有较大影响.密封间隙系数δ的减小可以减少和抑制混沌运动的发生.

［1］ 韩红林.200 MW汽轮发电机组汽流激振分析与治理研究［D］.北京:华北电力大学，2005:1－6.

［2］ Zhang W，Zhang H S，Xu X F.Study of General Nonlinear Formula of Oil-film Force Acting on a Journal with Unsteady Motion［J］.Asia-Pacific Vibration Conferences，Korea，1997，37(3):824－829.

［3］ 李永.转子-轴承-密封系统的非线性振动与分岔［D］.大连:大连理工大学，2007:8－9.

［4］ 李松涛，许庆余，万方义.迷宫密封转子系统非线性动力稳定性的研究［J］.应用力学学报，2002，19 (2):27－30.

［5］ 柴山，张耀明，曲庆文，等.汽轮机间隙气流激振力分析［J］.中国工程科学，2001，3(4):68－72.

［6］ 柴山，张耀明，赵又群，等.汽轮机非线性间隙气流激振力分析(Ⅰ)—相对进气速度沿叶高不变［J］.非线性动力学报，2000，7(2):25－32.

［7］ 孟泉，陈予恕.非线性转子-轴承系统油膜失稳新机理研究［J］.非线性动力学学报，1995，2(3):189－197.

［8］ 辛晓辉，曹树谦，丁千.汽轮机转子在气流力和油膜力作用下的非线性动力学特性［J］.非线性动力学学报，2005，12(1):45－52.

［9］ Bently D E，Muszynska A.Role of Circumferential Flow in the Stability of Fluid-handling Machine Rotors［C］//The 5thWorkshop on Rotordynamics Instability Problems in High Performances Turbomachinery.Taxas:Taxas A＆M Univercity，1988:1－5.