通过误差分析确定实验方案的可行性
2011-01-25叶晓
叶晓
(余杭高级中学 浙江 杭州 311100)
2011年浙江省普通高考考试说明,对误差知识的要求是:认识误差问题在实验中的重要性,了解误差的概念,知道系统误差和偶然误差,能在某些实验中分析误差的主要来源;不要求计算误差.而作为一名合格的教师,不但要求熟练掌握规范的实验操作,还应该能正确运用误差理论分析实验方案的可行性.现以一道模拟题为例.
【题目】某实验小组要测量一节干电池的电动势和内电阻,实验室提供的实验材料如下
A.待测的干电池(电动势约为1.5 V,内电阻约为2 Ω)
B.电压表V1(0~3 V,内阻Rv1=4 000 Ω)
C.电压表V2(0~3 V,内阻Rv1约为3 500 Ω)
D.电流表A(0~3 A,内阻0.1 Ω)
E.电阻箱R1(0~9 999 Ω)
F.滑动变阻器R2(0~200 Ω,1 A)
G.开关和导线若干
(1) 该小组根据以上实验器材设计了如图1所示的电路,并进行以下的实验操作.

图1
1)闭合开关S1和S2,记下此时V1○的读数U1;

请你根据以上实验记录的物理量和已知的物理量写出该干电池的电动势和内电阻的表达式:E=______,r=______.
(2)在现有器材的条件下,请你选择合适的实验器材,再设计出一种测量干电池电动势和内电阻的方案,并在右边虚线中画出实验电路图.

解析:对第(1)小题,从理论上可以计算出
容易产生这样的疑问:电压表的内阻有4 000 Ω和3 500 Ω,能测出只有约2 Ω的电源内阻吗?
为了回答这个问题,笔者对这个方案做误差分析.观察者在读取数据时难免会有误差,例如量程0~3 V的电压表,假设刻度盘上每一小格为0.1 V,能估读到0.01 V,估读产生的不确定性至少有0.01 V.
对图1,当S1,S2闭合,V1的读数为U1,有
故

由误差理论得
其中RV1远大于r,则U1≈E,代入数据得
由于电压表的读数不准引起电阻测量误差大于26.7 Ω.而干电池的内阻只有2 Ω左右,这就意味着该方案不可能测量出干电池的内阻.
对第(2)小题,容易设计出图2两种方案.那么这两种方案是否实际可行?也对它们进行误差分析.图2(a)方案的误差分析如下.
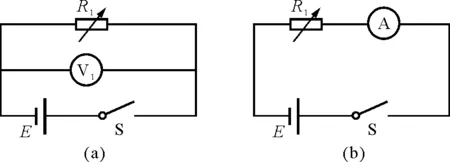
图2
根据闭合电路欧姆定律得

(1)
故
根据误差理论得
(2)
由(1)式和(2)式得到

通过以上定量的计算发现,测量电动势内阻的最小相对误差是2.65% .该方案可以较准确地完成实验.
再对图2(b)方案做误差分析.根据闭合电路欧姆定律得
E=I(R1+rA1+r)
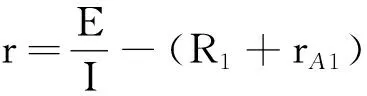
根据误差理论得
(3)
由(3)式可知电流表的读数越大,测量误差越小.当电阻箱的电阻调节到零,电流最大值约为0.71 A,则最小误差为
通过以上定量的计算发现,测量电动势内阻的最小相对误差是1.49%,比图2(a)的方案还要精确.当然,如果题目中电流表的量程为0~0.6 A,则实验结果会更加精确.

由此可见,在实验教学中,教师不能只凭着经验和感觉分析实验方案的可行性,而应通过误差分析确定实验方案的可行性.
