例析Matlab融入电磁学教学课堂*①
2011-01-25吕良军郝振莉
吕良军 郝振莉
(黄河水利职业技术学院 河南 开封 475004)
郑海务 尹国盛
(河南大学物理与电子学院 河南 开封 475004)
1 引言
目前,在我国许多大学、中小学都已普及了以电子教案为基体、计算机为主体的多媒体教学.教师们大量地采用自编的或公开出版的电子教案教学,与传统的“粉笔黑板”式的教学相比,有多方面的优越性,但多以Powerpoint为主,而物理学中的许多最终结果和运动难以用Powerpoint软件完成.鉴于上面的原因,物理仿真已引起了大家的普遍关注与研究[1~4].
电磁学历来被国内外大学生公认为大学物理中难度较大的课程之一,其较深的数学理论和场的抽象性使得学生在学习中往往有恐惧心理,容易产生畏难情绪.如果按照传统的课堂教学方式,必然会面对大量复杂繁琐的数学推导和难以绘制的三维图形,很难引起学生的学习兴趣.Matlab是近些年来较为流行的一种可视化科学计算软件,其计算与画图功能强大,编程简单,将其引入电磁场的课堂教学中,可以把抽象的场可视化,让教师和学生从繁琐的数学推导运算中解放出来,将更多的精力放到对概念的理解和专业知识的获取上.本文通过几个典型例子介绍如何利用Matlab进行电磁学的辅助分析及可视化教学.
2 典型案例
2.1 带电粒子在电磁场中的运动仿真
既有电场又有磁场的情况下,运动的带电粒子q在此区域内所受到的作用力应为
F=FE+FM=qE+qυ×B
上式通常被称为洛伦兹力公式.因此,可以利用外加的电场和磁场,来控制带电粒子流的运动[5].在Matlab中只要采用不同的初始条件和参量就可以观察到不同的现象.下面程序是q=1.6×10-2、m=0.02的带电粒子在B=2、E=1的均匀电磁场中的运动仿真程序和运动轨迹.
clc;clear;[t,y]=ode45(′ode45_fun4′,[0:0.1:20],[0 0.01 0 6 0 0.01]);
plot3(y(:,1),y(:,3),y(:,5),′linewidth′,2); %画运动轨迹
grid on;hold on;n=length(y);
for k=1:n
h=plot3(y(k,1),y(k,3),y(k,5),′.′);
set(h,′color′,[1 0 0],′markersize′,28); %定义带电粒子的颜色与大小
M(k)=getframe; %获取单帧
end
movie(M,1) %播放动画
程序运行完毕,效果如图1所示.
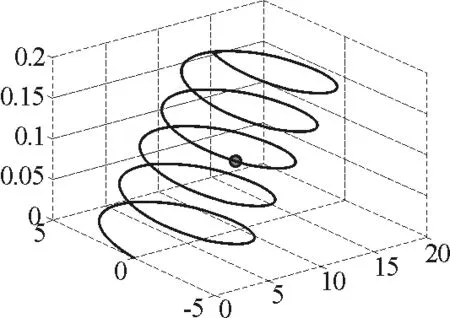
图1 带电粒子在电磁场中的运动轨迹
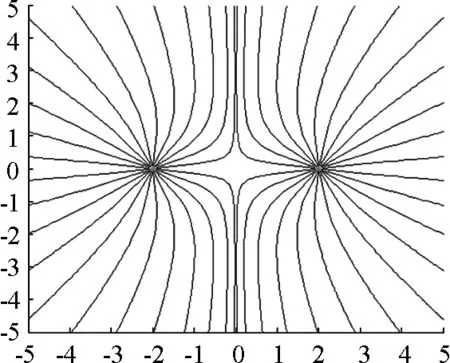
2.2 电偶极子电场和等势线的分布图绘制
在电磁理论中,电偶极子是指由间距远比场点到它们的距离小得多的两个等量异号电荷组成的系统, 其等位线和电场线的绘制就是课程中较难把握的内容[5].其模型是指电荷量为q、相距为l的一对正负点电荷所组成,O是两个点电荷距离的中点,如图2所示.在直角坐标系中,取偶极子中心作为坐标原点,远处一点P的电势等于两点电荷电势的叠加.

图2 电偶极子P点电场
在二维直角坐标系中,设在(a,b)处有电荷+q,在(-a,b)处有电荷-q,那么在电荷所在平面上任何一点P(x,y)的电势为[2]
其中
电场为
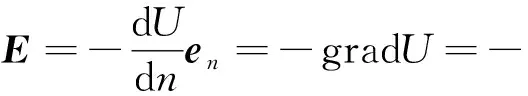
设电荷电量q=1,a=1,b=0.在Matlab编程如下:
[x,y]=meshgrid(-2:0.1:2,-2:0.1:2);
[px,py]=gradient(z); %求电势在x,y方向的梯度即电场强度
contour(x,y,z,[-12:0.5:12]);hold on;
quiver(x,y,px,py,′k′)
运行后可见电偶极子的等势线及电场线在二维平面上的分布,如图3所示.
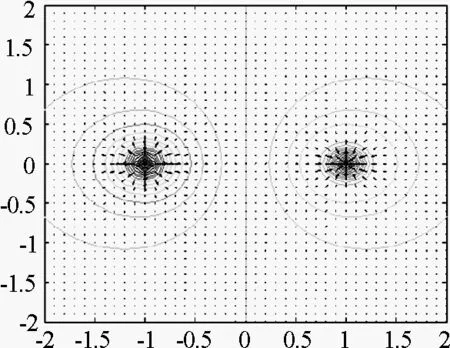
图3 电偶极子平面等势线及电场线
通过将抽象的场函数仿真后,对场的分布就有了一个直观的概念,对场的性质理解起来也就更加容易.电场线的疏密表示电场的弱强,某点处切线方向表示电场的方向,从而建立起电场线与电场强度之间的有效联系.而且等势线与电场线正交,顺着电场线方向电势降低,电场强度是电势的负梯度等,这些从图像中都可以得到直接验证.
调整a的值,可以仿真电偶极子的电势三维空间分布:
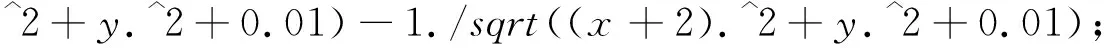
mesh(x,y,z);%画三维网格图
效果如图4所示.
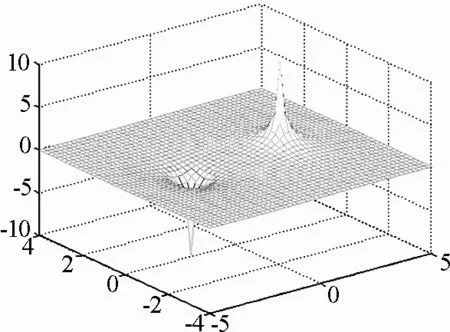
图4 电偶极子的电势三维空间分布
2.3 求解电磁学中微积分问题
均匀带电球面的电场中电势的分布[5],设球面的半径为R、总电荷量为q.
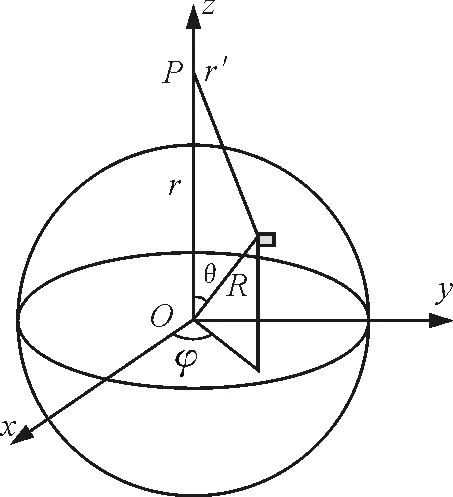
图5 均匀带电球面的电场中电势
整个球面在P点产生的电势为
根据图5,由余弦定理得
代入上面UP式得
上式的积分可用Matlab求解,程序如下:
%利用Matlab求解积分问题
clear; syms sigma theta epsilon vartheta
R r %定义符号变量
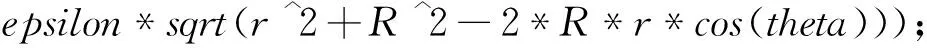
Up=int( int(fx, theta,′0′,′pi′),
vartheta,′0′,′2*pi′) %对函数求两次积分
运行程序,得
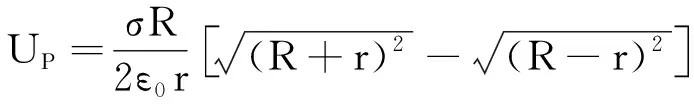
当P点在球外,即r>R时,有
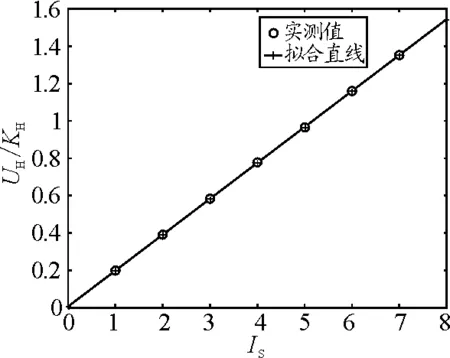
当P点在球内,即r 在20世纪50年代前,计算电磁场问题主要依靠解析法及经验公式.然而用解析法求得的解析解并不能完全满足实际应用中的要求,有些问题是难以求得解析解的.因而用数值法求解电磁场问题就越来越具有优越性.利用Matlab软件可以给出符合需要的结果和相关图像,为电磁场理论教学和工程实际起到积极作用.例如等量同号电荷的电场线的绘制. 由电场中任一点的电场方向都沿该点电场线的切线方向,所以满足 引入参变量t得到 设二点电荷位于(-2,0)和(2,0),二电荷电量为q1和q2(数值计算时q=10),得微分方程 用Matlab数值计算解此方程就绘制出电场线(图6).程序如下: Clc;Clear;q1=10;q2=10;axis([-5 5 -5 5]);hold on;plot(2,0,′*r′);plot(-2,0,′*r′) a=(pi/24):pi/12:(2*pi-pi/24); b=0.1*cos(a);c=0.1*sin(a); b1=-2+b;b2=2+b;b0=[b1 b2]; c0=[c,c]; for i=1:48 [t,y]=ode45(′ode45_fun3′,[0:0.05:40],[b0(i),c0(i)],[],q1,q2); %微分方程数值解 plot(y(:,1),y(:,2),′b′) %画电场线 end 程序运行完毕,效果如图6所示. 图6 等量同号电荷的电场线 在霍尔效应测磁场的实验中,为测某一磁场的磁感应强度,测得的实验数据[6]如表1. 表1 霍尔效应测磁场实验数据 Is/mA5.00 6.00 7.00 UH/mV12.897 515.480 018.067 5 clear;IS=1:7;UH=[2.592 5 5.157 5 7.742 5 10.330 0 12.897 5 15.480 0 18.067 5]; KH=13.380 0;UK=UH/KH;n=length(IS); xjz=mean(IS);yjz=mean(UK); Lxx=sum(IS.*IS)-1/n*sum(IS)*sum(IS); Lyy=sum(UK.*UK)-1/n*sum(UK)*sum(UK); Lxy=sum(IS.*UK)-1/n*sum(IS)*sum(UK); b=Lxy/Lxx;a=yjz-b*xjz;ISS=0:8;UKK= a+b*ISS;plot(IS,UK,′O′,ISS,UKK,′-r+′); xlabel(′I_S′);ylabel(′U_H/K_H′);legend(′实测值′,′拟合直线′);b,a 注:这里也可以用Matlab自带函数polyfit直接拟合,命令为polyfit(IS,UK,1). 图7 霍尔效应直线 运行结果:b =0.192 8,a =4.537 7×10-4,即拟合直线如图7所示.方程为 磁感应强度为 B=0.192 8 T 利用Matlab进行电磁场计算及可视化教学,简化了繁琐的数学推导,将抽象的概念具体化.经课堂使用后发现该方法受到学生欢迎,并改善了教学效果.在此基础上,进一步研究电磁场仿真实验教学,鼓励学生自己动手用Matlab解决电磁场问题,特别是应用偏微分方程工具箱在大学物理电磁学等各类物理场的数值仿真. 将Matlab融入到电磁场的教学中,介绍给学生用计算机计算和仿真来学习和解决电磁问题的方法,从而培养他们采用多种途径、多个方法解决问题的能力,这正符合了以提高学生综合素质为目的的教改需要. 参考文献 1 谢处方,等.电磁场与电磁波.北京: 高等教育出版社,2002 2 彭芳麟.数学物理方程的MATLAB解法可视化.北京:清华大学出版社,2004 3 钟季康,等.大学物理习题计算机解法——MATLAB编程应用.北京:机械工业出版社,2008 4 何红雨.电磁场数值计算法与Matlab实现.武汉:华中理工大学出版社.2005 5 尹国盛,等.大学物理.北京:机械工业出版社,2010 6 王世芳,吴涛.Matlab在电磁学实验教学中的应用.湖北第二师范学院学报,2008(2)2.4 数值方法及实现电磁场数值计算融入教学
2.5 处理电磁学中的实验数据


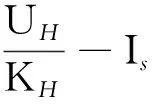
3 结束语
