电磁场矢势和标势从洛伦兹势变换到库仑势的证明*①
2011-01-25李伙全武斌
李伙全 武斌
(扬州大学物理科学与技术学院 江苏 扬州 225002)
在近代物理学中,规范变换是作为基本方法而引入的.规范不变性是一种重要的物理原则,电磁场的标势φ与矢势A满足规范变换与规范不变性.在处理时变电磁场问题时,常采用库仑规范与洛伦兹规范.在求解电磁场方程时,采用库仑规范得出的解(A库,φ库)称为库仑势;在采用洛伦兹规范时得出的解(A洛,φ洛)称为洛伦兹势.为了使学生比较容易地理解标势φ与矢势A的规范变换与规范不变性,本文证明了洛伦兹势经过一个规范变换成为库仑势.
1 电磁场中标势φ与矢势A的规范变换及规范不变性回顾
在一般情况下,真空中的电磁场所满足的规律由麦克斯韦方程组[1]

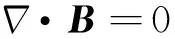
给出,其中,D=ε0E,B=μ0H,ρ表示体电荷密度,J表示体电流密度,E表示电场强度,H表示磁场强度,B表示磁感应强度,D表示电位移矢量.

因此可引入标势φ,使得
从而求出


则可得
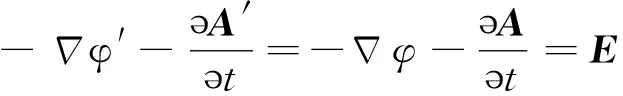
即(A′,φ′ )与(A,φ)描述同一电磁场.这样的变换称为势的规范变换,每一组(A,φ)称为一种规范.由矢势A和标势φ所表示的电磁场E和B,当其矢势A和标势φ作规范变换时,E和B都保持不变,且A和φ所满足的势方程也是不变的,称这种不变性为电磁场的规范不变性.从数学上说,规范变换自由度的存在,是由于势的定义式中,只确定A的旋度,而没有确定A的散度.在实际应用中,常用库仑规范和洛伦兹规范.
2 在库仑规范与洛伦兹规范下势满足的微分方程及其解库仑势与洛伦兹势
由麦克斯韦方程组可以推导出矢势A和标势φ所满足的基本方程[2]如下
这是适用于一般规范的方程组.
以下给出在库仑规范与洛伦兹规范下势满足的微分方程及其解,以及库仑势与洛伦兹势.
在洛伦兹规范下,势方程为[2]
(1)
(2)
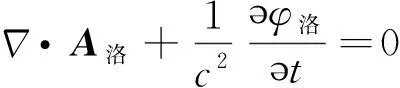
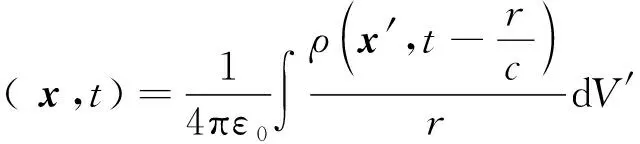
(3)
其中,x′是电荷分布点,x是观察点,r是x′到x的距离,下同.
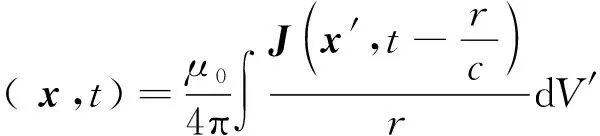
(4)
其中,x′是电流分布点,x是观察点,r是x′到x的距离,下同.
在库仑规范下,势方程为[2]
(5)
(6)
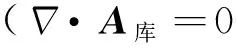
方程(5)的解为瞬时库仑势[2]
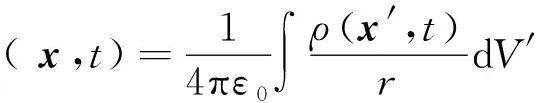
(7)
方程(6)的解是推迟势A洛(x,t)的横向分量[3]
A库(x,t)=A洛(x,t) =
(8)
我们把洛伦兹规范下,势方程之解式(3)与(4)叫洛伦兹势;库仑规范下,势方程之解式(7)与(8)叫库仑势.
3 洛伦兹势与库仑势的关系洛伦兹势经过一个规范变换成为库仑势
以下证明,洛伦兹势经规范变换为库仑势.

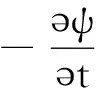
若要A库与φ库满足库仑规范条件,即
(9)
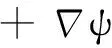
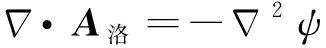
(10)
下面证明经过上述规范变换,洛伦兹势(A洛,φ洛)变成库仑势(A库,φ库).即要证明(A库,φ库)满足库仑规范下的势方程.
首先证明A库满足库仑规范下的势方程.


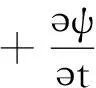

即
(11)
而A洛与φ洛满足洛伦兹规范条件,将
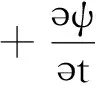
即
(12)
将(10)式代入(12)式得
(13)
将(13)式两边取梯度得
(14)
即
(15)
将(15)式代入(11)式得
这正是库仑规范下的矢势A所满足的方程.
其次证明φ库满足库仑规范下的势方程.
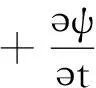
即
(16)
而洛伦兹规范条件为
该式对时间t求导,得
从而可得
而

从而可得
即
而
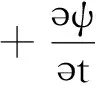
从而可得
即

(17)
将(17)式代入(16)式得
这正是库仑规范下所满足的势方程.
4 结语
本文以麦克斯韦方程组及库仑规范与洛伦兹规范下电磁场的矢势A和标势φ所满足的微分方程为基础,将洛伦兹势φ洛和A洛,经过一个规范变换后,变为库仑势φ库和A库,并将此作为电磁场的规范不变性的一个例子引入到教学环节中,从而加强学生对势的规范变换与规范不变性的理解.
参考文献
1 刘迎春,王秀江.电动力学.长春:吉林大学出版社,2006
2 郭硕鸿.电动力学(第三版).北京:高等教育出版社,2008
3 郭亮.电磁场中矢势A的特性研究.喀什师范学院学报,2007,28(6)
