点波源干涉图样的数学形式是双曲线

陈玉奇

(姜堰中等专业学校 江苏 泰州 225500)

1 双曲线的定义

在高中数学《解析几何》中，到两定点的距离之差为一定值的动点所构成的圆锥曲线就是双曲线,如图1所示.点波源形成的干涉图样是多组双曲线.

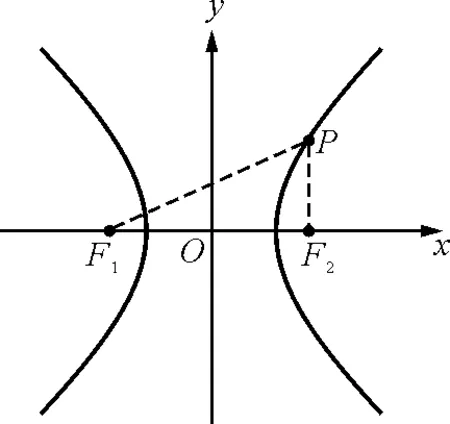
图1

2 波的干涉图样

如图2所示，如果两个点波源S1，S2是相干波源，则它们形成的两列波在空间相遇，形成稳定的叠加，即干涉.干涉图样在空间形成对称图形[1]，从中间到两边依次是中央加强区,1级减弱区,1级加强区,2级减弱区,2级加强区……加强区由振动总是加强的点构成，减弱区由振动总是减弱的点构成.

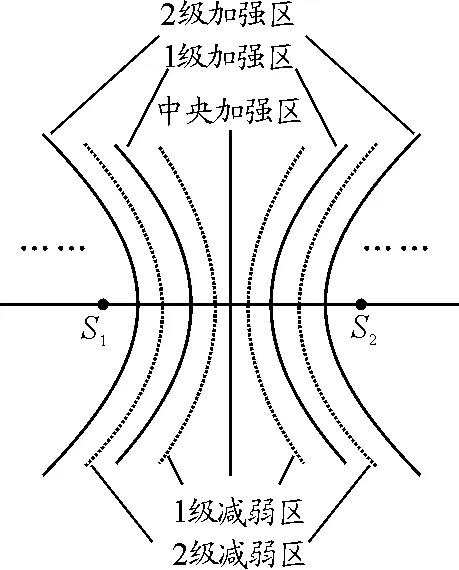
图2

如果空间任一点到两相干波源的波程差Δx满足以下关系，则该点就在相应的加强区或减弱区上.

中央加强区 Δx=0

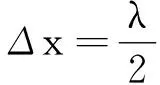
1级加强区 Δx=λ

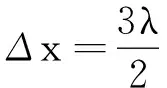
2级加强区 Δx=2λ

……

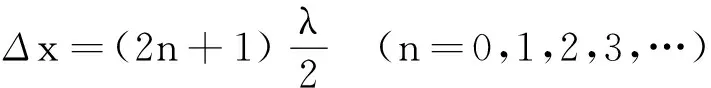
n级加强区 Δx=nλ(n=0，1，2，3，…)

可见，加强区与加强区总是相互间隔分布，在空间的位置确定，空间任一点的性质是永远不变的.加强区上点的振幅为两列波振幅之和(A1+A2)，大起大落；减弱区上的点的振幅为两列波振幅之差(│A1—A2│)，小起小落.因为每一个点都在不停地振动，所以干涉图样是动态变化的.

3 双曲线与波的干涉图样

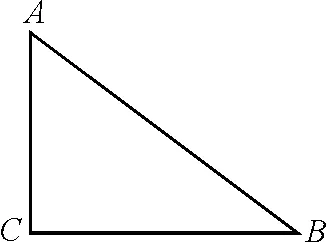
图3

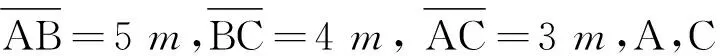
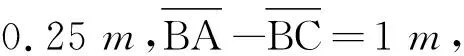
点评:点波源干涉图样的数学形式是双曲线.认清本质，持其两端，跨越过程，寻找交点，是解决此类问题的方法.

图4

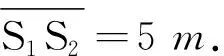
A.1处 B.3处

C.5处 D.无数处

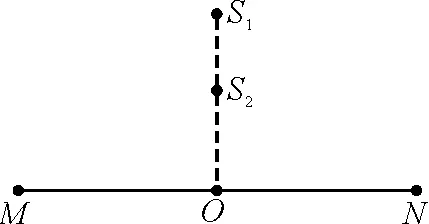
图5

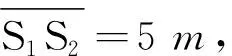
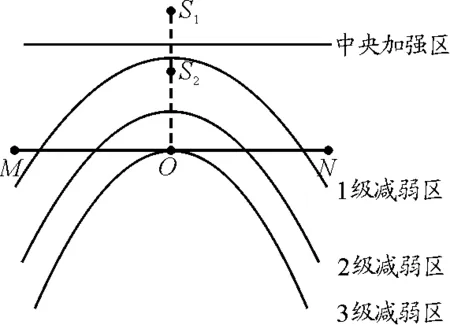
图6

点评:破解该题的思路至关重要,岸边始终平静的地方即干涉减弱点；湖岸与减弱区的交点的个数，也就是形成减弱区的双曲线的条数.

参考文献

1 漆安慎，杜婵英.力学基础.北京：高等教育出版社，1993