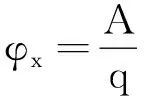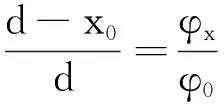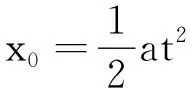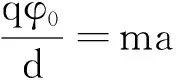构建模型巧解2011年高考物理压卷题

2011-01-25叶广新

物理通报 2011年12期

叶广新

(广西昭平中学广西贺州 546800 )

在2011年全国各地高考物理试卷中，最受瞩目的是北京卷.许多考生用“难”字来评价试题的特点及考后感受.2011年北京卷理综物理部分试题到底为什么让人觉得如此之难？究竟难在什么地方？北京地区某高考研究中心的教师们在高考结束第一时间解读该题后得出结论：所谓的“难”题，其实是“怪”题或“部分超纲”题.在物理压卷题中，其语言模式和竞赛相近，用“A”来描述能量，又加之考查较为生僻的“电势”，多数考生极不适应.

笔者还注意到，在高考答案公布之前，北京地区某高考培训机构的一线教师，也加入到这份物理试题的评价：“第24题(物理压卷题)创新地在静电场中放入了一个简谐振动的模型.这个题目给的并不是匀强电场，只是在某方向给了电势的分布，振子在该方向往复运动，已知振子系统机械能的范围是求解振动位移和周期.这个新题型让学生无所适从，除非深刻了解到电势分布与电场(或者力)之间的内在联系和数学关系，否则难以解答.这个题目体现出了整套试题的区分度.”

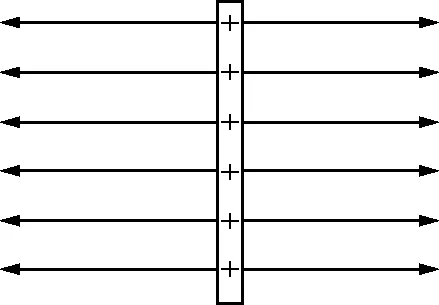
笔者对上述评价提出质疑，认为题目给的就是匀强电场，因为电场线相互平行的电场一定是匀强电场.现用反证法证明，假设“电场线相互平行的电场”不是匀强电场，则电场线疏密分布不均匀，如图1所示.现将一电荷+q从电场中的A点沿A-B-C-D-A路径绕行一周回到A点，对于该过程电场力不做功，即电场力做功为零.但根据图1计算，W总=WAB+WBC+WCD+WDA=WAB+WCD≠0(沿等势面BC和等势面DA移动电荷，电场力不做功，由于电荷在AB处所受电场力大于在CD处所受电场力，故可判断电场力沿AB路径移动电荷所做的正功与沿CD路径移动电荷所做的负功不能完全抵消，即该过程电场力所做的总功不为零.)，推出矛盾，说明假设不成立，即不存在电场线相互平行的非匀强电场.

图1

许多考生对该题之所以感觉到难，除了不能由“已知静电场方向平行于x轴” 判断出电场是匀强电场外，还跟这些考生自认为粒子所做的周期性运动是简谐运动有关(其实高考培训机构的一线教师都以为是简谐运动.笔者认为将“简谐运动”说成“简谐振动”不够恰当).实际上，粒子做的是“匀变速直线运动的往复运动”，回复力由大小恒定的电场力提供.

对命题组提出的第(1)问，由于考生不知道已知电场为匀强电场，故无法根据电势差与场强的关系(U=Ed)列式求解；对第(2)问，需要考生具有较高的数学技巧，将图像中的各物理量整合成相互关联的表达式，同时还需要考生具有较高的数学处理能力；第(3)问是前面两问的综合运用.

笔者根据多年的高中物理教学经验及课题研究，并通过反复斟酌后认为，该题之所以让考生叫难，主要原因是其对该物理过程缺少一个相应的模型映象，当一个错误的映象主导着思维的时候，考生的物理思维必出现卡壳，从而无法对所列问题进行求解.现通过构建物理模型，巧解题.

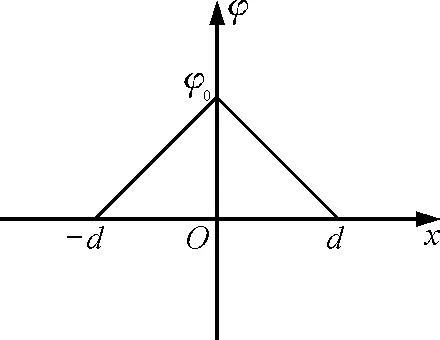
【原题】(2011年高考北京卷)静电场方向平行于x轴，其电势φ随x的分布可简化为如图2所示的折线，图中φ0和d为已知量.一个带负电的粒子在电场中以x=0为中心，沿x轴方向做周期性运动.已知该粒子质量为m，电荷量为-q，其动能与电势能之和为-A(0

(1)粒子所受电场力的大小；

(2)粒子的运动区间；

(3)粒子的运动周期.

图2

解析：(1)因静电场方向平行于x轴，可知电场为匀强电场.根据“逆着电场线电势逐渐升高、顺着电场线电势逐渐降低”，结合图2的信息(从-d到d，电势先由零升高到φ0，接着由φ0降低到零)，可判断y轴左右两侧的电场方向相反.因而想到薄板带电模型，即外表面均匀带正电的薄圆板位于y轴所在平面，其圆心处有一小孔，x轴垂直于薄圆板且穿过该中心小孔.图3为相应的物理模型.

图3

因电场线与等势面垂直，可推知，薄圆板所在平面为同一等势面，其电势等于φ0，故薄板圆心处的O点(即坐标原点)与d点之间的电势差

U=φ0-0=φ0

电场强度的大小

电场力的大小

(2)因粒子的总能量(动能与电势能之和)为负数(即-A)，故粒子的电势能一定为负数，且该负数的绝对值大于动能的绝对值.根据电势能等于电荷量(连同符号)与电势的乘积，又由于该粒子带负电，所以粒子必在电势为正值的电场中做往复运动，由此可推知，粒子只能在x轴上的-d与d两点之间(不含-d与d两点)做往复运动.