巧用图表导向剖析系统误差

郭巍

(韶关市第五中学 广东 韶关 512026)

物理实验的系统误差，涉及实验方案、实验原理、数据处理等理论问题，也涉及器材选择、器材组合、实验操作等技能问题，历来是高考和各类物理考试的高频考点和热门考点.然而，此类考题的得分率却十分低，这一事实说明，分析实验的系统误差，仍是实验教学中的一大难点，有待进一步探究.为此，笔者尝试着用“图表导向法”分析实验的系统误差，即在理论推证的基础上，借助Excel表格及其图表导向功能，赋予推论以具体的数值(理论值或实验值)，将推论进一步数据化、图像化，从而图文并茂、一目了然、动态展现系统误差的成因及其变化规律.现以典型实验的系统误差分析为例，介绍“图表导向法”的具体实施，抛砖引玉以求日趋完善.

1 验证牛顿第二定律实验系统误差的分析

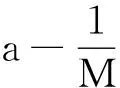
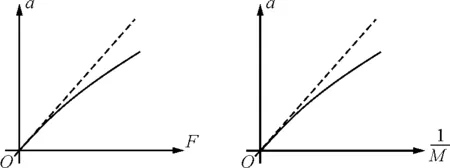
图1 图2

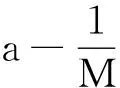
对此，不妨先作简要的理论分析.设图3所示的小车质量为M，砂和砂桶的质量为m，细线的拉力为F.

图3

若以砂和砂桶的重力mg充当小车所受的拉力F，可得小车所受合力的理想值为

F理=mg

小车加速度的理想值则为

然而，实验过程中小车所受的拉力F实和小车的加速度a实，却由动力学方程组

F实=Ma实

mg-F实=ma实

确定，即实验结果应为(不考虑测量误差)

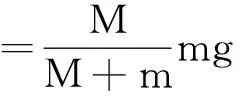
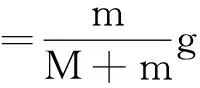
以砂和砂桶的重力mg充当小车所受的拉力F所造成的系统误差为

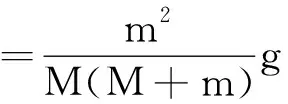
依据上述解析式，虽然可从数学层面上解释系统误差的成因，但这种理性、抽象、甚至枯燥的数学解释，并未有效还原系统误差的物理情境，如果就此打住，学生也未必能真正领悟.为此，笔者进一步借助Excel表格和公式编辑，对上述解析式赋予具体的数值(理论值或实验值)，如表1所示.

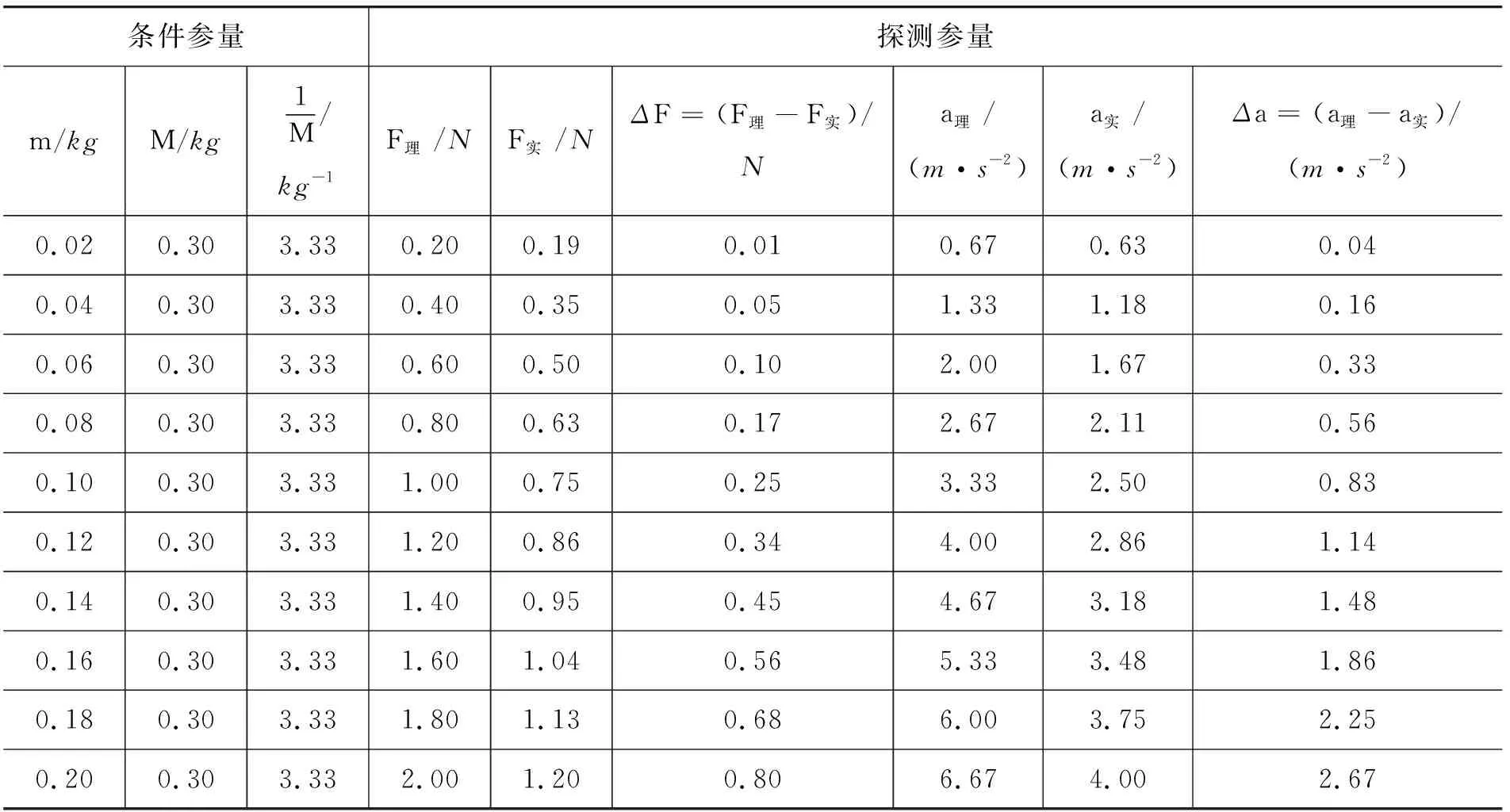
表1 对解析式赋予的数值

表1中，条件参量m和M可贴近实际情况任意设置，其他探测参量则依据上述解析式由公式编辑生成.

再利用图表导向功能，便可将表1中各参量的关系图像化.任意改变条件m或M，其他探测参量都随之变化，所对应的图像也随之动态变化，图4至图7便是在不同条件下由表1派生的部分变量关系图像.

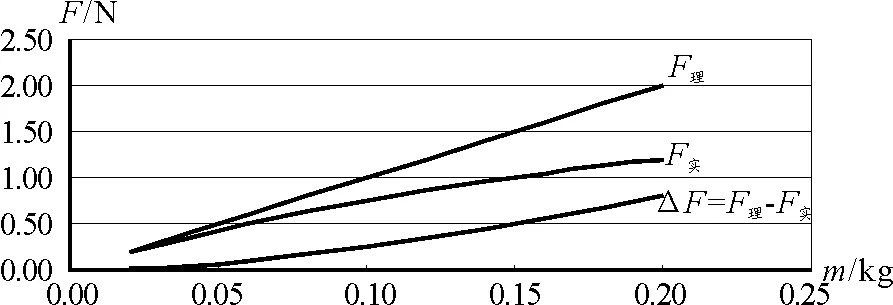
图4 M一定时 F-m图像

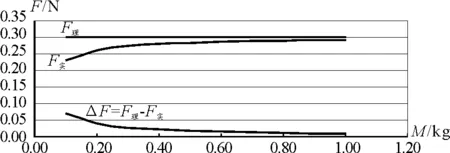
图5 m一定时 F-M图像

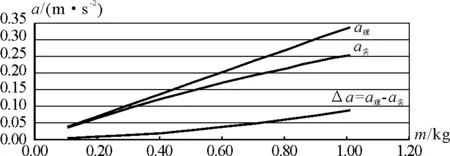
图6 M一定时 a-m图像

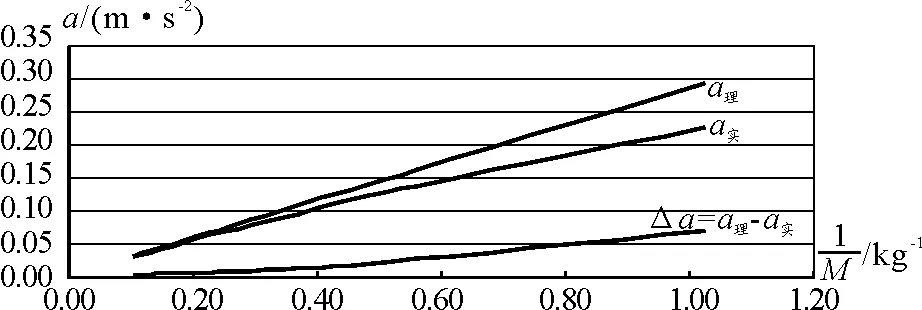
图7 m一定时图像

相对解析式而言，图4至图7更能一目了然地看出,小车所受的拉力F小于砂和砂桶的重力mg，用砂和砂桶的重力mg代替小车的合力F，所造成的系统误差随m和M的变化而变化，m偏大而M偏小，系统误差ΔF和Δa越大；只有当m较小而M较大，即只有当m≪M时，砂和砂桶的重力mg才近似等于小车所受合力F，a实才趋近于a理.因此，利用图3所示的实验装置验证牛顿第二定律，必须尽量使m≪M才能有效地减小系统误差.

2 伏安法测电阻系统误差分析

用“图表导向法”剖析伏安法测电阻的系统误差，所生成U-I图像如图8至图10所示(方法与上类同，不赘述).

图8 Rx=10 Ω时 U-I图像

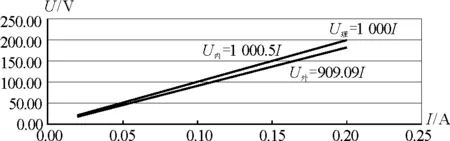
图9 Rx=1 000Ω时 U-I图像

图时 U-I图像

观察U-I图像明显看出当被测电阻较小时，电流表外接法所测得的U-I图像与理想电表所得的U-I图像几乎重合，所测的电阻值稍小于实际的电阻值，电表造成的系统误差很小；而电流表内接法所测得的U-I图像与理想电表所得的U-I图像却有明显偏差，所测的电阻值明显大于实际的电阻值，电表造成的系统误差偏大.

当被测电阻较大时，电流表内接法所测得的U-I图像与理想电表所得的U-I图像几乎重合，所测的电阻值稍大于实际的电阻值，电表造成的系统误差很小；而电流表外接法所测得的U-I图像与理想电表所得的U-I图像却有明显的偏差，所测的电阻值明显小于实际的电阻值，电表造成的系统误差偏大.

3 伏安法测电动势和内电阻的系统误差分析

用“图表导向法”分析伏安法测电动势和内电阻的系统误差，可生成图11,图12所示的U-I图像(方法与上类同，不再赘述).

图11 电流表内接法 U-I图像

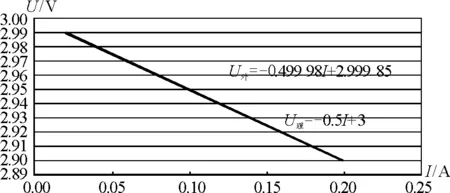
图12 电流表外接法 U-I图像

从图11和图12可明显看出,电流表内接电路所测得的电动势等于实际的电动势，但由于电流表内阻和电源内阻较为接近，实验测得的内电阻与其实际内电阻相差较大；电流表外接电路所测得的电动势和内电阻虽然都偏小，但都十分接近实际值，即电流表外接电路更有利于减小系统误差.因此，中学物理实验必须选用电流表外接电路测量电源的电动势和内电阻.

综上所述可知，“图表导向法”集信息技术、误差理论、变量调控、图表演示为一体，不仅方法科学、数据准确，而且可任意调控系统误差要素，图文并茂、一目了然、动态展现系统误差的成因及其变化规律，因而十分便于学生理解，取得令人满意的教学效果.