太阳与行星间的引力教学案例

陆小华

(苍南县矾山高级中学 浙江 温州 325807)

1 案例背景

2011年3月14日，笔者有幸参加了浙江省苍南县灵溪第二高级中学举行的“特级教师伴我行”物理教学活动，聆听了一位特级教师的精彩示范课——太阳与行星间的引力.课上虽然没有采用媒体教学，但是凭借教师深厚的物理教学功底，幽默风趣的语言，特别注重培养学生的逻辑推理能力，强调大胆质疑与猜测，小心求证，使一节本来很枯燥与艰深的物理理论课变得生动活泼，深深吸引和感染了学生，赢得了同行与学生的阵阵掌声.由于课时进度的关系，一个星期后，笔者按照该教学理念与教学思路做了稍稍改动，在施教的班级模拟，但课上不但没有掌声，反而实效性比平时都差，学生一点兴趣都提不起来.面对这种尴尬的局面，笔者重整思路，第二天，在大胆的改动与尝试下，效果非凡.

2 教学描述

2.1 凸显模型构建

师：前面我们研究了行星运动的三定律，请同学们用自己的语言来描述一下.

生：椭圆轨道定律、等面积定律、半长轴立方比周期平方定律.(开普勒三定律)

点评：化教师主导为学生主体，让学生有话说，在理解学科知识的基础上养成知识内化的习惯，同时为这一节的引入打下伏笔.

师：既然行星运动的轨道是椭圆，那么要做怎样的处理才能求出椭圆运动加速度公式呢？

生：把它看成圆周运动或匀速圆周运动，把轨道微分为无数个圆弧……

师：微分为无数个圆弧的方法很好，但是我们只能找到该圆弧上的向心加速度规律，没有普遍性，而看成圆周运动则要“大胆”，你敢吗 ？看成匀速圆周运动则要“胆大包天”！

学生陷入了沉思.

点评：对每一个学生做到合理点评，以激励为主.激发学生大胆猜测.

师：其实，看成圆周运动是很科学的.我们一起来看看八大行星运动的轨道数据，找找有什么规律.

媒体出示表1.

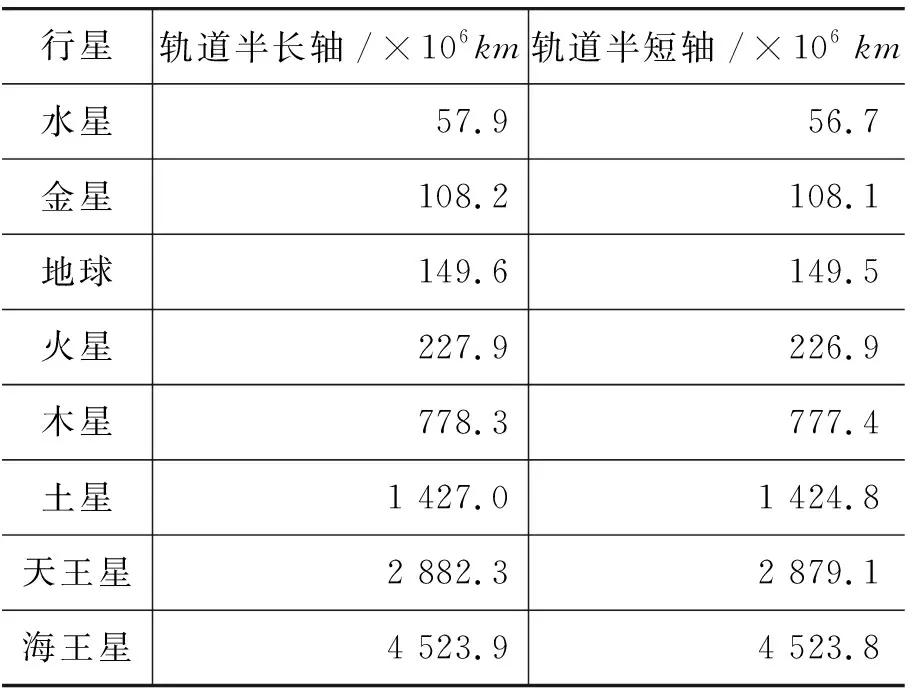
表1 八大行星轨道数据

生：半长轴与半短轴几乎相等.

师：你这“几乎”二字，我倒觉得差蛮远的！为什么呀？

生：单位是106km .

师：那对嘛？为什么？

生：对吧！相对于半长轴、半短轴的长度来讲，是一个很小的量.

师：对，我也是这么想的，真是“英雄所见略同”.

生：哈哈……

点评：忽略次要，突出主要，小心求证，让学生在大胆猜测的过程中形成缜密的逻辑思维.

师：那凭什么可以看成是“匀速”圆周运动呢？大家找找自己的理论依据.

学生相互讨论，说不出什么道理.

师：看作圆周运动，请问你把太阳的位置搁哪？

生：圆心啊！

师：那这时候开普勒的三定律我们怎样简化？

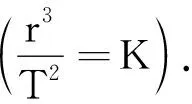
师：要我说就两个:匀速圆周运动定律，半径立方比周期平方定律.

学生用兴奋的眼光看了看……

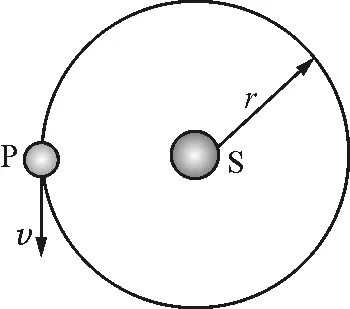
图1

师：我们一起来构建这个运动模型好不好？

媒体出示匀速圆周运动动态模型,如图1所示.

点评：层层递进，凸显模型构建过程，教给学生处理问题的方法.

2.2 将“大胆”进行到底

师：行星做匀速圆周运动需要几个条件？

生：两个，线速度与向心力.

师：向心力由谁来提供呢？

生：太阳对行星的引力.

师：大家的胆子挺大的！可物理学史上不是那么一帆风顺.首先我们来了解几代人的观点.

教师边讲边媒体展示:

(1)伽利略：一切物体都有合并的趋势，这种趋势导致物体做圆周运动;

(2)开普勒：受到了来自太阳的类似于磁力的作用;

(3)笛卡儿关于行星的周围有旋转的物质(以太)作用在行星上，使得行星绕太阳运动；

(4)胡克、哈雷等关于受到了太阳对它的引力，证明了如果行星的轨道是圆形的，其所受的引力大小跟行星到太阳的距离的二次方成反比，但没法证明在椭圆轨道规律也成立；

(5)牛顿关于如果太阳和行星间的引力与距离的二次方成反比，则行星的轨迹是椭圆,并且阐述了普遍意义下的万有引力定律.

生：对“以太”物质存在的想法，觉得很荒谬.

点评：对学生进行物理学史教育，培养科学探究不畏艰辛的品质，形成科学的世界观.

师：今天我们就追寻牛顿的足迹，探讨太阳对行星的引力与哪些因素有关.

2.2.1 太阳对行星的引力FSP

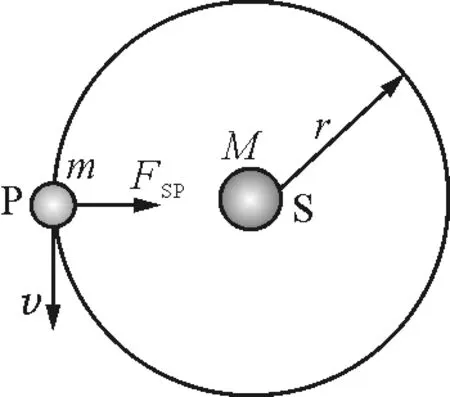
图2

媒体展示静态模型情境(图2).设某颗行星的质量为m，速度为v，行星到太阳的距离为r，则行星绕太阳做匀速圆周运动的向心力由谁来提供,需要多大？

师：我们一起来推导，老师可能会犯错误，你们一定要帮帮我哟！

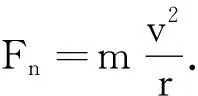
师：在当时，线速度v是无法测量的，那么在天文观测中应该怎样表示向心力呢？

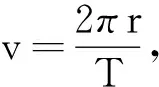
师：现有个疑惑，从表达式看，太阳对行星的引力应该与半径r成正比，而胡克说“引力大小跟行星到太阳的距离的二次方成反比”，问题出在哪儿呢？

生：这里周期T不是定值，所以不能这么说.

师:谢谢你们帮了个大忙，解决了我这个困惑.那什么情况下与距离的二次方成反比？接下来该如何解决这个问题？

点评：充分肯定与相信学生，用诙谐的语言把问题在和谐的气氛中抛给学生，化学生被动为主动，拉近师生之间的距离.

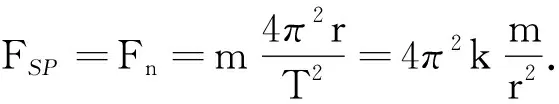
生：可以，因为m是行星的质量，k是个常数.

师：很好，但是要知道这个常数k与什么有关啊.

生：中心天体，太阳啊！

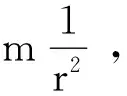
点评：小心求证，大胆拓步.k的相关要素的涉及为接下来讨论行星对太阳的引力打下伏笔.

2.2.2 行星对太阳的引力FPS

师:太阳对行星有引力作用，那么行星对太阳是否也有引力呢？你的理论依据是什么？

生：当然有，作用力与反作用力的关系 (牛顿第三定律).

点评：问题转化，引出行星对太阳的引力FPS探讨，让学生应用物理规律，活学活用.

师：行星对太阳的引力与哪些因素有关呢？我们应该以谁为研究对象？

生：太阳的质量M, 太阳到行星的距离r, 以太阳为研究对象.

点评：让学生学会类推的研究方法，大胆尝试.

师：行星对太阳的引力FPS怎么表示？

图3

媒体出示静态模型(图3).

师：表达式里k与前面一样吗？若不一样怎样修改？

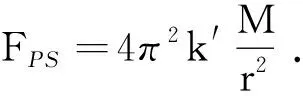
2.2.3 太阳与行星间的引力F

师：现在，我们来归纳一下太阳与行星间的引力有关的几个因素.

生：行星的质量m，太阳的质量M,它们之间的距离r.

点评：培养学生概括，以及综合处理问题的能力，拓展到本节要解决的本质问题,太阳与行星间的引力F.

师：如何定性地写出太阳与行星间的引力F的表达式？

师：凭什么说是Mm呢？(M+m)难道不行吗？

学生兴奋地看着教师，微笑着，表情很“无奈”，又一次陷入了沉思.

师：我们不妨从前面两个力之间的关系找找理由.

点评：关键时刻，合理引导，又一次拉近师生之间的距离.

生：FSP=FPS.

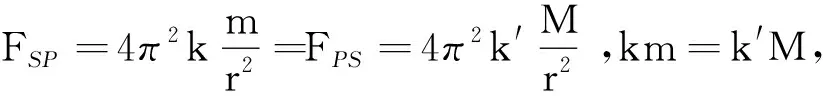
师：这里边k,M与谁有关？k′,m又与谁有关?

生：k,M仅仅与太阳有关，k′,m仅仅与行星有关.

师：太阳系有八大行星，如果是另外的一颗行星,关系式会如何？大家猜想一下有怎样的规律.

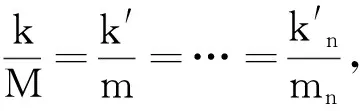
点评：降低台阶，合理引导，激发学生的大胆猜测.

点评：合理质疑，培养学生缜密的逻辑思维能力.

师：那么把k或k′带入又会有怎样的发现？

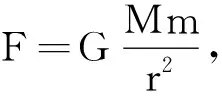
点评：激励学生，用欣赏与发展的眼光来看待学生.

师：我们一起来总结一下太阳与行星间的引力.

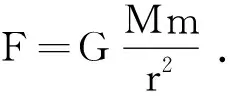
师：这里边各个符号的物理含义是什么？

媒体出示静态模型图4.

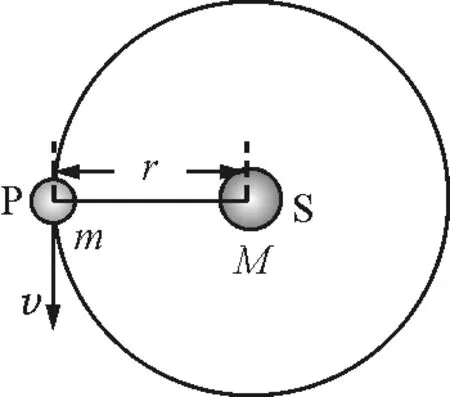
图4

师生：M为太阳的质量，m为行星的质量，r为行星到太阳的距离或者是轨道半径(强调不是天体半径R)，G为引力常量，与行星、太阳均无关.

太阳与行星间的引力是一对作用力与反作用力，大小相等方向相反,在二者的连线上；使用范围为太阳与行星间的引力.

点评：充分理解牛顿的引力定律，突出重点.

2.3 走出课堂遐想无限

师：除了太阳对行星有引力外.其他行星之间是否也存在引力呢？

生：有吧!应该也满足牛顿引力定律.

师：很好！其实这也是导致行星运动轨道是椭圆的直接原因.大家已经有了大胆猜测的习惯，下一节中我们将会用实验加以检验.

师：除了天上的物体(天体)之间存在引力，那么人间(地上)的万物呢？比方你与同桌之间？

生(微笑着)：有啊！

师(指着一个男生一个女生)：那你们俩怎么没有吸在一起？

生(赶紧给自己找理由)：因为我们的质量很小啊！呵呵呵！

师：看来，同学们已经完全理解了牛顿引力定律，无形中把它推广到了宇宙的万物，非常了不起！确实，牛顿的引力定律统一了天上与人间，具有普适性与统一性.

师：其实，今天我们就解决了一个问题，向心力的问题.那速度呢？天体的初速度由谁提供呢？

生(非常好奇)：天生的吧！上帝给的！宇宙大爆炸？不知道！

师：大家非常了不起.当时很多科学家就是这么想的，包括牛顿.晚年的他在研究行星为什么会围绕太阳运转时，由于信奉上帝，认为除万有引力的作用外，还有一个“切线力”，这个“切线力”只能是来自上帝的“第一推动力” ，从而研究神学，走入歧途！那是多么的遗憾啊.直到今天，仍然是仁者见仁，智者见智.课后同学们可以结合网络或科普作品，互相探讨.

点评：让学生从教材中走出来，依托科学的魅力产生无限的想象，体现物理思想的美丽.

4 总结

这是一节能充分体现教师新课程理念的理论探究课.教师深入地解读了教材与教学指导意见，课上对教材做了大胆的尝试，采取了知识点细化和分层，很好地落实了三维目标.课堂上，师生融为一体，学生思维紧张而又活跃,行动上忙碌而又充实,心情上放松而又愉快，最大限度地参与了学习过程，充分体现了“教师主导，学生主体”的新课程理念.教师通过设计一系列问题情境引导学生讨论、分析、大胆猜想和逻辑推理，让学生通过解决问题参与学习过程.本案例中教师用的最多方法是巧设问题情境，让学生大胆地质疑与猜测，培养了学生“小心求证”和缜密的逻辑推理能力，激发了学生学习物理的兴趣，充分调动了学生学习的积极性.