张宗燧对约束系统量子化的贡献
2011-01-25尹晓冬
尹晓冬
(首都师范大学 物理系,北京 100048)
朱重远
(中国科学院 理论物理研究所,北京 100190)
在将经典动力学体系从拉格朗日形式导出哈密顿形式以进行正则量子化时,常常由于开始的拉格朗日形式中的动力学变量不都是独立的(即存在着约束),从而不能直接用通常的方法去实现自洽的量子化,这就是需要研究约束系统量子化方案的原因。实际上,约束系统的量子化是当代理论物理在建立基本的动力学时用到的最重要的关键工具之一。我们知道,从现象学角度,自然界存在着四种基本相互作用:强相互作用、电磁相互作用、弱相互作用和引力相互作用。在现在已经建立的正确地描写了强作用、电磁作用和弱作用的标准模型中,描述强作用的量子色动力学,描述电磁作用及弱作用的电弱统一理论(包括描述电磁作用的量子电动力学),都涉及到约束系统的量子化。甚至于在至今尚未建立满意的量子理论的引力相互作用的研究中,其主要的尝试方案,如弦理论、阿什特卡(Abhay V.Ashtekar,1949—)的非微扰量子引力等也都使用了约束系统的量子化方法。所以建立约束系统的量子化方法,在物理学理论研究中,占据十分重要的地位。
目前理论物理界广泛使用的约束系统的量子化方法,主要可以分为二类。一类是由狄拉克(Paul Adrie Maurice Dirac,1902—1984)于1950年开始的工作基础上发展起来的正则量子化方案[1—3],另一类是在由1967 年法捷耶夫(Ludwig.D.Faddeev,1934—)和波波夫(Victor.Nikolaevich.Popov)的工作开始的用路径积分量子化方法发展起来的方案,后者对解决非阿贝尔规范场论的量子化作出了重大贡献[4]。本文打算探讨的是,在这些方案建立之前,中国理论物理学家张宗燧①张宗燧(1915—1969),中国理论物理学家。1934年毕业于清华大学物理系并留校攻读研究生一年。1936—1938年在英国剑桥大学数学系跟随著名理论物理学家福勒教授攻读博士学位,1938年获得哲学博士学位,其后去丹麦、瑞士、法国等地进行科学研究。1940年回国任重庆中央大学物理系教授。1946年以英国文化协会高级研究员身份赴英国剑桥大学进行科学研究。1947年赴美国普林斯顿高等研究院(Institute for Advanced Study in Princeton)、费城卡内基理工学院(Carnegie Institute of Technology)访问。1948年回国,历任中央大学、北京大学、北京师范大学教授及理论物理教研室主任,中国科学院数学研究所研究员及理论物理研究室主任,兼中国科技大学教授等职。1957年受聘为中国科学院数理化部学部委员(今中国科学院院士)。文革期间受迫害自杀。在1944—1946年期间完成的工作[5—7],尽管所提的方案与上述二类不同,但已是一种自洽的行得通的方案。所以,张宗燧对约束系统的正则量子化方法做出了重要的贡献。
1 张宗燧工作之前的约束系统量子化研究
1.1 问题的提出
实际上,在量子场论刚建立时,就遇到了约束系统的量子化方法问题。大家知道,人们首先认识到的经典场是麦克斯韦电磁场。要建立电磁场及电磁相互作用的微观理论,就需要将其量子化。历史上,最早成功地建立的量子场论就是1927年狄拉克给出的[8]量子电磁场场论。狄拉克的基本做法是将辐射场分解成简谐振动,并将电磁场的量子化归结为这些基本振动的量子化。由于这一方案中,电磁势的横场与纵场及标量场的量子化处理处于不同的位置,所以理论并不明显地协变。随后,1929年海森堡(Werner Karl Heisenberg,1907—1976)和泡利(Wolfgang Pauli,1900—1958)建立了一般场论的正则量子化方式[9—10]。但是,当用他们的方法去处理电磁场时,会立刻发现与电磁标量势共轭的正则动量为零,也就是说,正则自由度不都是独立的,它们存在着约束。如果直接使用普通的正则量子化方法,将立刻出现零算子的对易关系不为零的矛盾。显然,在这种情况下,哈密顿函数及正则对易关系等都不可能按普通的方法直接使用,必须进行处理。
1.2 罗森菲尔德和狄拉克的早期方案
最早提出的一些对电磁场进行量子化的修正方案存在着明显的令人不满意之处。正如罗森菲尔德(Leon Rosenfeld,1904—1974)在泡利的指导下于1929年完成并于1930年发表的文章[11]中提到的:海森堡和泡利提出的第一种方法,是在拉格朗日函数中加入带小参量ε相关的项,从而使得正则共轭动量都不为零,最后再令ε趋于零,这一方案破坏了明显的规范不变性;海森堡和泡利提出的另一种方案,是取标量势为某限定值去减少方程,此做法对四度矢量的不同分量没有作同样的处理,从而使量子理论的相对论不变性的证明变得很困难;费米(Enrico Fermi,1901—1954)提出的方案,是在拉格朗日函数中附加新项,使得共轭动量不为零,但为了使最终的运动方程与原来的系统的方程一致,又必须加上约束([10],175页)其结果的形式也没有明显的规范不变性。
罗森菲尔德在文[11]中为解决此问题提出了的方案如下:
对于像电磁场这样的有规范群对称性的体系,用不定乘子λr与约束

去构造哈密顿函数

于是,基本方程由用此哈密顿函数构造的正则场方程及对易关系,加上约束方程组成。但是,由于这组方程中明显包含着拉格朗日未定乘子λr,它们是未知的,完全可能是动力学的。因此,对它不加处理,是无法实现量子化的。
狄拉克于1933年发表了《经典力学中的齐次变量》一文[12]。在这篇文章中狄拉克从比电磁场更一般的角度提出了约束系统问题。他举出了静止质量为零的自由粒子的相对论性运动作为另一个例子。此文中他建议的用齐次坐标写出的正则形式的运动方程是

其中ρa,ρb等是拉格朗日不定乘子。实际上,由于这些不定乘子是未知的,所以此形式也不能直接用于量子化。
关于拉格朗日不定乘子需要进行处理才能进行量子化的问题,是张宗燧首先指出的,具体论述详见下文。
2 张宗燧的贡献
2.1 三篇关于约束系统量子化论文的发表情况
根据张宗燧发表的论文统计[13]可知,张在1945年到1947年期间发表的7篇文章中除1篇是关于合作现象外其余6篇是与粒子物理及量子场论相关的,其中有三篇[5—7]是关于约束系统量子化方面的,这三篇分别是:
(1)A note on the Hamiltonian theory of quantization(《哈密尔顿量子化理论的一个注记》),Proc.Roy.Soc.of London,1945;
(2)A note on the Hamiltonian equations of motion(《哈密尔顿运动方程式的理论的一个注记》),Proc.Camb.Phil.Soc,1946;
(3)A note on the Hamiltonian theory of quantization(II)(《哈密尔顿量子化理论的一个注记(II)》),Proc.Camb.Phil.Soc,1947。
下文依次简称为第一、第二、第三篇论文。这些论文发表时直接注明了,第一篇收录于1944年7月11日,第二篇收录于1945年9月24日,第三篇收录于1946年6月7日。第一及第二篇论文所署地址均为“Central University,Chungking”(重庆中央大学),第三篇所署地址为剑桥。由于张宗燧是1946年再次前往剑桥进行学术访问的,所以可以断定张宗燧是在中央大学期间开始从事约束系统量子化方面研究的。1937年10月,由于日本侵华中央大学不得不从南京迁到重庆,张宗燧的这些研究,正是在抗日战争期间的重庆那十分艰苦的条件下开展的。这一点可以从冯端①冯端(1923—),浙江绍兴人,生于江苏苏州。固体物理学家。1946年7月毕业于中央大学理学院物理系并留校。1949年该校更名为南京大学后,历任物理系副教授、教授及固体物理研究所所长,研究生院院长,1985年起任固体微结构物理国家重点实验室主任兼学术委员会主任。1980年当选为中国科学院院士。的回忆中得到佐证。冯端是张宗燧在重庆中央大学的学生,1943年冯上大学二年级时所选的热力学和理论物理课程就是由张宗燧讲授的②据冯端回忆,当时讲授的理论物理内容是经典电动力学加相对论,参考Abraham&Becker的电动力学。1957年张宗燧出版的《电动力学与狭义相对论》可能就是由当年讲课笔记扩展而来的。。在《松林坡往事》一文中,冯提到了当时上课的情景:
中大(中央大学)校舍极差,教室、宿舍都是草顶平房,比同在沙坪坝的重庆大学和中央工业学校都差,更比不上抗战前的南开中学。但是简陋校舍中的学术空气却是浓郁的。
……
值得注意的是即使在抗战的万分艰苦阶段,中央大学物理系的一些教授们还埋头进行科学研究,而且取得了一些难能可贵的成绩。……在重庆时代,埋头研究工作的还有张宗燧教授,他在剑桥大学师从R.H.Fowler教授,进行统计物理合作现象理论的工作,取得了不少成就。1940—1945年在中央大学执教期间还在国际刊物上发表了三篇这方面研究工作的论文。但是值得注意的是,在这段时期他已将研究重心转移到量子场论这一领域,也发表了由P.A.M.Dirac推荐的三篇文章。这成他后期工作的主要领域。连同前面的一些工作,表明他在重庆中央大学时期的研究硕果累累。[14]
值得提到的是,这三篇文章中,第一篇和第二篇发表时编辑部都注明了是由狄拉克推荐的(Communicated by P.A.M.Dirac)。张宗燧在第二篇和第三篇文章末尾都写到:“最后,笔者要感谢狄拉克教授对本项工作的兴趣。”“感谢他对此极大的兴趣并与我的讨论,这让我受益匪浅。”③英文原文分别是:“In conclusion,the writer wishes to thank Prof.P.A.M.Dirac for his interest in the work.”及“In conclusion,the writer wishes to thank Prof.P.A.M.Dirac for his kind interest and discussion,for which the writer is greatly indebted.”表明张宗燧的工作与狄拉克有密切关系。
在这里顺便指出,在学术上张宗燧与狄拉克一直到1950年都保持着比较紧密的联系。抗战胜利后,张宗燧由中英文化协会李约瑟(Joseph Needham,1900—1995)安排,以高级研究员的身份于1946年1月去剑桥大学,也是由狄拉克安排在剑桥大学讲授量子场论④“剑桥大学报告”(Cambridge University Reporter)中的学术管理委员会1947—1948年度报告(Annual Report of the Board of Research Studies)上面记录:Mr Chang开设Quantum Mechanics of Fields(量子力学场论),P470,英国剑桥大学图书馆。。1946年底狄拉克计划去美国讲学,张宗燧随狄拉克一块去了普林斯顿高等研究院,并在费城卡内基理工学院做访问学者。即使张宗燧回国后,50年代张宗燧与狄拉克依旧保持学术上通讯联系①1949年9月、1950年1月、1950年9月张宗燧与狄拉克的通信,英国剑桥大学丘吉尔档案馆。。
2.2 三篇论文的内容分析
下面来分析研究张宗燧的三篇有关约束系统量子化的论文。从内容上看,第三篇总结了前二篇的主要内容,所以在这里主要对第三篇论文展开分析。
首先,在此文中,张宗燧直接指出:狄拉克1933年的文章虽然“证明了运动方程总可以纳入正则形式,但是,最终的方程仍包含着未知拉格朗日乘子,因此不能用于过渡到量子理论”②英文原文是:“It was shown that the equations of motion can always be put in canonical forms.However,the final equations still contain quantities of the nature of unknown Lagrange multipliers,and are thus not suitable for passing to a quantum theory.”。这是有关拉格朗日乘子的十分明确的论断,也是目前所看到的第一次提出这个问题的文献。问题直接所指的虽是狄拉克的文章,但显然,此前的用拉格朗日乘子的工作,也有同样的问题。
其次,张的这篇文章讨论了更一般的约束系统。事实上,他首先讨论的是对外加约束条件(即不是由拉格朗日的正则共轭动量为零所产生)的系统的处理。他指出,对于

如有f个外加附加条件

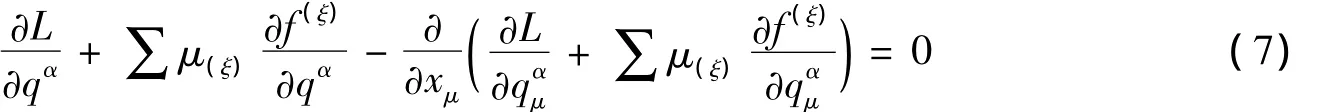
则有方程其中μξ是拉格朗日乘子,(6)式和(7)式是场方程。这里的记号中,xμ=(x,y,z,ict),x=(x,y,z),μ,υ,… 取值为(1,2,3,4),r,s,… 取值为(1,2,3),qα是独立变量,qαμυ=(∂/∂xμ)(∂/∂xυ)…qα。为了导出正则形式,他的做法不是通过拉格朗日去定义动量,而是设

其中 bα是 pα,qα,,x 的函数,它与一起由下列二式确定:

用此哈密顿函数写下的正则方程为

此式展开是

容易证明(9)、(10)、(12)、(13)与(6)、(7)完全等价。这里,需再强调一下,原来的拉格朗日乘子已经变为 ηξ,它与 bα都是由(9)、(10)式确定的 (pα,qα,qαr,x)的函数,不是未知量。所以,这里的方程中不再有未知量,用这些形式可以实现量子化。
在这里笔者还愿意顺便指出,这篇论文还提出,对于(5)—(7)式的系统,可以考虑定义新的拉格朗日为

然后,将拉格朗日乘子μξ也看成是与其他坐标一样的动力学变量,于是,μξ的共轭动量为零,系统成为共轭动量为零的约束类型。这一提议在当时也是很有创意的。
对于只有正则动量为零的约束的系统,这篇文章的处理方法如下:
动量的定义如通常一样,
设为零的动量是Pl,相应的坐标为Ql。其他的无约束的动量和坐标记作 (p,q)。
于是,



确定。可以证明,由此导出的正则方程与(16)、(17)、(18)等价。对于(19)式完全独立,从而可以用p,q,x定出Bl及bα的情形,只需令p,q取正则对易关系即可,Ql则可以根据运动方程看作Bl。于是,可以用Bl与p,q的函数关系给出Ql与p,q的泊松括号,进而完成量子化。
对于(19)式不完全独立从而不能用p,q,x定出Bl及bα的情形,情况比较复杂。此文讨论了其中一类情形,即其拉格朗日量在部分坐标作如下变换时不变①注意张宗燧的这篇文章中将此变换称为“规范变换”,但实际上并不是大家所称的规范变换。它只是与规范变换有相似处的一类变换。的体系:

经过分析,可以证明此时必有若干相应的动量为零。对于这些动量和坐标,在用了一些技巧后,又可证明其(18)式可以用某些动量的函数为零的条件所代替:

然后,此文研究了(∂gu(p)/∂x4),说明它可以用(16)、(17)式表示为 Ql,qα,pα的函数,并进一步证明了,如果(∂gu(p)/∂x4)不恒为零,运动方程将不自洽,相应的体系是非物理的,不必考虑。对于∂gu(p)/∂x4=0的情形,(18)或(21)式完全可以作为初始条件。于是,这类体系的哈密顿形式可以这样来建立:
以上论述比较仔细地论述了张宗燧对约束系统量子化的处理方案。下面再进一步做几点评论:
(1)张宗燧明确指出:如果使用了未知拉格朗日乘子,就不能直接进行量子化,因此,必须正确处理拉格朗日乘子,这是十分重要的。既然张的这些文章与狄拉克讨论过,甚至由狄拉克推荐发表,由此可以推断,他的这一意见是狄拉克认可的。事实上,在后来的工作中[1—3],狄拉克对拉格朗日乘子进行了认真的分析和处理。
(2)张宗燧的研究不仅限于电磁场。他既考虑了由拉格朗日量的具体形式决定的没有共轭动量产生的约束,也考虑了不是由拉格朗日导出的外加约束条件。原则上外加条件可以有多种类型,因此,他所考虑的系统是相当广泛的。
(3)形式上看,张宗燧的方案与后来的狄拉克的方案不相同。但是,分析和检查张的方案,可以发现,张的方案的确解决了直接使用普通方法所存在的矛盾,是可行的。张的方案中用新的变量作为正则变量,满足正则泊松括号,因此,老变量的泊松括号不再是正则关系从而不与约束条件矛盾。狄拉克的方案则是定义新的括号①现在称为‘狄拉克括号’。使之不与约束条件矛盾。
(4)张的文章中,在将经典的初始条件(18)式量子化时不作为算子方程,而是作为对于物理状态的条件(22)式。但现在知道,(18)式量子化时对应的条件可以比(22)式更弱,只要它在物理态间的矩阵元满足条件即可。
在这一节结束的时候,需要再次强调,以上对张的方案做如此详细的讨论,是为了这节也是这篇文章的主旨,即说明张的方案确实对一大类约束系统是自洽可行的。
3结语
张宗燧是中国最早开展量子场论研究的理论物理学家之一[15]。本文论证了张宗燧于1944—1946年期间对约束系统量子化做出的重要贡献:首先指出了必须正确处理拉格朗日乘子,并提出了可行的量子化方案。
我们对在张宗燧的这些工作之前的对于约束系统量子化开展的研究进行了文献搜索,未发现比之更早的有关约束系统量子化研究中提出需要对拉格朗日乘子进行处理的论述。同时,积极与国外学者交流,并向国内外专家广泛地征求信息,迄今为止,还未发现有比张宗燧的文章更早的自洽的约束系统量子化方案。基于以上情况,张宗燧极为可能是国际上第一个提出可行的解决了拉格朗日乘子问题的量子化方案的物理学家。
致 谢本文部分内容在2009年12月于北京工业大学举行的“理论物理前沿研讨会”以及2010年6月于德国柏林举行的“第三届国际量子力学史会议”上报告过,作者对于这两个会的参加者的兴趣和热烈讨论及建议表示感谢。
作者感谢中国科学院理论物理所戴元本院士的多次仔细的讨论,感谢美国衣阿华州大学杨炳麟教授,北京大学宋行长、马伯强教授,中国科学院理论物理所李淼、刘寄星教授,北京工业大学黄永畅教授,南京大学王凡教授等的兴趣和讨论,感谢德国马克斯·普朗克科学史研究所Donald Salisbury教授提供罗森菲尔德论文的原文复印本及英译本。作者之一尹晓冬对在访问马克斯·普朗克研究所、英国剑桥大学、丹麦玻尔档案馆、英国李约瑟研究所期间得到的帮助与支持表示诚挚感谢。
1 Dirac P A M.Generalized Hamiltonian dynamics[J].Canad.J.Math,1950,2:129—148.
2 Dirac P A M.The Hamiltonian Form of Field Dynamics[J].Canad.J.Math,1951,3∶1—23.
3 Dirac P A M.Lectures on Quantum Mechanics[M].New York:Yeshiva University,1964.
4 Fadeev L D,Popov V N.Feynman diagrams for the Yang-Mills field[J].Phys.Lett,1967,25B∶29—30.
5 Chang T S.A note on the Hamiltonian theory of quantization[J].Proc.Roy.Soc.of London,1945,A183∶316—328.6 Chang T S.A note on the Hamiltonian equations of motion[J].Proc.Camb.Phil.Soc,1946,42∶132—138.
7 T.S.Chang.A note on the Hamiltonian theory of quantization(II)[J].Proc.Camb.Phil.Soc,1947,43∶196—204.8 Dirac P A M.The Quantum Theory of the Emission and Absorption of Radiation [J].Proc.Roy.Soc,1927,A114∶243—265.
9 Heisenberg W,Pauli W.Zur Quantendynamik der Wellenfelder[J].Zeits.Physik,1929,56∶1—61.
10 Heisenberg W,Pauli W.Zur Quantendynamik der Wellenfelder[J].Zeits.Physik,1930,59∶168—190.
11 Rosenfeld L.Zur Quantelung der Wellenfelder[J].Annalen der Physik,1930,5∶113—152.
12 Dirac P A M.Homogenous variables in classical dynamics[J].Proc.Camb.Phil.Soc,1933,29∶389—400.
13 张宗燧论文选集·附录:张宗燧论著目录[C].张宗燧先生诞生九十周年纪念会,2005.
14 冯端.松坡林往事[A].施士元.施士元回忆录及其他[M].南京:南京大学出版社2007.179—182.
15 戴元本.中国量子场论研究的初期[J].现代物理知识,2009,21∶64—65.
