基于非采样Contourlet变换和SVD的数字水印算法研究

马 婷，黄剑华，赵 勇，周卫红

(1.云南民族大学数学与计算机科学学院，云南昆明650031;2.广西工学院信息与计算科学系，广西柳州545006)

数字水印技术是将版权信息嵌入到原始数字媒体产品中，起到版权保护的作用．数字水印算法主要分为空间域算法和变换域算法两大类，其中变换域算法比空间域算法具有更好的鲁棒性，常见的变换域算法有DFT、DCT和DWT，DCT是JPEG压缩标准的核心算法，DWT为JPEG2000压缩标准的核心算法，然而这些算法都难以抵抗几何攻击．2002年，Do和Vetterli［1－2］提出的Contourlet变换不仅具有小波变换的多分辨率和时频局部性还具有多方向性和各向异性，能很好地捕捉图像的几何特征，而小波变换只能捕捉水平、垂直和对角线方向的信息，但由于Contourlet变换的拉普拉斯塔式分解和方向滤波器组存在下采样过程，使得Contourlet变换不具有平移不变性，而且采样可引起低频频谱泄露，变换后使得低频部分与高频部分存在频谱混淆的现象，也易丢失子带的方向信息．2005年，Do和Cunha［3－4］提出的非采样Contourlet变换不但具有Cont-ourlet变换的特性，弥补了Contourlet变换的不足，而且更能准确地提取和表示图像的几何特性，计算也更加准确，同时非采样Contourlet变换又是高冗余度的Contourlet变换，所以基于非采样Contourlet变换的水印算法嵌入的信息量更大．

文献［5］对图像进行了Contourlet变换后，对低频子带进行分块奇异值分解，通过图像的重要特征构造水印信息，该算法选择在变换后的低频嵌入水印，低频子带能够满足人们视觉质量的要求，所以在低频子带上嵌入水印本身可满足水印的不可见性，若对图像进行信号处理后对低频子带的影响也较小，但该算法采用零水印算法，算法计算量较大，且对大的图像可行性不大．文献［6］同样首先对图像进行Contourlet变换，选择在中频嵌入水印，该算法选择中频系数嵌入水印，虽然中频部分含图像的纹理等细节信息，但在中频嵌入水印不能起到很好的不可见性，图像信息丢失，所以中频不宜嵌入水印，而且该算法对嵌入强度有一定的限制．

本文提出了一种非采样Contourlet变换与SVD结合的数字水印算法，先对图像进行非采样Contourlet变换，然后对变换后的低频子带进行奇异值分解．因为大部分的能量集中到低频子带上，若对图像进行信号处理，对低频子带的影响较小，而且低频子带能够满足人们视觉质量的要求，所以在低频子带上嵌入水印可满足水印的不可见性．为了更安全起见，将水印进行置乱预处理后嵌入到奇异值中，利用奇异值的稳定性，确保了算法的鲁棒性，通过实验证明该算法不但对常见的攻击有很好的鲁棒性，同时提高了抗几何攻击能力．

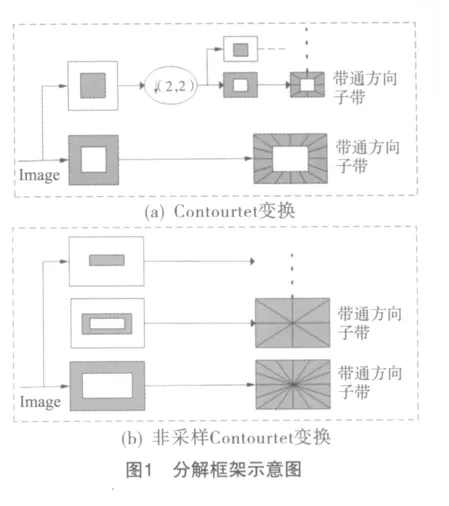
1 非采样Contourlet变换

1．1 非采样Contourlet变换

非采样Contourlet变换具有Contourlet变换没有的平移不变性．同Contourlet变换相似，非采样Contourlet变换先用非采样塔式滤波器组(Nonsubsampled Pyramid Filter Bank)来进行多尺度分解，将图像分解为低频和高频，再用非采样方向滤波器组(Nonsubsampled Directional Filter Bank)对高频子带进行多方向分解，把同方向上的奇异值汇集为一个系数，但非采样塔式滤波器组与Contourlet变换中的拉普拉斯金字塔，非采样方向滤波器组与Contourlet变换中的方向滤波器组均不同，它们都不存在下采样的过程，满足平移不变性．图1为非采样Contourlet变换和Contourlet变换分解框架示意图．

在非采样Contourlet变换中，可以将图像分解为与原图像相同大小的子带图像，而在Contourlet变换中则不同，子带图像大小与分解的层数和方向数有关，且非采样Contourlet变换避免了频谱泄露和丢失方向子带的位置信息．

1．2 奇异值分解(SVD)在水印算法中的应用

SVD是线性代数的重要工具之一，表征的是图像内部的性质，矩阵奇异值的定义为：

设 Am×n是 m × n 的矩阵，则存在酉矩阵 Um×n和 Vm×n，使得：

其中，D=diag(d1，d2，…，dr)，且 d1≥d2≥…≥dr≥0，di(i=1，2，…，r)称为矩阵 A 的奇异值，r为 D 的秩．

奇异值分解(SVD)在数字信号处理等领域有广泛的应用前景，在数字水印算法中主要应用是：

1)奇异值具有一定的稳定性，即在奇异值上嵌入水印后若对其进行微小的操作处理则不会有很大的改变［3］．

2)奇异值具有几何不变性［7］，则几何变形有：旋转、转置、镜像等．

①旋转：图像A与任意角度旋转后的图像Ar有相同的非零奇异值，即水印具有旋转不变性．

②转置：图像A与它的转置AT有相同的非零奇异值，即水印对转置变形是稳定的．

③镜像：图像A与它的行镜像Arn和列镜像Acn有相同的非零奇异值，即水印对镜像变形是稳定的．

2 水印的嵌入及提取

2．1 本文算法的设计思想

本文将非采样Contourlet变换和SVD相结合，根据非采样Contourlet变换的特性和SVD在水印算法中应用到的特性，设计了对非采样Contourlet变换后的低频子带进行奇异值分解，在奇异值上嵌入水印信息，由于奇异值具有一定的稳定性，对水印来说，这保证了水印的鲁棒性，又因为奇异值具有旋转不变性、非采样Contourlet变换不仅具有多分辨率和时频性，而且具有多方向性、各向异性和平移不变性，因此本算法能较好地在保证不可见性和鲁棒性前提下，提高水印的抗几何攻击性，同时也避免频谱泄露、子带的方向信息丢失等问题．

在本文算法中，采用Arnold变换置乱预处理变换确保水印信息的安全，进一步提高水印的不可见性和算法的鲁棒性．Arnold变换置乱的目的是把遭到损坏的原先集中在一起的图像像素分散开来，通过减小对人视觉的影响来提高数字水印的鲁棒性．Arnold变换具有周期性，即若继续对置乱后的图像进行迭代，将在后面的某一步将原始图像恢复．

2．2 水印嵌入算法

1)读取水印图像，对水印图像进行k次Arnold变换，k为密钥;

2)读取原始图像，对图像进行3层非采样Contourlet变换，得到低频子带和一组高频子带;

3)对低频子带矩阵A进行奇异值分解：A=USVT;

4)将置乱的水印信息W迭加到S上得到S'：S'=S+aW;

5)将嵌入水印的奇异值矩阵S'进行分解：S'=U1S1VT1，将S'恢复到子带中替代原来的S，与对应的酉矩阵重构低频子带;

6)对低频子带与各带通子带进行非采样Contourlet变换反变换，得到嵌入水印后图像．

2．3 水印提取算法

1)对含水印的图像进行与上相同的3层非采样Contourlet变换，提取低频子带;

4)提取奇异值与嵌入水印前的奇异值相减得到水印信号：W'=(D'－S)/α;

5)对水印信号进行T－k次Arnold变换，提取水印．

3 仿真实验

本文实验采用512×512像素的Lena灰度图像作为原始图像，64×64像素的“雨花校区”组成的二值图像作为原水印图像，在Matlab 7．0上进行仿真实验，使用相关系数NC来检测原始水印图像和恢复的水印图像之间的相似程度，见公式(2)，并将本文算法与基于DWT－SVD和Contourlet－SVD的同种嵌入规则的水印算法进行比较分析．

3．1 算法实验结果与分析

本文对水印图像进行置乱预处理后嵌入到图像中，使水印信息更安全，有更好的不可见性，如图2(d)经过5次Arnold置乱后的水印图像．从图2(b)可看出嵌入水印后的图像失真很小，从视觉上看没有任何变化，图像在微小变化后质量没有受到影响，而且恢复的水印图像与原始图像从视觉上无任何差别，提取的水印图像质量也很好，如图2(e)，其中NC=1．本算法由于采用非采样Contourlet变换，对嵌入强度几乎没有限制，在嵌入强度增加的情况下，仍能保证水印的不可见性，因此该算法很好地满足了水印的不可见性和鲁棒性．

3．2 算法的攻击测试

为了更好地说明本算法的鲁棒性，本文对图像进行各种攻击试验，如图3所示，嵌入水印后的图像受到椒盐噪声、高斯噪声、剪切、JPEG压缩及旋转和高斯滤波攻击后的图像．

表1给出了本文算法抵抗各种常规攻击测试后的部分数据结果，从数据结果可以看出本文算法对常规的攻击具有很好的鲁棒性，而且更能有效地抵抗几何攻击，如旋转、剪切几何攻击等．

表1 本文算法鲁棒性测试

3．3 算法的性能比较分析

表2给出了本文算法与在相同嵌入规则下基于DWT－SVD水印算法和基于Contourlet－SVD水印算法的攻击测试比较表．

表2 本文算法与DWT－SVD和Contourlet－SVD算法攻击测试比较表

从表1、2中的实验数据可看出对于常见的攻击，本文算法提取出的水印与原始水印图像相似程度最高．DWT－SVD算法受到JPEG压缩80%、中值滤波、高斯滤波攻击后提取出的水印质量较好;Contourlet－SVD算法受到椒盐噪声、高斯噪声和JPEG压缩攻击后提取出的水印质量较好，对抗常见攻击的鲁棒性比基于DWT－SVD算法的有所提高;DWT－SVD算法、Contourlet－SVD算法受到旋转几何攻击后提取出的水印质量明显下降，而非采样Contourlet－SVD算法仍能提取出很好的水印，且对抗JPEG压缩、中值滤波和高斯滤波攻击的鲁棒性也有所提高，由此可见，本文提出的算法进一步提高了对抗常见攻击的鲁棒性和抗旋转几何攻击的能力．

本文算法的实验结果与文献［5－6］相比，提高了对抗JPEG压缩、中值滤波、高斯滤波和旋转攻击的能力，具有更好的鲁棒性．

4 结语

本文提出了一种基于非采样Contourlet变换和SVD结合的数字水印算法，对图像进行非采样Contourlet变换后，提取低频子带，对低频子带进行奇异值分解，利用SVD的稳定性在奇异值上嵌入水印，该算法的主要特点有：

1)由于非采样Contourlet变换具有多分辨率、时频局部性及多方向性、各向异性和平移不变性，能够更准确地提取和捕捉图像几何特性，避免Contourlet变换的频谱泄露、子带的方向信息丢失等问题，又因为非采样Contourlet变换是高冗余度的Contourlet变换，所以基于非采样Contourlet变换的水印算法嵌入的信息量更大、嵌入点的选择范围大且具有更好的鲁棒性．

2)水印嵌入到非采样Contourlet变换的低频，嵌入强度可比其他算法的嵌入强度高，且仍不影响算法的不可见性．

通过实验结果表明，本文算法在满足不可见性的同时，对常见的攻击有很好的鲁棒性，且提高了对抗JPEG压缩、中值滤波、高斯滤波和旋转攻击的能力．

［1］ DO M N，VETTERLI M．Contourlet：a directional multiresolution image representation［C］//Conference Record of the Thirty－Sixth Asilomar Conference on Signals，Systems and Computers．Pacific Grove：IEEE，497 －501．

［2］ DO M N，VETTERLI M．The contourlet transform：an efficient directional multiresolution image representation［J］．IEEE Trans on Image Processing，2005，14(12)：2 091 －2 106．

［3］ ZHOU Jianping，CUNHA A L，DO M N．Nonsubsampled contourlet transform：construction and application in enhancement［C］//ICIP 2005．Genoa ：IEEE International Conference on Image Processing，469 －472．

［4］ CUNHA A L，ZHOU Jianping，DO M N．The nonsubsampled contourlet transform：theory，design，and applications［J］．IEEE Trans Image Processing，2006，15(10)：3 089 －3 101．

［5］曾凡娟，周安民．基于Contourlet变换和奇异值分解的图像零水印算法［J］．计算机应用，2008，28(8)：2 033－2 035．

［6］顾国生，何元烈．一种Contourlet域图像鲁棒水印算法［J］．计算机工程与应用，2010，46(14)：179－211．

［7］叶建兵．一类SVD水印算法的问题分析及Contourlet域的水印嵌入与检测算法［D］．南京：南京理工大学，2007．

［8］王建平，吕述望．应用Contourlet的具有抗几何攻击能力的水印算法［J］．传感技术学报，2009，22(6)：883－886．

［9］朱香卫，肖亮，吴慧中．Contourlet与小波域鲁棒性水印算法性能比较［J］．计算机工程与应用，2009，45(9)：120－145．

［10］刘乃成，周枫．一种基于DWT和DCT的彩色图像半脆弱水印算法［J］．云南民族大学学报：自然科学版，2009，18(4)：368－371．

［11］ XU C，PR J L．Snake，shapes，and gradient vector flow［J］．IEEE Transaction on Image Proccssing，1998，7(3)：359 －369．

［12］刘晶，刘刚，李爱民，等．基于非采样Contourlet特征的水印算法［J］．计算机工程，2009，35(17)：142－145．