基于复杂网络的多级混沌保密通信系统的研究

付宏睿，俞建宁，张建刚

(兰州交通大学数理与软件工程学院，甘肃兰州730070)

自从1990年Pecora和Carroll［1］首次发现混沌同步以后，混沌同步得到各个领域的普遍关注并掀起了研究热潮［2－4］．在复杂动力学网络中，一个重要的现象就是节点之间的同步．如果复杂网络中各个节点代表一个混沌系统，那么复杂网络的同步就是大量节点的混沌同步问题［5－9］．

由于混沌信号本身具有良好的特性，所以非常有利于应用在保密通信系统中［10－13］．混沌信号自身具有非周期性连续带宽频谱，类似噪声及对初值极端的敏感性，使得它具有不可预测和天然的隐蔽性，利用上述特点将其应用于保密通信．信号的混沌加密主要是信号的加密，解密以及信号的传输．混沌加密的方式多种多样，但是目前大多数复杂网络的混沌通信系统都是含有2个节点的混沌系统，在发送端经过1次加密，在接收端解密1次就可以恢复有用信号，安全性比较低．本文利用对初值极其敏感的多节点的混沌系统对信息进行加密，多节点的混沌保密通信系统含有3个或更多个节点的混沌系统，可以大大提高混沌保密通信的安全性．

本文对复杂网络中具有N个节点的全局耦合网络的全局渐近同步进行了研究，给出了其同步的条件，并将其应用到保密通信中，提出了一种多级混沌保密通信系统的实现方法．最后对3个节点的Lorenz系统的全局耦合网络进行了数值仿真，证明了该方法的有效性．

1 模型描述

1．1 复杂网络模型

考虑一个由N个相同节点通过耦合作用构成的网络，在这个网络中每个节点都是一个n维的动力系统．网络中第i个节点的状态方程为：

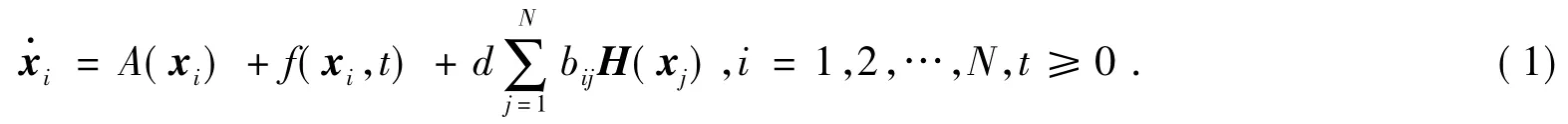
其中A(xi)+f(xi，t)表示节点间无耦合作用时的混沌系统，xi=(xi1，xi2，…，xin)∈Rn为节点i的状态变量，常数d为耦合强度，H(xj)：Rn→Rn为各个节点状态变量之间的内部耦合函数，也称为各节点的输出函数，假设每个节点具有相同的输出函数，矩阵B=(bij)N×N表示网络的耦合矩阵，当耦合矩阵B描述了一个无权无向拓扑网络时，其定义如下：当i≠j时，若节点i和节点j之间有连接，则bij=1;若节点i和节点j之间不存在连接，则是一个对称矩阵．

1．2 复杂网络同步的定义

2 混沌同步方案

2．1 理论分析

考虑由N个相同节点组成的全局耦合网络，这N个相同节点构成的全局耦合网络模型如式(1)．全局耦合网络的连接矩阵为：

并令各节点的状态变量之间的内部耦合函数为：

则N个相同节点的全局耦合网络模型为：

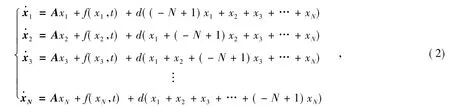
设

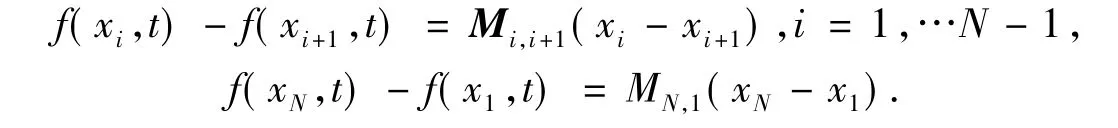
由于混沌系统的状态轨迹都是有界的，而Mi，i+1(i=1，…，N-1)，MN，1都是关于状态轨迹的函数矩阵，故都为有界矩阵．令各个节点的同步误差为：

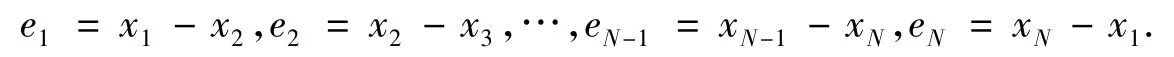
则误差系统为：

所以误差系统写成向量形式为：

其中，D=diag(d，d，…，d)n，n 是节点的状态变量个数．

定理1 若存在耦合强度d＞0，使得BN+BTN对于x1，x2，…，xN(由于混沌是有界的，即x1，x2，…，xN有界)一致负定，则误差系统(3)的零解一致渐近稳定，从而全局耦合网络(2)全局渐近同步．其中：

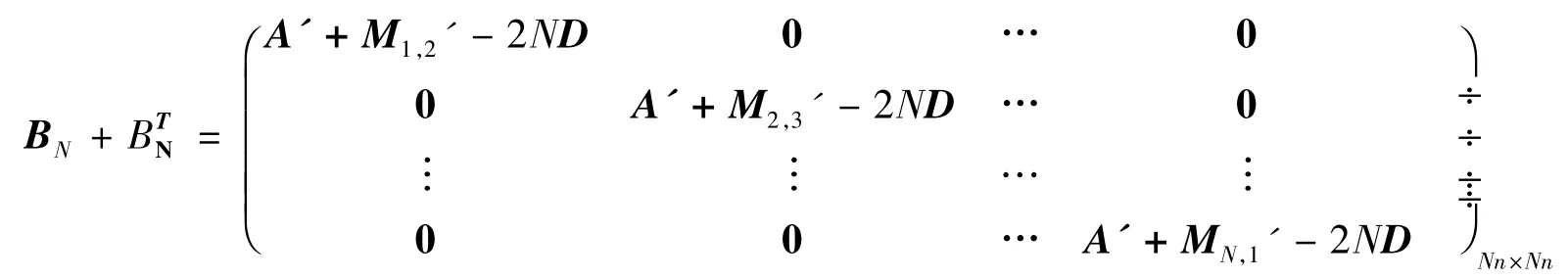
其中，A'=A+AT，Mi，i+1'=Mi，i+1+MT

i，i+1，i=1，2，…，N-1，MN，1'=MN，1+MT

证明 构造Lyapunov函数为：V=eTe则V延误差系统(3)的解的全导数为：

N，1．

2．2 数值仿真

以Lorenz系统为网络节点，取节点数N=3，Lorenz系统为：

因为网络中的节点是相互耦合的，故3个节点的全局耦合网络模型为：

运用Matlab进行数值仿真，选取耦合参数d=2，仿真结果表明3个节点的初始状态不同，但最终实现了混沌同步．同步误差图如图1所示．

3 复杂网络节点间的保密通信

为了提高复杂网络节点之间的混沌同步保密通信系统的安全性能与传输性能，提出了如图2所示的复杂网络的多级混沌同步保密通信系统．在发送端，有用信号首先与混沌信号进行合成，将合成的混沌信号作用于第1个节点的混沌系统，然后将传输的混合信号

在作用于第2个节点的混沌系统;在接收端，发送系统与接收系统同步以后，经信道传输的混沌信号经过2级解调后恢复出原有用信号．显然，由于有用信号直接作用于混沌系统且经过多次加密，并且在接收端必须经过2级解调才能恢复有用信号，考虑到混沌信号对初值的依赖性与敏感性，故该方案在安全性能方面要优越于以往的同步掩盖保密方案．

选择连续信号m(t)=sin(t)，混合信号为s(t)=m(t)+x11(t)，由图2可知：s'(t)=s(t)+x21(t)，s″(t)=s'(t)+x31(t)．设m'(t)和m″(t)分别是第1次和第2次解密后的信号．令节点1和节点2为发射系统：

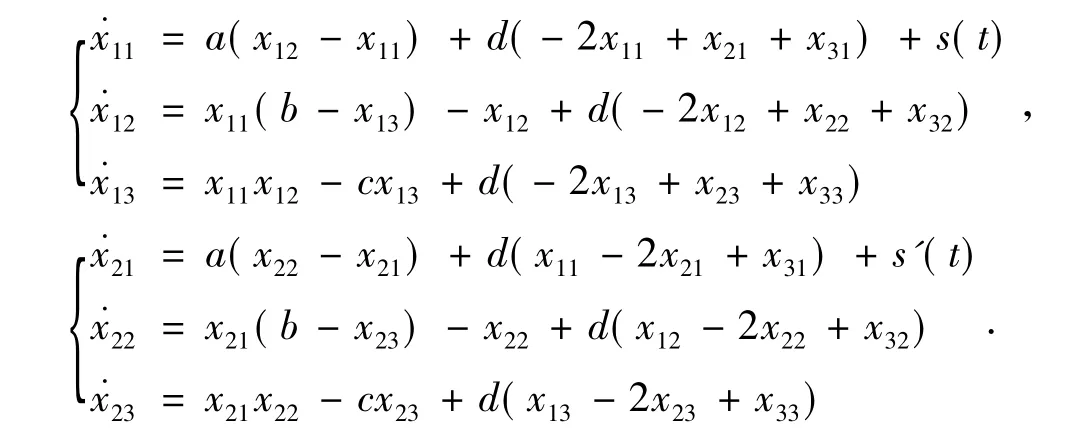
令节点3为接收系统：

图3显示了数值仿真结果．很明显，有用信号很快恢复出来．这种基于3个节点的混沌系统的多级混沌同步保密通信系统经过了2次加密，与以往的2个节点的混沌系统同步加密相比有更高的安全性．

4 结语

本文对具有N个节点的全局耦合网络进行了研究，根据Lyapunov稳定性理论，得到了节点全局渐近同步的条件，使网络能快速的达到同步．提出了一种基于多个节点的多级混沌保密通信系统，并且进行了数值仿真，仿真结果表明本系统很好的实现了保密通信．验证了结论的可靠性．

［1］ PECORA L M，CARROLL T L．Synchronization in chaotic systems［J］．Phys Rev Lett，1990，64(8)：821 － 824．

［2］ CARROLL T L，PECORA L M．Synchronization chaotic circuits［J］．IEEE Trans Circuits and Systems，1991，38(4)：453 －456．

［3］ LIAO Xiaoxin，CHEN Guanrong．On global synchronization of chaotic systems［J］．Dynamics of Continuous，Discrete and Impulsive Systems，2003，10：865 －872．

［4］朱清祥，张蕊．陈氏混沌系统的混沌同步［J］．武汉理工大学学报，2008，30(3)：348－358．

［5］ ZHANG Rong，HU Manfeng，XU Zhenyuan．Synchronization in complex networks with adaptive Coupling［J］．Physics Letters A，2007，368(8)：276 －280．

［6］ ZHOU Jin，LU Junan，LU Jinhu．Pinning adaptive synchronization of a general complex dynamical network［J］．Automatica，2008，44(4)：996 －1003．

［7］胡爱花，徐振源，李芳．复杂网络连接的Chen系统的同步化［J］．系统科学与数学，2007，27(2)：302－313．

［8］赵永清，江明辉．基于复杂网络的混沌同步研究［J］．三峡大学学报：自然科学版，2009，31(6)：67－72．

［9］吕翎，张超．一类节点结构互异的复杂网络的混沌同步［J］．物理学报，2009，58(3)：1462－1465．

［10］王瑞兵，姚洪兴．复杂网络的同步及保密通信［J］．微计算机信息，2007，23(3)：103－104．

［11］龚美静，瞿少成，王晓燕．一种通过异结构同步实现混沌保密通信新方法［J］．电子与信息学报，2009，31(6)：1 442－1 444．

［12］王晓燕，瞿少成，田文汇．异结构混沌系统同步及其在保密通信中的应用［J］．计算机应用研究，2009，26(5)：1 874－1 876．

［13］ AN Xinlei，YU Jianning，ZHANG Jiangang，et al．A new multistage chaos synchronized system for secure communications［C］//2009 Fifth International Conference on Natural Computation．Washington DC：IEEE Computer Society，2009，437 －441．

［14］马知恩，周义仓．常微分方程定性与稳定性方法［M］．北京：科学出版社，2001：70－71．