目标区域下汇率扩散模型的统计分析

曹玲玲

(江苏宿迁学院经济贸易系，江苏宿迁223800)

汇率制度的问题一直倍受许多学者的关注，其中最为重要的就是汇率目标区域的提出．最早提出这一汇率改革举措的是荷兰财政大臣Duilsenbery．此后，美国学者Williamson和Bergsten［1］提出了详细的汇率目标区设想及行动计划．建立汇率目标区模型的任务最终是由Paul Krugman［2］完成的．他在《汇率目标区和汇率动态》和《有限储备下的汇率目标区》中提出了汇率目标区的规范理论模型．我国学者王国青［3］指出，虽然我国并未宣布建立人民币汇率的目标区域，但其作法与目标区域汇率制度下的汇率安排已具有某些相似性．这为使用目标区域模型来分析人民币汇率的变动提供了实践上的依据．魏巍贤［4－5］运用所建立的模型对1997年4月至9月的人民币汇率走势进行预测．

随着Cox，Ingersoll，Ross［6］利率期限结构模型的发展和目标区域理论的不断完善，一些学者也将利率期限结构模型的思想应用于汇率模型当中，即假设汇率的对数变动是一个平方根过程．我们将Frank，Drost，Werker［7］给出的目标区域里的汇率的扩散模型记为FDW模型，模型满足：其中Xt是汇率的对数，m为中心汇率的对数，Z=ln(1+z)且 z是汇率波动的幅度，扩散系数 σ保证了汇率是在目标区域下运行的．

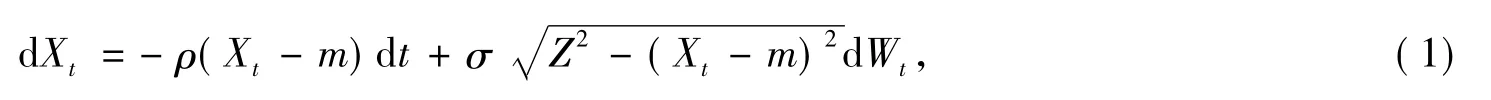
Larsen和Sorensen［8］在上述模型的基础上引入了2种汇率之间的相关系数γ，允许货币之间的不对称，将这种模型命名为KS模型．模型满足：

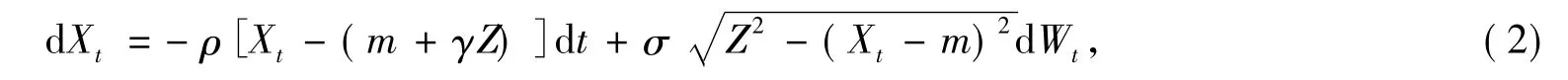
其中γ∈(－1，1)表示2种货币的相关程度．

关于模型的估计问题，陈萍等［9］利用条件矩法对Cox，Ingersoll，Ross的模型进行了估计．Frank，Drost和Werker［7］分别用拟极大似然估计和GMM方法对FDW模型进行了估计，并验证了该模型适用于欧洲货币体系的货币．Larsen和Sorensen利用特征函数的估计方法［7－8］得出KS模型参数的估计量．本文统一采用GMM方法对FDW模型及KS模型进行参数估计，并通过实证比较2种模型对人民币汇率的拟合效果．

1 模型的统计特征

1)考虑模型(1)，其中m为中心汇率的对数，中心汇率是由中央政府确定的，一定时期内中心汇率是固定不变的，且ρ＞0，Z ＞0，σ ＞0．当Xt＞m时，漂移项是负的，那么Xt就有向下运动的趋势;当Xt＜m的时候，漂移项就是正的，那么Xt就有向上运动的趋势;而当Xt=m的时候，漂移项为0，说明Xt具有保持不变的趋势．这就体现了汇率的对数具有均值回复的特征．ρ代表均值回复的速度，ρ越大，那么Xt在偏离中心汇率的对数m后的回复速度就越快．而扩散系数保证了汇率的对数是在目标区域下运行的．当Xt＜m时，波动率是Xt的增函数，当Xt＞m的时候，波动率又是Xt的减函数，这说明该过程是一个对称的过程．并且当汇率的对数Xt运行达到边界m±Z的时候，扩散项就为0，漂移项又会使得汇率重新回到中心汇率的水平．

引理1［7］设Xt服从(1)，记Yt=Xt－m，则方程变为：

dYt=－，则在市场概率测度下，对给定的Yt，Yt+h的条件期望、方差分别为：

2)考虑模型(2)，其他参数和上模型相同，只是在该模型中加入了2种货币的相关系数γ∈(－1，1)．且汇率的对数的长期水平不再是中心汇率的对数m，而是m+γZ．

定理1 设Xt服从(3)，记Yt=Xt－m，从而方程变为：

则在市场概率测度下，对给定的Yt，Yt+h的条件期望、方差和三阶中心矩分别为：

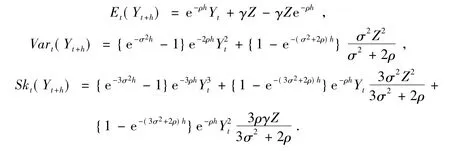
2 模型的GMM

一般地，GMM 方法就是使得矩条件 E［qt－1mt(β)］=0 通过极小化目标函数 Q(β)=m(β)'W－1m(β)，其中权重矩阵W为某正定矩阵，qt－1是工具变量．

1996年Meddahi和Renault［10］给出了条件异方差模型下的广义矩估计方法的理论．在该理论中他们选取的矩向量为残差矩向量．为了得到参数β的表达式，只要得出矩条件E［qt－1mt(β)］=0的表达式就可以，从而离散形式就变成

Godambe［11］给出了残差矩向量对应的最优的工具变量qt－1的值，即为

其中Vart－1是协方差矩阵．

根据引理我们可以看出选定的2种模型中汇率对数的离散观察值满足AR(1)－ARCH(1)模型，以模型(1)说明：

其中 ρh=e－ρh＜ 1 αh={e－σ2h－ 1}e－2ρh＜ 0，ωh=

下面根据(4)和(5)构造参数的估计函数

记 μt=Et－1(Yt)，ht=Vart－1(Yt)，st=Et－1(Yt－ μt)3，令εt=Yt－ μt，我们采用三阶矩条件进行估计，此时残差向量：

协方差矩阵为：

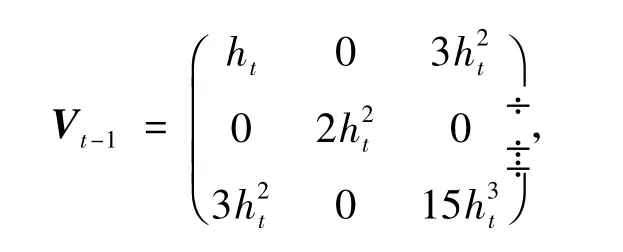
工具变量为：

表1 汇率的对数及其一阶差分的描述性统计

所以参数满足的估计方程就是：

3 实证分析

首先我们研究的是目标区域下的汇率扩散模型，因而在选取的数据中要确保汇率不会超出边界．其次，根据很多学者关于目标区域下汇率模型的研究知道，中国在实行汇率目标区的时候，汇率的波动幅度一般选为2% ～3%．并且结合实际情况，中心汇率在比较长的时期并不是一成不变的，这就要求我们在选择数据的时候，数据期间跨度不能很大．因此在本文中选取的2006年一整年的汇率数据，经检验后没有超出目标区域的数值．

样本为2008年人民币兑美元的中间报价，共计243个样本数据．由于我们的模型中基础变量是汇率的对数，因而我们首先对汇率取自然对数，其中为计算方便，将汇率扩大100倍．下面就对人民币兑换美元的汇率的对数做统计分析(见表1)．

根据上面的结果我们可以看出，汇率对数的标准差是0.009 239，说明汇率的波动不是很大，这样就能保证汇率能在目标区域下运行．而偏度小于0，说明分布呈现左偏态，并且峰度小于3，则说明汇率的对数是在均值周围，并没有出现远离均值的数据出现．同时Jarque－Bera检验说明汇率的对数及其一阶差分不是服从正态分布的．

下面我们利用GMM方法进行参数估计，由上面的分析，我们知道汇率的对数满足AR(1)－ARCH(1)模型，因而我们首先验证所选取的数据是否符合，见图1．离散点是我们的实际观察值．从拟合的效果可以看出，我们选取的数据满足AR(1)－ARCH(1)模型．下面我们就要根据我们所选取的数据，对2种模型进行参数估计．

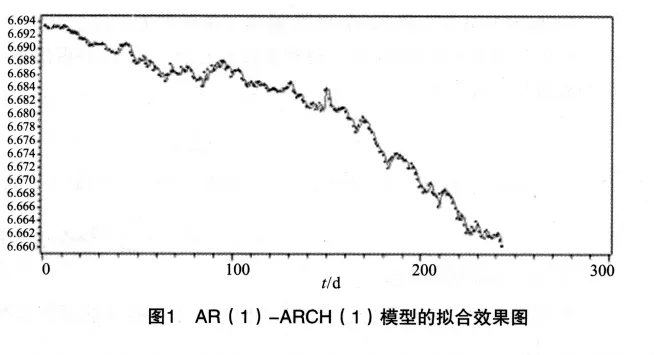
FDW目标区域下的汇率扩散模型估计结果：

模型满足 dXt=－ρ(Xt－m)dt

关于中心汇率的选取本文采用最简单的方法，即是选取观察期内汇率的均值作为我们要选取的中心汇率，即 m=6．681 028，汇率的波动范围选为2．5%．经过检验知道，没有出现汇率超出目标区域的数值．

GMM估计结果见表2．参数 ρ

是该模型的均值回复系数，表示汇率对数回复的速度是0．094 963．波动率σ的估计结果为0．006 246．可以看出GMM方法对FDW目标区域下的汇率扩散模型估计很有效．

表2 FDW目标区域下的汇率扩散模型GMM估计结果

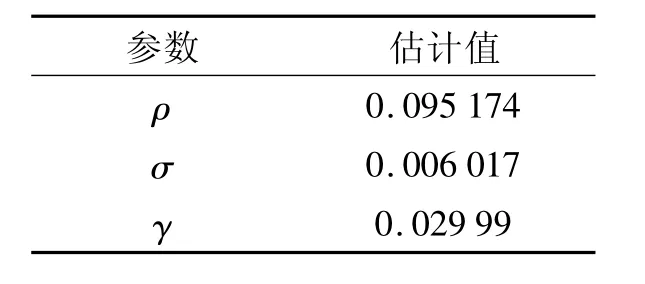
表3 KS目标区域下的汇率扩散模型GMM估计结果

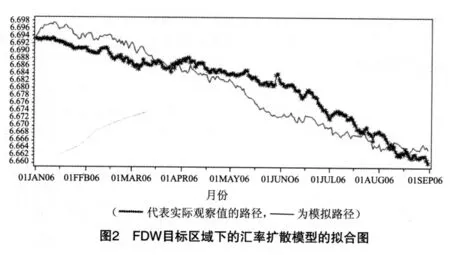
因为该扩散模型关于中心汇率是一个对称的过程，因此当汇率低于中心汇率的时候我们模拟的汇率值取值为关于中心汇率对称点，进而得到模拟效果图．

FDW目标区域下的汇率扩散模型模拟路径和观察值路径的比较见图2．

KS目标区域下的汇率扩散模型估计，同样的我们选取观察期内汇率的均值作为中心汇率，即m=6.681 028，汇率的波动范围选为2．5%．GMM估计结果见表3．

根据估计的结果我们可以看出汇率的对数的均值回复速度是0.095 174，而人民币与美元的相关系数为0．029 99，这与实际美元与人民币的相关性不符，我们知道人民币汇率是以盯住美元等一揽子货币来确定的，而在很大程度上人民币是盯住美元的，而相关系数小于0．3就是微相关，因此估计值失真．

从2种模型估计的结果可以看出，2种模型都能很好地估计出均值回复速度和波动率，但是KS模型估计出的2种货币的相关系数严重失真．从FDW模拟效果看，模型可以较好地描述短期人民币对美元的汇率波动情况．

［1］ WILLIAMSON J，BERGSTEN F．Target zone and policy coordination［J］．Washington D C Institute for International Economics，1985(11)：54 －57．

［2］ KRUGMAN P R．Target zones and exchange rate dynamics［J］．Quarterly Journal of Economics，1991，106(3)：669 －682．

［3］王国青．人民币汇率目标区域模型初探［J］．南开经济研究，1996，12(3)：50－53．

［4］魏巍贤．人民币汇率的稳定机制及其动态过程—目标区域模型［J］．系统工程理论与实践，1999，19(10)：55－62．

［5］魏巍贤．人民币汇率决定模型的实证分析［J］．系统工程理论与实践，2000，20(3)：68－77．

［6］ COX J J，INGERSOLL J E，ROSS S A．A theory of the term structure of interest rates［J］．Econometrica，1985，53(2)：385 －407．

［7］ FRANK D J，DROST F C，WERKER B J M ．A jump －diffusion model for exchange rates in a target zone［J］．Statistical Neerlandica，2001，55(3)：270 －300．

［8］ LARSEN K S，SORENSEN M．Diffusion models for exchange rate in a target zone［J］．Mathematical Finance，2007，17(2)：285 －306．

［9］ 陈萍，杨孝平．Cox－Ingersoll－Ross模型的统计推断［J］．应用概率统计，2005，21(3)：285 －292．

［10］ MEDDAHI N，RENAULT E．Linear statistical inference for ARCH－type Processes［R］．Working paper University of Toulouse，1996．

［11］ GODAMBE V P．The Foundation of finite sample estimation in stochastic processes［J］．Biometrica，1985，72：419 －428．