昆明市人口预测模型研究

龙承星，张 波

(1.湖南人文科技学院数学系，湖南娄底417000;2.云南大学数学与统计学院，云南昆明650091)

一个国家或一个地区根据人口现状以及对影响人口发展的各种因素的假设，对未来某一时间人口规模、水平和趋势所做的测算，即为人口预测．如何使人口、资源、环境与经济协调发展已经成为当今社会众多学者关注的问题．然而，人口预测是一个比较复杂的问题．因为影响人口发展过程的因素很多，要将这些所有因素都准确地包含在预测之内，显然是比较困难的．所以在人口预测中，一般只能根据过去的人口发展变化的实际统计资料，加以分析比较，找出历史上人口发展过程中一些带有共同规律并考虑到未来其他各种因素的影响．

1 昆明市人口现状描述与分析［1］

根据2000年第5次全国人口普查，昆明市常住人口578万1 294人，男性人口303万9 862人，占总人口的52.581%，女性人口274万1 432人，占总人口的47.419%，男女性别比例是110.885 9∶100．与1990年相比，这10年间昆明市共增人口54万2 200人，平均每年增长人口5万4 220人．从1949～2000年昆明市人口总数以及自然增长率来看，其总人口一直是处于增长状态，并且其环比增长率除了1967年下跌以外，也是呈上升的趋势，特别是改革开放以来，环比增长率更是快速提高．从育龄妇女生育率来看，生育高峰人群为20～34岁之间的育龄妇女，特别是20～29岁的育龄妇女，生育率更是高，几乎在8%以上．调查中我们发现，昆明市婴儿死亡率高达0.529 7%，之后，随着年龄的增长，死亡率有所下降，但是25岁以后死亡率又陆续攀升，特别是65～69岁的人口死亡率高达2.066 2%．从分性别死亡率来看，除了男性0～4岁婴儿的死亡率低于女性，其他的年龄段男性的死亡率均高于女性．昆明市性别结构基本正常，但是5～9岁、20～44岁、50～54岁、60～64岁的性别结构已经超过了107的国际警戒线，处于成年型向老年型转变的阶段．全市少儿抚养比比较高，从而导致了全市总抚养比也比较高．所以，昆明市的年龄结构以及由此引起的抚养系数表现出较强的不适应性，年龄结构已经从成年型向老年型过渡，而少儿抚养比仍然很高．

2 人口预测模型及合理性

2．1 马尔萨斯人口模型［2］

假设在t时刻(单位以年计)人口为P(t)，则人口的增长率由出生率B(p，t)和死亡率D(p，t)决定．假定 B(p，t)和 D(p，t)不随时间的变化而变化，即相对于 t来说，B(p，t)和 D(p，t)为常数，从而有B(p，t)=B(p)，D(p，t)=D(p)．如果说1 000人中每年有50个小孩出生，那么我们认为2 000个人中每年有100个小孩出生是有道理的．换句话说就是出生率与人口成正比的．如果我们设出生率为R1，死亡率为R2，则有B(p，t)=B(p)=R1P(t)，同样道理，D(p，t)=D(p)=R2P(t)．此处 R1和 R2为大于 0 的常数，并且一般来说R1－R2＞0．

由上面的叙述可以得出：

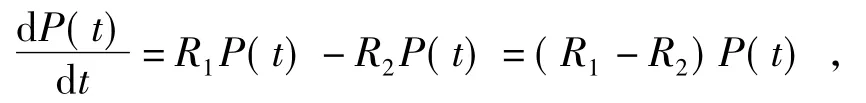
令 R1－R2=α，则

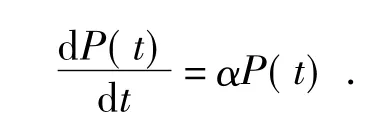
假设在基年t0时的人口数量是P(t0)，则我们对进行积分，可以解出

P(t)=P(t0)eα(t－t0)，这即是大家熟知的马尔萨斯人口模型．

但是，自然增长率α不是一个固定不变的值，在应用这个模型的时候我们还得对昆明市的人口自然增长率进行估计．

通过昆明市1981～2000年人口自然增长率，我们作出自然增长率如图1所示．

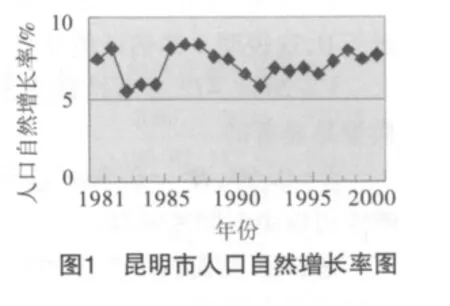
我们可以看出，昆明市的人口自然增长率并不是一直上升的，而是有上下起伏波动的．此时我们就要用时间序列模型来模拟自然增长率的趋势．若令X1代表1981年昆明市的人口自然增长率，X2代表1982年昆明市的人口自然增长率，X3代表1983年昆明市的人口自然增长率，依次类推．得到线性回归模型：

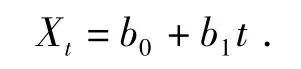
用SPSS软件［6］进行处理得到以下结果：

这说明模型是不显著的，所以这个模型不可用，我们必须寻找其它的模型．从图中我们可以看出，自然增长率随着时间的变化又不太明显的周期s=5，所以我们用多元线性回归模型［3］：

其中 t=1，2，3，…，20，b、b0、b1、b2、b3、b4、b5是待估参数，dk，t是哑元，满足

上述模型的设计使得第k年数具有相同的斜率bk．由于模型中的参数过多，使得设计矩阵不满秩．为了克服这个问题，取b=0，得到以下的模型：

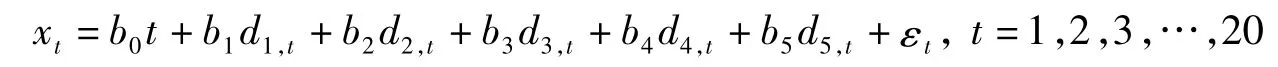
定义：

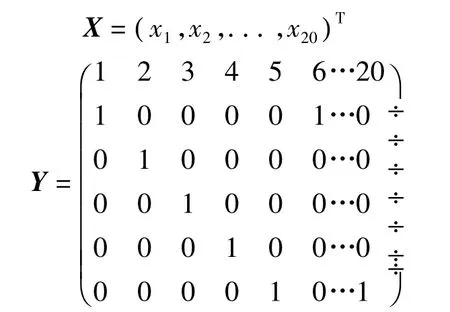
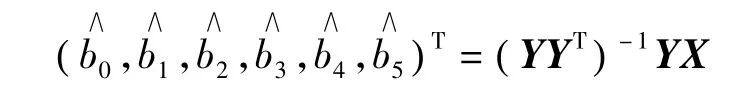
经计算可以得到回归方程：

xt=0.0227t+6.9569d1，t+7.1492d2，t+6.9589d3，t+6.6362d4，t+6.7110d5，t，从而我们可以计算 2001 ～ 2005年的自然增长率(见表1)，并与实际值之间进行比较．

从上面我们可以计算上述模型的平均误差是0.438，这个误差是很小的，这说明用这个时间序列模型来估计自然增长率是合适的．

表1 2001～2005年自然增长率预测值与实际值及误差‰

2．2 回归模型

我们用t代表年份，如1949年我们用t=1表示，依次类推;我们用yi表示第i年的人口，所以我们有以下的模型：

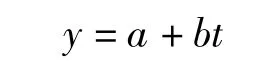
用SPSS模拟得到预测系数和方差分析结果(见表2～3)．从表2、表3中我们可以得到模型为

y=214．998+6．43t，

a=214．998，T 值等于 0．569 显著性概率 Sig接近于0，这说明a的估计值是显著异于0．

b=6．43，T 值等于45．754 显著性概率 Sig接近于0，这说明b的估计值是显著异于0．

F=2093．472显著性概率Sig接近于0，这说明模型是显著的．

R=0．99，R2=0．981 这说明昆明市人口的99%可以由时间来解释．

总体来说我们用简单回归模型来模拟昆明市人口还是合理的．

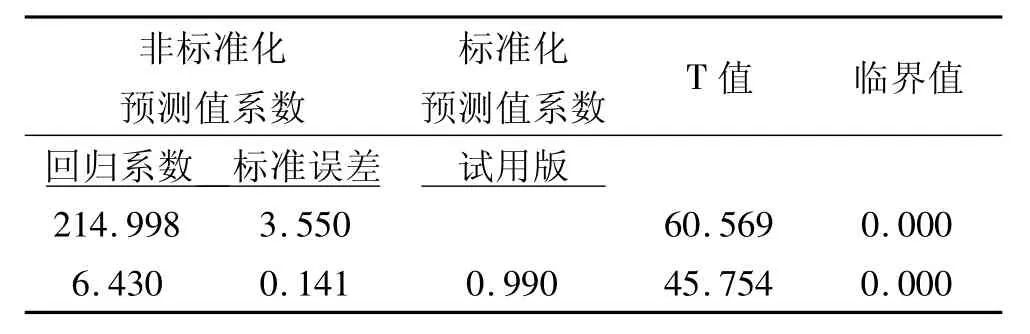
表2 预测值导数表

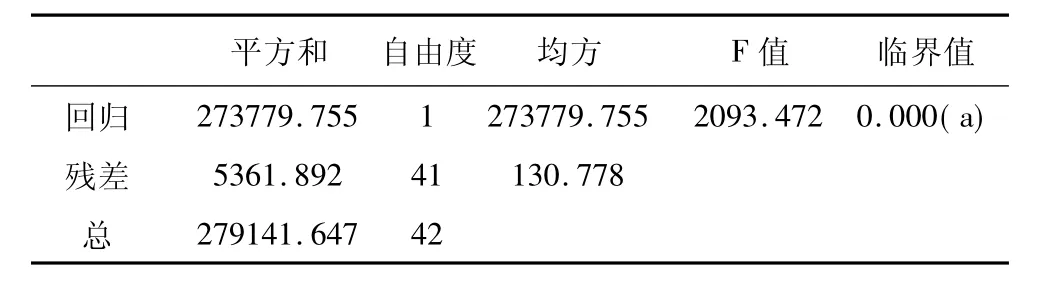
表3 模型方差分析结果

2．3 Logistic 模型［4］

英国经济学家马尔萨斯在担任牧师期间，根据统计资料，于1798年发表了《人口原理》一书，提出了著名的马尔萨斯人口模型，这个我们在前面已经介绍，但是这个模型没有反映出环境所提供的条件是不能无限制的满足人类的需要的，由于环境的限制，使得个体之间存在竞争，从而使得人口增长率α下降，荷兰生物数学家Verhulst提出增加添加项：－R1P2(R1＞0)，将马尔萨斯人口模型改进为Logistic模型：

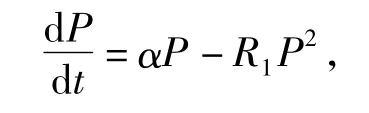
从而可以解得：

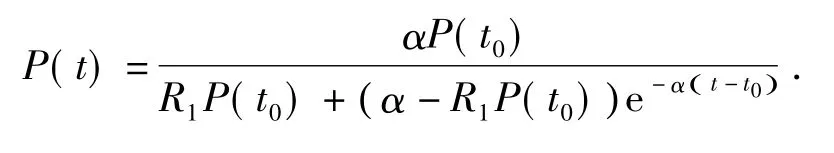
如同马尔萨斯人口模型，该模型中也存在一个出生率的确定问题，一种方法是用1981～2000年的出生率的总平均来计算，但是这种方法是不确切的．由计算可以得出1981～2000年的出生率的均值为12．743．

3 预测及模型比较

3．1 预测结果

对昆明市总人口做马尔萨斯模型、回归模型、Logistic模型预测结果，见表4～6．

表4 昆明市总人口马尔萨斯预测

表5 昆明市总人口回归模型预测

表6 昆明市总人口Logistic模型预测

3．2 模型评价

我们可以容易计算出，马尔萨斯人口模型的平均误差是最小的，为5．222，而线性回规模型的平均误差是64．81，Logistic模型的平均误差是83．68．这就说明用马尔萨斯人口模型来估计昆明市未来10年的人口数量是3个模型中最合适的．但是马尔萨斯人口模型忽略了环境、竞争等客观存在的影响人口增长的因素，这个模型预测短期内的人口是可行的，但是如果我们要预测长期的人口模型就不能用这个模型．

表5 昆明市未来十年人口的环比增长率估值

4 结论

我们用马尔萨斯人口模型估计2001～2010年的人口，从而可以得出昆明市未来10年总人口的环比增长率(以1949年为基期)的估计值(见表5)．

从表5中我们可以看出环比增长率的涨幅已经不大了，这就说明昆明市未来10年的总人口虽然一直在增长，但是增长得比较缓慢，这是一个可喜的结果．从昆明市年龄构成指数上来看，昆明市老年人口在2000年占总人口数量的比重达6．56%，这很接近7%的国际标准，而老少比也已经达到34．42%，已经超过了30%的国际标准，所以我们在考虑控制人口数量的同时，还应该建立良好的社会养老保险机制，以应对即将到来的老龄化问题．

［1］2000年昆明市第五次全国人口普查资料汇编［M］．北京：中国统计出版社，2000．

［2］方亚玲．对人口模型的研究［J］．山西煤炭干部管理学报，2002(2)：41－44．

［3］杨丽霞，杨贵山，苑韶峰．数学模型在人口预测中的应用——以江苏省为例［J］．流域资源与环境，2006(3)：287－291．

［4］任运平，杨建雅．Logistic人口模型的改进［J］．运城高等专科学校学报，1999(6)：23－24．

［5］郝黎仁，樊元，郝哲欧．SPSS实用统计分析［M］．北京：水利水电出版社，2003．