基于粒子群优化算法的产学研合作创新的知识流程分析*

秦 娜，欧晓万

(中共韶关市委党校，广东 韶关 512026)

一、引言

随着全球经济一体化的快速发展，加上信息化、网络化的迅猛发展，我们进入了全新的知识经济时期，技术创新已成为企业的竞争优势源泉。技术创新也逐渐成为企业生产经营活动的中心，知识正在成为企业的主要资产。技术创新是受制于多种因素的过程，企业必须和学术科研界等其他组织进行广泛的合作，才能获得、开发和交换各种知识、信息和资源。由此产生了为促进技术创新的“产学研合作”模式，企业通过技术购买等交易方式，获得学术科研界研发的新技术、新工艺等科技成果。产学研合作创新，有力地推动了经济和社会的发展。2009年底广东药学院启动的产学研十大重点项目，就几乎涵盖医药健康产业的各个环节。韶关东南轴承有限公司与武汉理工大学合作的“轴承套圈冷辗精密成形技术研究及其产业化”项目获得省科技重大专项立项;由科技部立项韶关学院参与承担的国家“十一五”科技支撑计划重大项目子课题“钢渣重构和性能优化技术与装备”，通过专家课题组现场验收;2011年韶关市产业园区产学研合作迈出新的步伐，成立了暨南大学韶关研究院，使韶关市与暨南大学真正有了一个为实现全方位、深层次、多角度合作的平台。韶关市将借助暨南大学在生物医药方面的研究优势，助推韶关工业园生物医药科技园发展，加速研究成果转化，促进传统产业转型升级，推动新兴产业加快发展。

产学研合作创新的核心思想是通过合作与集成实现“双赢”或“多赢”的目标，在强调集体收益的基础上，实现每个成员的收益最大化［1-2］。为充分开发利用学术科研界的创新知识资源，企业的知识管理研究与应用兴起并蓬勃发展。知识管理主要由知识获取、知识共享、知识应用与知识创新等四种核心活动组成。企业向学研方获取知识就是知识管理流程中的知识获取活动，知识管理在某种程度上就是使知识流程的这些核心活动之间取得平衡。在此环境下，信息管理活动随之进入了知识管理时代，因此，对产学研合作创新中的知识流程建模与研究是十分必要的。本文针对产学研合作中的技术交流，从理论上给出知识流程框架，并对该知识流程建模，引入粒子群优化算法(Particle Swarm Optimization，PSO算法)对模型形成的邻接矩阵进行优化。

二、模型的建立及其求解

(一)建立模型

科学技术的高速发展与广泛应用为企业的发展提供了广阔的空间。科研学术界通过提供企业发展所需要的科技资源和信息技术，帮助和促进企业成长。企业方为了自身的发展，为了实现科技成果的转化，企业方的任务之一就是向学研单位购买技术服务。技术服务包括软件研发、工程设计等，都属于知识密集型产品或称服务。从需求了解开始到合同执行为止的所有业务都属于技术服务，涉及到企业和学研方的众多部门。在不影响分析结果的前提下，为简便起见，本文只分析截至企业和学研方签订采购协议的有关活动。此知识活动包括：组织调研考察、编写需求分析、项目建议、方案筛选、项目审查等七个。为了使知识流程之间的关系更容易理解，本文采用混合流程图与文本的知识流程建模方法，对该知识活动的七个流程做了流程图，如图1。

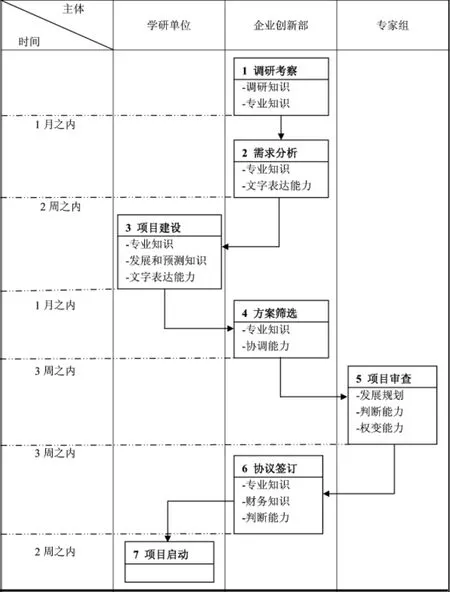
图1 企业技术采购知识流程图

利用大系统理论［3］中定性模型的方法对图1进行分析，即知识流程是以知识活动之间的相互关系作为判断标准来描述的，由图1产生的知识流程矩阵图如图2所示，利用图2产生邻接矩阵［4］，再通过邻接矩阵的变换来进行知识流程的描述。

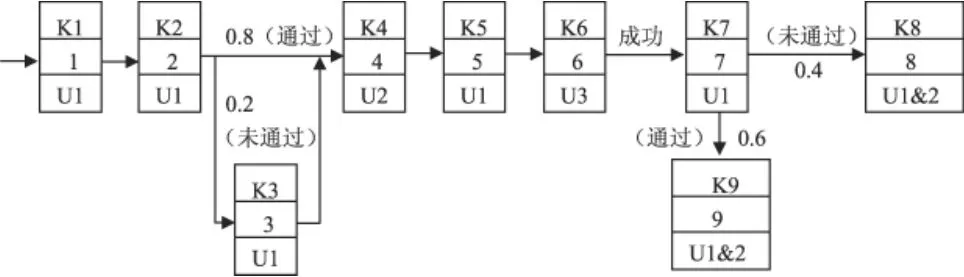
图2 企业技术采购知识流程矩阵分析

其中，Ki(i=1，2，L，9)表示第 i个知识活动所要的所有的资源总和。K1表示调研考察时所要的知识资源;K2表示专业的知识资源;K3表示相关信息资料的收集、整理和加工等;K4和K5都表示专业的知识资源;K6表示筛选和评价专业知识的方法等;K7表示签订合同的相关知识;K8表示修改合同的相关知识;K9表示发布合同的相关知识。Ut(l=1，2，3)表示相关的知识活动的主体。U1表示相关企业的部门;U2表示科研界，比如高校或科研院所等;U3表示专家组，专家组是独立于企业和学研方的。

(二)分析矩阵

需要特别说明的是，在现实生活中，是很难取得知识活动间的衔接概率的，所以图2中给出的概率只是一个估计值，这个估计值对分析效果是没有影响的。由于知识活动间的衔接概率是一个估计值，所以在矩阵分析时，相应的权重矩阵也是一个估计值。由图2可以产生邻接矩阵、可达矩阵和强联通矩阵，具体步骤如下：

1)邻接矩阵

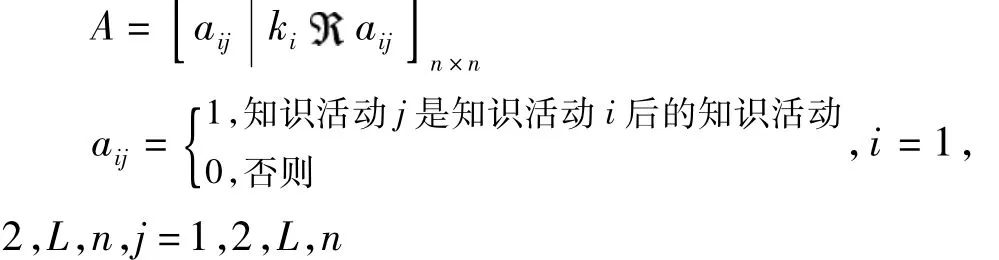
其中，矩阵A表示邻接矩阵，n表示图2的节点数目，即知识活动的个数。矩阵A中全是零的列表示起始的知识活动，全是零的行表示终止的知识活动。邻接矩阵A表示如下：

2)基于邻接矩阵A的可达矩阵R与强联通矩阵Q

可达矩阵R=(I+A)n-1，其中I表示单位矩阵，rij=1表示节点i经过若干个节点可以达到节点j，可达集表示为矩阵Q表示强联通矩阵，Q=R∩RT。如果有最大的节点D，即包含多于一个节点，使得所有的qij=1(i∈D且j∉D)，则节点集合内的所有节点构成一个知识活动环。假设一个知识活动环的节点集合为D，如果有aij=1(i∈D且j∉D)，则节点是环分支节点，在本文图2的知识活动中，并没有知识活动环，所以强联通矩阵Q和单位矩阵I的表现形式是一样的。由图2可以得到的可达矩阵R与强联通矩阵Q，表示如下：

利用上面的方法，可以分解并得到组织完整的企业与科研学术界合作的知识流程系统的描述，而且分解与描述的结果具有唯一性。本文拟采用公式(1)来综合反映知识流程的优劣，并引入粒子群优化算法对这个知识流程形成的矩阵进行优化。

其中fi表示第i个指标与理想指标的误差的绝对值，ωi表示权值。fi越小则表示优化的结果越好，因此以fi为目标函数，就是要使其值达到最小。对矩阵最优化的目标函数为：

这是一个非线性优化问题，目标函数不易直接计算，本文拟采用粒子群优化算法来解决此问题。

(三)PSO算法

1995年，Kennedy和Eberhart博士受人工生命研究结果的启发，提出一种基于群体智能的进化计算方法，叫做粒子群优化算法(Particle Swarm Optimization，PSO 算法)［5］。PSO算法从开始提出到现在，受到了广泛的关注和研究，并成功运用于聚类、预测理论和函数优化等领域。PSO算法是一种实数域内的进化算法，在该算法中，维搜索空间上的每一个点都是优化问题的潜在解，并称之为“粒子(Particle)”，所有的粒子都有一个相应适应值和速度，目标函数决定粒子的适应值，粒子们的飞行方向和距离则决定它们的速度，粒子们总是追随当前最优的粒子，并在全局解空间中搜索最优的值。

PSO算法首先把一群随机的粒子初始化，再通过叠代计算，找到最优的值。在每一次的叠代计算中，粒子们通过跟踪两个“极值”来更新自己，第一个极值是粒子自己所找到的最优值，这个最优值叫个体极值(PBest);另外一个极值是整个粒子群目前找到的最优值，这个最优值叫做全局极值(GBest)。每一个粒子都知道当前个体的最优值，也知道整个群体中的最优值和与其对应的位置，并且能跟踪当前最优的粒子。基本的粒子群模型是在一个n维的空间里，由m个粒子，还有与进化代数t相关的粒子位置Pjt和粒子速度Vjt构成，表示为：

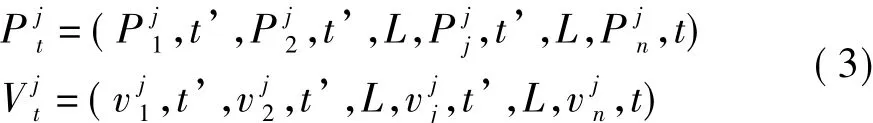
(3)式中 J=1，2，L，m 表示粒子的编号;i=1，2，L，n表示粒子位置元素的编号;t是进化代数。在t+1代时，粒子J的速度更新表达式为：

粒子的位置更新表示式为：

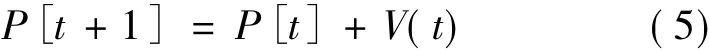
其中 C1，C2是常数，Rand()是在［0，1］区间内均匀分布的随机数，ω是一个影响PSO算法收敛性的重要参数，可以用来控制粒子的历史速度对当前速度的影响程度，本文根据Eberhart指出［6］，选取ω=0．8。

针对产学研合作技术交流中的知识流程产生的邻接矩阵的特点，在PSO算法中设计用二进制表示的12位的粒子，如表1所示。其中第1至第9位表示邻接矩阵的每一个行向量，即每一个知识流程的路径选择，第10至第12位表示邻接矩阵的行数，即为每一个知识流程的步骤。

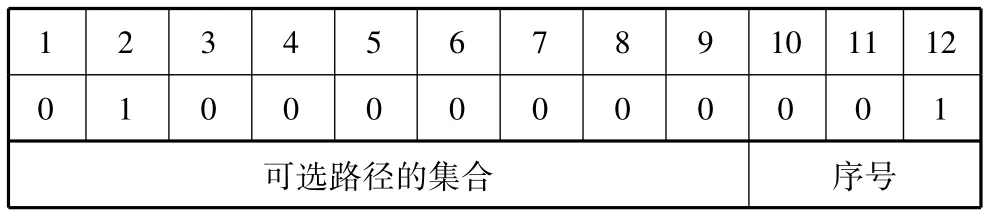
表1 粒子编码设计

每一个知识流程的路径选择算法为：

Position=Rand()

//产生一个随机值用于选择位置

While

{

If(Substr(Swarm，Mod(Position，10)，1)=1)

//判断随机选择的位置是否在可选的位置集合里

Position=Mod(Position，10) //在备选集合中随机选择一个位置

Exit

Else

Position++

//如果不在可选位置集合里，则前移找另一个，直到找到为止

}

根据表1的粒子设计以及每一个知识流程的位置选择算法，优化邻接矩阵的PSO算法框架如下：

1)粒子初始化，粒子为1维数组(Swarm［ai］)，设定粒子数目N，最大迭代次数为Tmax，在规定的范围内随机产生粒子的速度和位置;

2)根据当前的位置和速度，计算每个粒子的新位置;

3)把每个粒子代入到目标函数(1)式中，求解适应度即，最大特征值fmax。如果求解出的该适应度值好于历史最优值(PBest)，则令当前的求解值作为新的极值，在所有的历史最优值PBest中选取最好的值作为全局的最优点(GBest);

4)粒子的速度和位置按(4)式和(5)式更新;

5)判断是否达到迭代的终止条件，即一个预设好的最大迭代次数Tmax，如果t≥Tmax则迭代终止，否则t=t+1，返回第3)步重新进行新一轮的迭代。

该PSO算法用Matlab PSO工具箱实现，算法中的参数设置如下：c1=c2=2;rand()∈［0，1］的随机数;ω=0．8;粒子数目d=20;迭代次数的最大值为Kmax=100。通过迭代计算，得出 f=6．3733，权值 ω=(1，0．7428，0．2257，0．7743，0．8256，0．8632，0．7475，0．3381，0．6619)T可作为参考。知识流程分析法是系统工程中十分典型的定量分析和定性分析的综合集成方法，在各种实际复杂系统综合评价和多目标决策中得到了广泛的应用。建模与优化是产学研合作知识流程中无法回避的关键问题。本文采用混合流程图对该知识流程进行描述，并在此基础上进行深入的数学分析。通过对产学研合作创新过程中企业获取知识的活动建模，针对产学研合作交流创新中技术交流生产的邻接矩阵问题，提出以邻接矩阵与理想要求的误差最小为目标，建立求解权值准则，优化目标函数，引入PSO算法解决此问题。实例表明，对产学研合作创新使用知识流程方法来分析是有效的，计算结果对企业向学研方购买技术以及促进产学研合作创新具有一定的理论指导意义。

三、结束语

在企业和学术科研界的合作创新中，不论准备开展什么样的知识管理流程，都一定要围绕知识获取、知识应用、知识创新和知识共享这四方面来进行。高效能地创新知识和高效率地应用知识是所有产学研合作创新运作的目标。随着国家对学术科研界科技投入的增加，科研界的科技成果也在逐年增加，但是这些科技成果大部分都处在实验室状态，离真正走向大规模应用还尚需时日。将现有科研成果转化为生产力是迫切需要解决的问题。从地方政府角度来看，在当今国内地区竞争加剧的环境下，发展高科技产业、促进地区经济的发展、保持地区长久竞争力，促进产学研合作无疑已经成为地方政府重要的课题。

［1］成思危．论创新型国家的建设［J］．中国软科学，2009，(12)．

［2］陈程，刘和东．产学研合作创新的不对称信息博弈［J］．科技管理研究，2009，(9)．

［3］达庆利，何建敏．大系统理论与方法［M］．南京：东南大学出版社，1989．

［4］黄丽华，钱宇，薛华成．企业过程的定义及辨识方法［J］．系统工程学报，1997，(3)．

［5］Kennedy J，Eberhart R．Particle swarm optimization［C］．Proceedings of IEEE International Conference on Neural Network，Perth(Australia)，1995：1942-1948．

［6］Saravanann，Waagend，Eibenae．Genetic Algorithms and Particle Swarm Optimization［J］．In Porto Evolu-tionary Programming Springer，1998，VII：611—616．