基于PSO-RBF神经网络的模拟电路故障诊断研究
2011-01-24郭珂,伞冶,朱亦
郭 珂, 伞 冶, 朱 亦
(哈尔滨工业大学 黑龙江 哈尔滨 150001)
当今社会,电子设备广泛应用于人们科研、生产、生活的各个领域。电子设备中的电路系统分为模拟电路和数字电路两个部分,数字电路由于输入输出信号比较规范,电路集成度高等自身特点决定了其出现故障的可能性较小,而且即使出了故障也比较容易诊断。理论分析和长期的实际使用经验均表明,虽然电子设备中数字电路部分超过80%,但80%以上的故障均来自模拟电路[1],因此模拟电路故障诊断的研究具有重要意义。
笔者首先利用主成分分析方法对故障信息作特征提取,然后采用PSO算法优化RBF网络,最后将训练好的RBF网络模型用于模拟电路的故障。
1 基于主成分分析的模拟电路故障特征提取
主成分分析(Principal Component Analysis, PCA)实质是上把高维数据信息线性投影到低维子空间中,用维数较少且相互独立的新变量来表征原变量所提供的绝大部分信息,从而简化问题处理的难度并提高信噪比。采用主成分分析方法对原始故障数据集进行预处理,可以在不损失有用信息的情况下提取出故障本质特征向量。将提取出的特征向量送入RBF网络进行处理,由于训练数据的规模得到约简,因而可以简化神经网络的结构,提高网络训练速度进而达到提高诊断效率的目的。
假定模拟电路的每一故障模式对应有c个特征参数,每种故障模式有l个样本数目,构成一个l×c原始故障样本矩阵X。
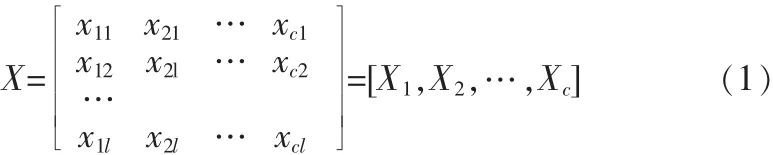
其中:Xi=[xi1,xi2,…,xil]T,i=1,2,…,c。
根据PCA方法的基本原理,给出基于PCA的故障数据压缩及特征提取算法步骤如下:
step 1:标准化
1)计算原始数据矩阵X矩阵的均值向量x¯;

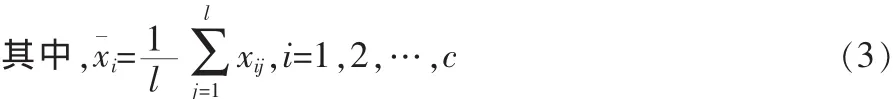
2)计算中心平移矩阵X^,即把每维数据减去相应的均值;

step 2:计算数据的协方差矩阵∑c×c
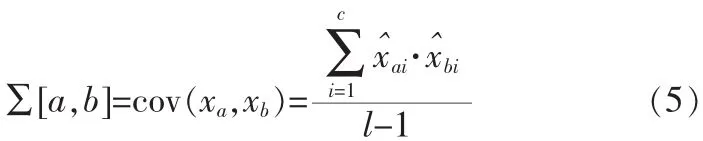
其中,a=1,2,…c;b=1,2,…,c。
step 3:对协方差矩阵∑进行特征分析,使∑P=PΛ
其中,Λ=diag[λ1,λ2,…,λc],P=[p1,p2,…,pc],它们分别是协方差矩阵的特征值和对应的特征向量。将特征值按照由大到小的顺序排列,对应的特征向量也作相应排列。
step 4:主成分个数的选取
确定主成分个数的方法有Akaike信息准则法、平均特征值法和累计方差贡献率法等,文中采用累计方差贡献率法。
1)取前 d 个 特 征 值 Λd=diag[λ1,λ2,… ,λd]和 特 征 向 量Pd=[p1,p2,…pd]作为子空间的基底,由[p1,p2,…pd]构成主元空间,由[Pd+1,Pd+2,…,Pn]构成残差空间;
2)具体如何确定d需要引入方差贡献率的定义:
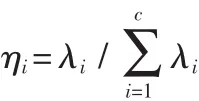
ηi称为第i个主成分pi的方差贡献率。如果只取前d(d step 5:求取故障特向量 第 i个故障特征向量为 ti=Xpi,其中,i=1,2,…,d。 径向基函数神经网络 (Radial Basis Function Neural Networks,RBF网络)是一种3层前馈网络,以函数逼近论为理论基础,模拟了人脑中局部调整、相互覆盖接收域的神经网络结构。RBF网络是一种局部逼近网络,具有结构简单、学习收敛速度快且对于非线性连续函数具有一致逼近性等优良特性,因而在函数逼近和模式分类领域中显现出比BP网络更强的发展潜力。目前,RBF网络已经广泛应用于故障诊断[2-3]、非线性函数逼近、模式识别和图像处理等领域。 图1给出了拓扑结构为n-h-m的RBF网络模型,它是一个以径向基函数φ(·)为隐层单元的三层前向网络:第一层是输入层,由信号源节点组成,仅起到传输信号的作用,其中X=[x1,x1,…,xn]∈Rn为网络输入向量;第二层是隐层,隐单元的个数由所描述的问题而定,其中W∈Rh×m为输出权矩阵;第三层是输出层,对输入模式做出响应,通常是简单的线性函数,其中 y=[y1,y1,…,yn]∈Rm为网络输出,第 k 个输出可以表 图1 RBF神经网络结构图Fig.1 Structure of RBF neural networks 常用的径向基函数有Gaussian函数、多二次函数、逆多二次函数和反射Sigmoid函数等,文中采用广泛使用的Gaussian函数作为隐层单元的基函数。RBF网络的学习过程通常可以分为两步:第一步确定隐层节点的选取,包括节点个数h、中心位置ci和宽度σi;第二步确定隐层与输出层之间的连接权矩阵W。通常情况下,当隐层节点个数以及中心位置、宽度确定后,隐层与输出层之间权矩阵W的求取就可以采用线性优化策略,因而隐层节点数量和中心的确定是RBF网络设计的核心问题。常用的学习算法有进化优选法、Kohonen中心选择法、k-means聚类方法、梯度训练方法以及正交最小二乘法等。尽管Chen等声称正交最小二乘算法能设计出最小结构的RBF网络[4],但Sherstinsky和 Picard给出了反例[5],因而目前为止还没有某种方法能够在理论上求得上述参数的最优值,只能通过大量的实验进行试凑。基于此,采用粒子群优化算法来训练RBF网络。 粒子群优化算法(Particle Swarm Optimization,PSO)是一种全局优化进化算法,它结构简单易于实现、需要调整的参数较少,具有较强的全局收敛能力和鲁棒性,能够有效解决较为复杂的优化问题。在粒子群算法中,优化问题的每个可行解都看作搜索空间中的一个点(称之为粒子),通过适应度函数值来评价每个粒子对应可行解的优劣。粒子具有位置和速度两个属性,它根据自身和同伴的飞行经验来优化调整自己的位置和速度,迭代一定次数之后就会得到搜索空间中的全局最优解。粒子群算法的数学描述如下[6]: 假定一个由M个粒子组成的群体在D维搜索空间中以一定速度飞行,其中第i个粒子的位置和速度分别表示为Xi=(xi1,xi2,…,xid)和 Vi=(vi1,vi2,…,vid)。 用 pi=(pi1,pi2,…,pn)表示粒子自身迄今为止找到的最优解,pg=(pg1,pg2, …,pgn)表示整个种群迄今为止找到的最优解。粒子在找到pi和pg之后通过如下规则来更新自己的状态: 式中,c1和c2为加速常数,它们表示粒子受社会知识和个体认知的影响程度,通常设为相同值,Clerc推导出,c1=c2=2.05,r1和 r2为介于(0,1)之间的随机数;w为惯性权重因子,用于均衡粒子的全局探索能力和局部开发能力;vtid和xtid分别为粒子i在第t次迭代中第d维的速度和位置;ptid为粒子i在第d维的个体极值位置,ptgd为群体在第d维的全局极值位置。 实现PSO算法优化RBF网络时需要解决如下3个问题: 1)参数编码策略的选取 编码方式通常分为向量编码和矩阵编码,文中采用向量编码策略。在向量编码策略中,每个粒子被编码为一个向量,图1所示的RBF网络编码后粒子位置和速度的维数为h×(n+1),RBF神经网络隐层编码策略如图2所示。 图2 RBF神经网络隐层编码策略Fig.2 Coding strategy for hidden layer of RBFNN 2)适应度函数的选取 网络优化的最终目的是找到一组最优参数使得训练样本的均方误差和最小,因此适应度函数可以选为: 3)算法终止条件的选取 算法终止条件的选取必须同时兼顾算法的学习精度和速度,通常为达到所要求的适应度阈值或者达到预先设定的最大迭代次数。PSO-RBF算法流程图如图3所示。 图3 PSO-RBF算法流程图Fig.3 Flow chart of PSO-RBF algorithm 为验证文中所提方法的有效性,采用如下两级三极管放大 图4 两级放大电路Fig.4 Two-level amplifying circuit 令C代表三极管集电极,E代表三极管发射极,令B代表三极管基极,OC代表开路故障,SC代表短路故障,建立表1所示的故障模式表。电路作为待诊断电路,电路中各元件参数值已在图4中标出。 表1 故障模式表Tab.1 Table of fault mode 通过Cadence/OrCAD/PSpice电路仿真软件对电路各种故障状态进行仿真,开路故障模型用100 MΩ电阻和开路元件串联,短路故障模型用1Ω电阻和短路元件并联。图5是电阻R1短路故障时的仿真电路图,其他故障情况类似,因而不再一一给出。 图5 电阻R1短路故障仿真电路图Fig.5 Simulation circuit of resistance R1 short circuit fault 在图4电路中共选取8个电压测试节点:V1,V2,…,V6。为了便于进行下一步的故障特征提取,将测得数据进行归一化处理,表2给出了用于训练的一组归一化处理后的数据。 为了减少RBF网络的输入向量维数,提高其训练速度,对表2中的数据进行主成分分析,主成分分析后的数据如表3所示。图6是前4个主成分的累积方差贡献率图,从图6中可以看出,前4个主成分的贡献率分别为45.98%,30.48%,13.60%和8.51%,前3个主成分的累积方差贡献率为91%,前4个主成分的贡献率已经达到了98.6%,文中选取前4个主成分作为RBF网络的输入。在网络训练过程中,隐层节点数选为6个,初始粒子数目经过多次试验后确定为20个,网络训练误差曲线如图7所示。 表2 电压测试数据Tab.2 Table of voltage measurement data 图6 累积方差贡献率图Fig.6 Cumulative variances contribution rate 对各种故障情况下的放大电路进行300次Monte-Carlo实验,将所得数据作为测试数据输入训练好的网络用于故障诊断,经过300次的测试统计,所得故障诊断正确率如表4所示。可看出,文中所提方法的诊断效果较为理想,所有故障状态的诊断正确率都能达到80%以上,其中一半以上的故障诊断正确率超过了95%,从而验证了该方法的有效性。 模拟电路广泛应用于生产、生活的各个领域,因而对其进行故障诊断研究具有重要现实意义。本文针对模拟电路传统诊断方法的不足之处,提出采用基于粒子群优化的RBF网络进行故障诊断,将主成分分析方法用于模拟电路的故障特征提取,从而约简了网络结构,提高了网络训练速度。在两级放大电路的故障诊断实例中,高达80%以上的故障诊断正确率验证了该方法的有效性和实用性。 表3 主成分分析后的测试数据Tab.3 Table of measurement data processed by PCA 图7 网络训练误差曲线Fig.7 Curve of training error for neural networks 表4 故障诊断正确率列表Tab.4 Table of diagnostic accuracy [1]Li F,Woo P Y.Fault detection for linear analog ic-the method of short-circuit admittance parameters[J].IEEE Transactions on Circuits and SystemsⅠ:Fundame, 2002, 49(1):105-108. [2]代睿.一种基于RBF神经网络的智能故障诊断方法[J].北京联合大学学报:自然科学版,2009,23(2):30-33.DAI Rui.Intelligent fault diagnosis based on RBF neural network[J].Journal of Beijing Union University:Natural Sciences,2009,23(2):30-33. [3]秦庆强,张晓安,李艾华,等.基于RBF网络的模拟电路故障诊断算法[J].计算机仿真,2010,27(5):331-335.QIN Qing-qiang,ZHANG Xiao-an,LI Ai-hua,et al.Algorithm based on RBF artificial network for analog circuit faultdiagnosis[J].Computer Simulation,2010,27(5):331-335. [4]Chen S,Cowan N C,Grant P M.Orthogonal least squares learning algorithm for radial basis function networks[J].IEEE Transactions on Neural Networks, 1991, 2(2):302-309. [5]Sherstinsky A,Picard R W.On the efficiency of the orthogonal least squares training method for radial basis function networks[J].IEEE Transactions on Neural Networks,1996,7(1):195-200. [6]Shi Y,Eberhart R C.A modified particle swarm optimizer[C]//Proceedings of the IEEE conference on Evolutionary,1998:69-73.2 基于PSO优化的RBF神经网络
2.1 RBF神经网络
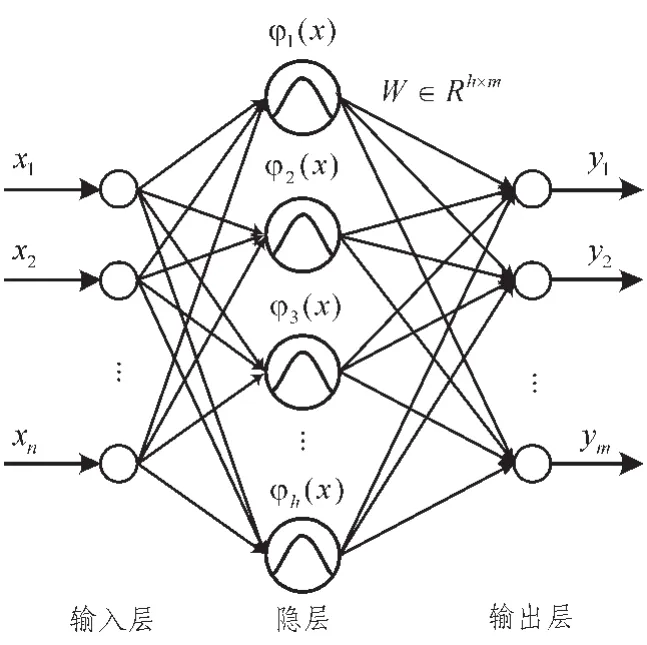
2.2 粒子群优化算法
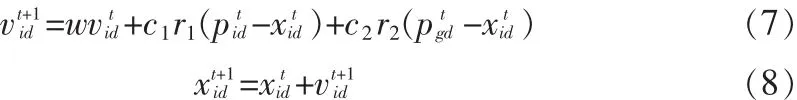
2.3 PSO-RBF算法实现
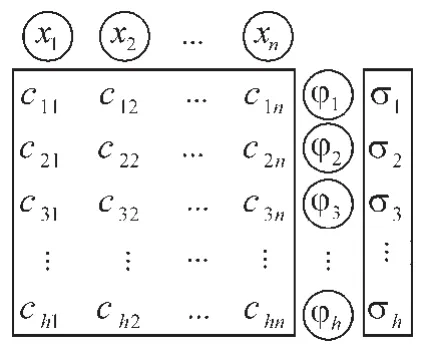
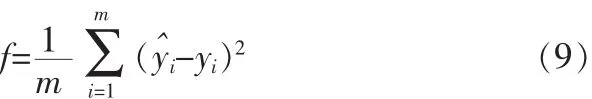
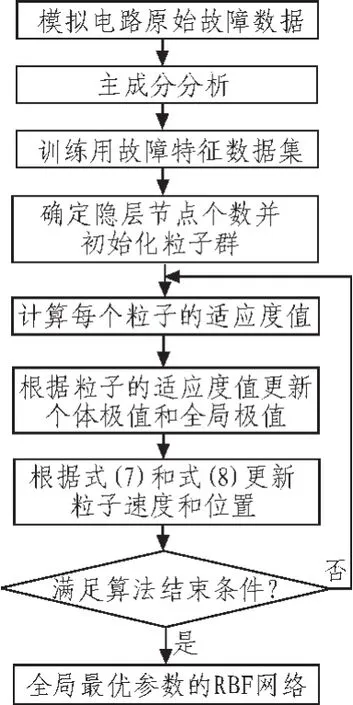
3 诊断实例
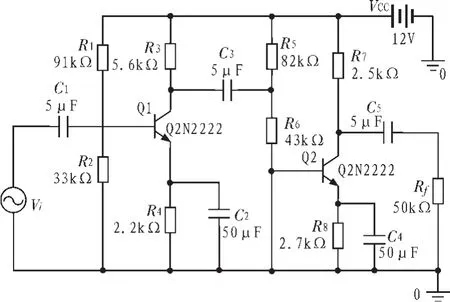

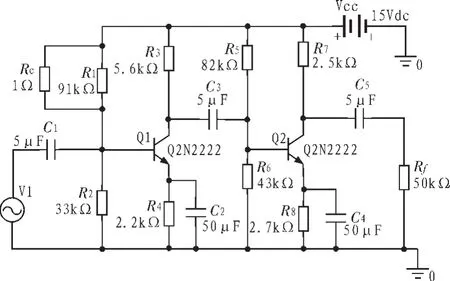
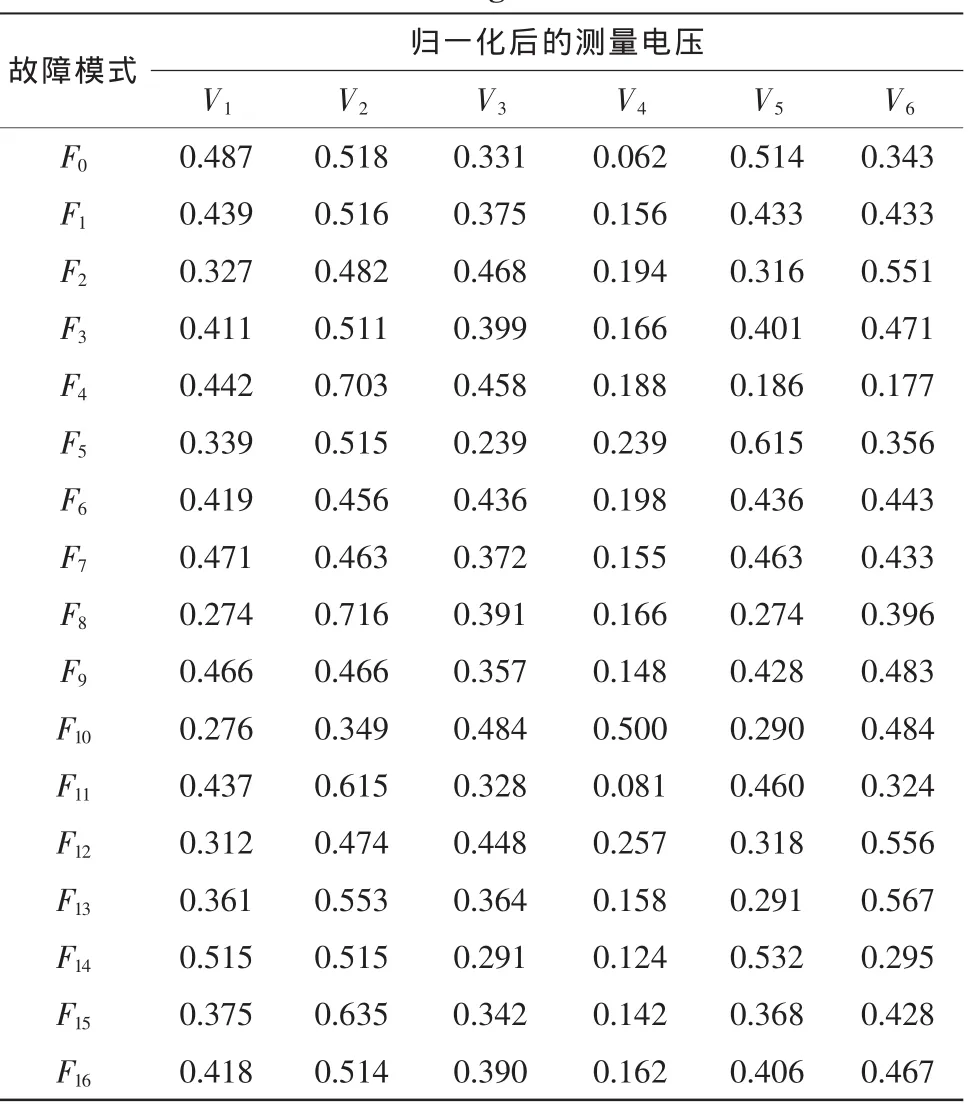
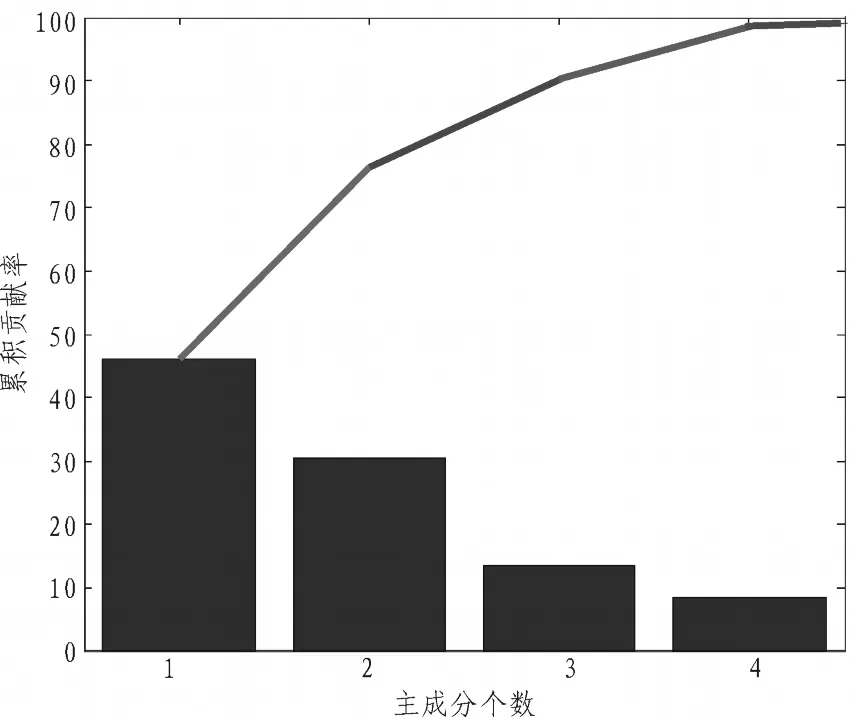
4 结 论