带电粒子在复合场中运动的三个问题的再探讨

姜付锦

(武汉市黄陂区第一中学 湖北 武汉 430030)

《物理通报》2010年第3期胡均宇《关于带电粒子在复合场中运动的题目误解分析》中对三个题目作出了判断：题目由于条件不足，不能求出小球在最低点运动的速度和下落的高度.笔者认为这三个题目在高中阶段是能做出来的.以下就是笔者的分析过程.

【题目1】如图1，一电荷量为+q的小球固定在与水平面平行的足够大的匀场磁场中.若匀强磁场的磁感应强度大小为B，小球的质量为m，自由释放小球.试分析小球的运动情况并求出带电小球下落的高度.

解法一：利用动量定理与动能定理求解

图1

由题意可知，带电小球在运动过程中受到重力和洛伦兹力作用，其中只有重力做功，所以小球的机械能守恒.设小球在最低点的速度为vm，则其速度一定为水平方向.设小球下降的最大高度为h，则有

洛伦兹力虽不做功，但产生冲量，把小球在某一时刻的速度分解为水平和竖直两方向，水平分速度产生的洛伦兹力竖直向上，竖直分速度产生的洛伦兹力水平向右，则由动量定理可知，小球在水平方向上的动量改变为

mvm=∑Bqvy·t=

Bq∑vy·t=Bqh

由上两式联立可求得

解法二：利用运动的合成与分解求解

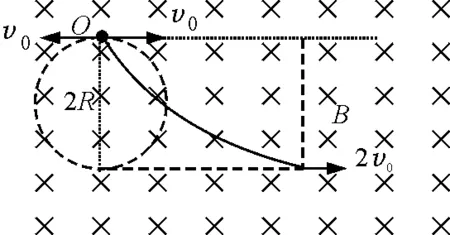
图2

如图2，设开始时小球向左和向右各一个初速度，大小均为v0，且

Bqv0=mg

则带电小球的运动可分解为两个运动:在水平方向上做速度大小为v0的匀速直线运动，和在竖直方向上做速度大小为v0的匀速圆周运动.向心力

则

其中轨迹的最大高度为

最大速度为

解法三：根据韦达定理求解

如图1,设带电小球在最低点的速度为vm，下落的高度为h，最低点对应的曲率半径为ρ，则由动能定理得

由最低点的向心力公式得

将向心力公式整理后得

mvm2-ρBqvm+mgρ=0

方程中速度只有唯一解，所以

Δ=(ρBq)2-4m2gρ=0

求得

【题目2】如图3，两极板间存在磁感应强度为B的匀强磁场，静止在负极板附近的带负电微粒，质量为m1、电荷量为-q，在MN间突然加上匀强电场E时开始运动，水平击中速度为零的中性粒子m2后，粘合在一起恰好沿一段圆弧运动到N极板上.求m1击中m2时的高度，m1击中m2前瞬时速度，m2的质量及m1和m2粘合体做圆弧运动的半径.

图3

解析:由题目1中的解答结果可知

设粒子m1在复合场中的等效重力加速度

代替上式中的g即可，所以

根据题意可知m1、m2在相碰时动量守恒.设碰后的速度为v，则有

m1vm=(m1+m2)v

碰后两粒子恰好做匀速圆周运动，所以

Eq=(m1+m2)g

可求得

碰后系统做匀速圆周运动，所以向心力

求得

将v,m2的关系式代入后,得

【题目3】倾角为θ足够长光滑斜面处于磁感应强度为B的匀强磁场中，磁场方向垂直纸面向里，如图4所示.若一电荷量为-q的小物体从顶端由静止开始下滑，已知小物体的质量为m.求：

(1)小物体离开斜面时的速度；

(2)小物体沿斜面下滑的距离；

(3)小物体离开斜面后的最终速度大小.

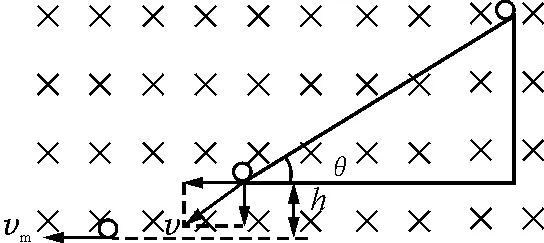
图4

解析:由垂直斜面方向上的平衡条件和机械能守恒定律可求得

qvB=mgcosθ

解得

由

解得

设粒子离开斜面后在最低点时的速度为vm，下落的高度为h，则由水平方向上的动量定理有

∑Bqvy·t=m(vm-vcosθ)=Bqh

由粒子的机械能守恒得

联立以上两式可求得

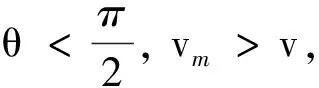
带电粒子离开斜面后没有最终速度，只有最大速度且此时带电粒子受的洛伦兹力大于重力，所以它会再向上减速运动.