动生电动势与感生电动势的统一
2011-01-24林辉庆
林辉庆
(余杭高级中学 浙江 杭州 311100)
对感应电动势根据非静电力来源的不同,分为动生电动势和感生电动势两类.导体在磁场中运动,其中的自由电荷受到洛伦兹力,从而推动自由电荷定向移动,这样产生的感应电动势叫动生电动势;由于磁场变化产生涡旋电场,导体中的自由电荷受到涡旋电场的作用力而定向移动,这样产生的感应电动势叫感生电动势.这两种感应电动势的大小,都满足法拉第电磁感应定律
高中生经常提出这样的问题:既然动生电动势和感生电动势的非静电力来源不同,它们怎么会满足相同的定律?它们能否在更深的层次上相统一?一些大学的电磁学教材没有涉及这个问题,有些教材虽然涉及到了这个问题,但没有使它们真正相统一.本文对此问题做较为深入的探讨.
1 动生电动势与感生电动势的相对性
动生电动势与感生电动势的区分并非是绝对的,而与选取的参考系有关.对于具体的电磁感应现象,在一个参考系中观察是动生电动势,在另一个参考系中观察就可能是感生电动势.如图1所示,柱形磁棒与导体圆环相对运动,导体圆环中出现感应电动势.如果以磁棒为参考系,那么空间各点的磁场不变,导体环切割磁感线产生感应电动势,如图1(a),这时的电动势就是动生电动势.如果以圆环为参考系,那么空间各点的磁场都在变化,变化的磁场产生涡旋电场,涡旋电场使导体圆环中产生感应电动势,如图1(b),这时的电动势是感生电动势.

图1
动生电动势与感生电动势的相对性表明它们是相互联系、相互转化的.两者的联系和转化,一定源于磁场与电场的联系和转化.实际上,按照麦克斯韦的电磁理论,电场和磁场是相互联系、相互转化的统一体,称为电磁场.从相对论可以更好地理解这一点.在相对论中,电场和磁场只是统一的电磁场的两种不同表现,一个电磁场,在某个参考系中观察,它可能表现为电场,在另一个参考系中观察,它可能就表现为磁场,在一般的情况下,观察到的是既有电场又有磁场.电磁场在不同参考系之间作为一个整体来变换.动生电动势与感生电动势的非静电力——洛伦兹力和涡旋电场力,是电磁场对导体中自由电荷统一的电磁作用力的两种成分.这两种成分是相互联系、相互转化的,这决定了这两种电动势必然是统一的.
下面用两个参考系之间的相对论变换,探讨动生电动势与感生电动势的定量统一.为此,先研究电源电动势在不同参考系之间的相对论变换.
2 电源电动势的相对论变换
电源是通过非静电力做功把其他形式的能转化为电能的装置.电能的实质是电源正、负极积聚的正、负电荷相互作用具有的电势能.电源的电动势定义为非静电力把正电荷在电源内从负极移送到正极所做的功W与所移送电荷量q的比值.非静电力做了多少功,就有多少其他形式的能转化为电势能.所以,电动势E也等于非静电力移送电荷增加的电势能ΔE,与被移送电荷q的比值,即
那么,在做相对运动的不同参考系中观测,同一电源的电动势是否相同?电动势与非静电力做功产生的电势能的变化相联系.由相对论,能量E总对应一定的质量m,即
E=mc2
同一对象,在不同参考系中观测,质量不同.设物体的静止质量为m0,则在与物体的相对运动速度为v的参考系中观测,质量为
c是真空中的光速.在相对论中,一个过程的能量变化,在不同参考系中观测,有不同的数值.所以,同一个电源,在不同参考系中观测,电动势也不相同.
设非静电力把一定量的电荷从的电源的负极运送到正极,在相对电源静止的参考系K′ 和相对电源以速度v运动的参考系K中观测,电势能分别增加了ΔE′ 和ΔE;与它们对应的质量变化分别为Δm′ 和Δm.由质量变换关系有
由质能关系得到
(1)
电荷量是一个洛伦兹不变量,在不同参考系中观测,同一个带电粒子的电荷量q相同.在(1)式两边同除以q,即得到
(2)
这就是电源电动势在不同参考系之间的变换公式,其中 E ′是在相对于电源静止的参考系中的电动势,E是相对于电源以速度v运动的参考系中的电动势.可见电源在运动状态的电动势大于静止状态的电动势.
3 动生电动势与感生电动势在相对论中的统一
为了推导方便,下面只研究导体棒在匀强磁场中切割磁感线这种最简单的情况,而得到的结果具有普遍性.
在图2所示的K参考系中,PQ、MN之间有沿z轴负方向的匀强磁场(图中z轴未画),磁感应强度为B,长为l的导体棒CD沿y轴方向,以速度v沿x轴方向运动.
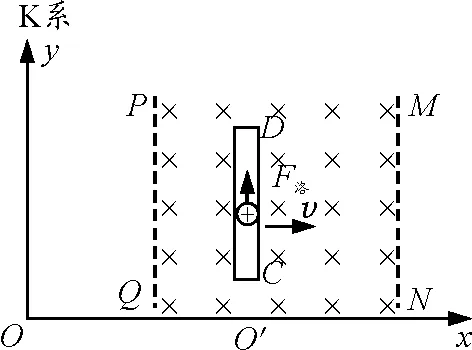
图2
设导体棒中的自由电荷带正电,它随着棒运动而受到y轴方向的洛伦兹力
F洛=qvB
自由电荷从C端运动到D端,由于洛伦兹力做功而增加的电势能为
ΔE=qvBl
电动势
(3)
如图3所示,在与导体棒一起运动的K′参考系中观测,空间既有电场又有磁场.根据电磁场的相对论变换,可以由K参考系中的磁场,求出K′ 参考系中电磁场的各个分量.
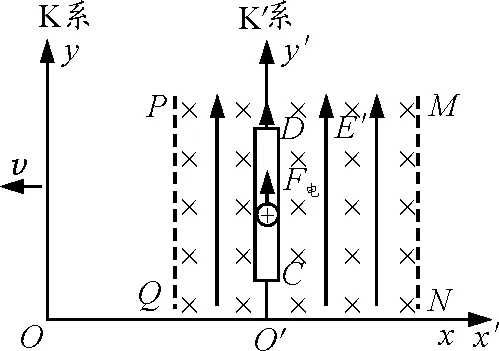
图3
从K参考系到K′ 参考系,电磁场的变换公式为[1]
(4)
变换式中
在K参考系中,电磁场中的各个分量为Ex=
Ey=Ez=0,Bx=By=0,Bz= -B.由变换公式(4)得到在K' 参考系中,电磁场中的各个分量为Ex′=Ez′=0,Ey′=γvB,Bx′=By′=0,Bz′= -γB.
在K′参考系中,导体棒中的自由电荷受到感应电场力(非静电力)从C端运动到D端,增加的电势能ΔE′=qEy′l=qγvBl.电动势为
(5)
比较(3)、(5)两式得到
(6)
在这里,与导体棒相对静止的参考系K′ 中观测到的电动势E ′,比相对导体棒运动的参考系K中观测到的电动势E 大,与电源电动势的变换公式(2)相矛盾.
问题出在哪里?原来,在推导K参考系中的电动势公式(3)时,并没有考虑相对论效应.自由电荷在沿y轴方向的洛伦兹力作用下从C端移动到D端,电势能增加,导体棒的质量也增大.要使导体棒以速度v沿x轴方向匀速运动,需要再增加一个x方向的外力Fx,才能使导体棒水平方向的动量增加.
即Fxdt=vdm
(7)
自由电荷从导体棒的C端运动到D端的过程,水平外力Fx做的功
利用(7)式得到
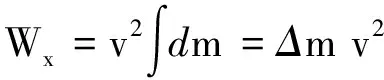
(8)
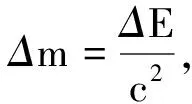
(9)
电荷q从C端运动到D端,对导体棒做功的非静电力有y轴方向的洛伦兹力和x方向的外力Fx,由功能关系有
qvBl+Wx=ΔE
利用(9)式即可得到
电动势为
(10)
比较(5)式和(10)式,即可得到
与电源电动势的相对论变换公式(2)符合.
至此,我们在相对论的理论框架内,达到了动生电动势与感生电动势的定量统一,并且推导出了相对论中动生电动势的公式
由此知道,通常使用的动生电动势公式E =Blv,是相对论中动生电动势公式在导体棒的速度v远小于光速c情况下的近似.
参考文献
1 赵凯华,陈熙谋.新概念物理教程·电磁学(第二版).北京:高等教育出版社,2006.199
