分区均匀介质静电场的求解
2011-01-24秦敢
秦敢
(中国科学技术大学物理学院 安徽 合肥 230026)
1 分区均匀介质静电场求解方法的回顾
分区均匀介质静电场的求解是电磁学课程中比较有难度和有特色的内容.有两种情形的分区均匀介质静电场问题可以解析求解:一种是介质-介质界面与撤去电介质时的电场线平行;另一种是介质-介质界面与撤去电介质时的电场线垂直.它是唯一性定理应用的一个生动的实例,并且涉及到静电学诸多原理的综合应用.考虑到很多教材不涉及此内容,这里先对此类问题求解方法作简要回顾.
1.1 介质-介质界面与电场线平行
设空间存在若干导体和均匀各向同性电介质,介质-介质界面与撤去电介质时的电场线平行,或形象地表述为,电介质按电场线管充满,如图1(a).

图1 介质-介质界面与电场线平行
常见的两种情况是:平板电容器中填充两种电介质,介质-介质的界面和撤去电介质时的电场均为竖直方向,如图1(b);球形电容器中填充两种电介质,介质-介质的界面和撤去电介质时的电场均为径向,如图1 (c).可以证明,加上电介质前后电场分布形式不变,即E=αE0,其中E0为无介质时自由电荷的电场.理由如下.
(1) 若上解成立,则P在介质-介质界面无法向分量,根据σe′=-(P2-P1)·n,界面σe′=0,所以极化电荷只可能存在于导体-介质界面.
(2) 为保证导体内恒无电场,有介质时导体-介质界面的总电荷 (自由电荷+极化电荷) 必须与无介质时导体表面的自由电荷有相同形式的分布,即σe=ασe0.这一点是由导体中自由电荷可以随意流动来实现.
(3)由电场与电荷的线性关系得E=αE0, 正如猜想.
本解能保证导体边界为等势面.由唯一性定理,该解是唯一正确解.
由此得到此问题的求解步骤为,设无介质时的各区域电场E0i已知,由高斯定理
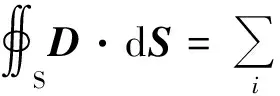

求出α,进而有
Ei=αE0i
特别是对于一维对称问题,E0有统一的表达式,可直接计算E,不必引入α,因为上式可以简化为

1.2 介质-介质界面与电场线垂直
设空间存在若干导体和均匀各向同性电介质,其中介质界面与撤去电介质时的电场线垂直,或形象表述为,在等势面之间填充各种电介质,如图2(a).常见的两种情况是:平板电容器中填充两种电介质,介质-介质的界面平行于极板,如图2(b);球形电容器中填充两种电介质,介质-介质的界面为球面,如图2(c).

图2 介质-介质界面与电场线垂直
此时的解为
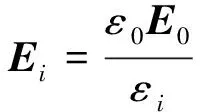
其中E0为无介质时自由电荷的电场.理由如下:
(1)ε0E0满足D的高斯定理
SD·dS=Q0
这是因为
即
Sε0E0·dS=Q0

参照图2(a),则因为
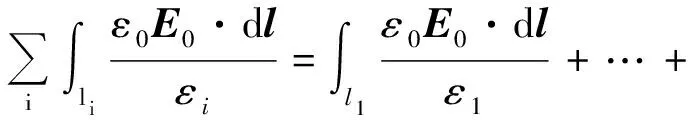

尽管上述两类解析方法原则上能求解更广泛的问题,但在实际的例题和习题中,几乎全部都是处理平板电容器和球形电容器这样的简单情况.也许有个很自然而且强大的理由:其他形状边界的例子依然有解析解,只是因为太复杂琐碎而不予讨论.毕竟平庸的复杂对于原理的领悟是不必要的.
一切看上去风平浪静.但在长期的教学过程中,偶然性地发现了“异常”情况.
2 两种分区情形同时存在时的求解
如图3,平板电容器内填充三类电介质,能否解析求解各介质的电场?

图3 两种分区情形同时存在
一种常见的解法是:将各介质当作独立的电容器,用电容器的串、并联来求解,即介质2的电容器与介质3的电容器串联后再与介质1的电容器并联.这种方法本质上就是前述两种分区介质求解方法的综合运用——介质2与介质3构成的子体系对应界面与电场线垂直的情形,而该子体系与介质1构成的体系则对应界面与电场线平行的情形.
其实,通过对边值关系的简单分析就能看出来错误所在.若单一分区均匀介质静电场解法对这种混合问题仍然有效,则平板电容器内各个区域的电场强度均沿竖直方向.由电场强度的边值关系,介质1-2界面处有E1=E2,介质1-3界面处有E1=E3,于是E2=E3.可是在2-3界面处的边值关系本来是D2=D3,两者矛盾!可见,单一分区均匀介质静电场的求解方法对两种分区共存的情况是无效的.
该问题无解析解的实质原因何在?容易想到的是,与两种单一的分区情形不同,两种分区共存的情形过于复杂,电场线 (或电位移线) 不再能保持无介质时的分布形式.
也可以这样间接地理解:如果该例有解析解,则电介质区域作进一步分割后仍会有解析解 (无非是更复杂的电容器串并联而已),以至于任何电介质分布下都可解析求解,这当然是不可能的.
这里讨论的是严格解,如果忽略竖直边界的边缘效应,则常规的串并联方法是可行的.其实,对此例的“吹毛求疵”,更多的目的是作为引子,引发对分区均匀介质静电场问题的进一步探索.
3 介质-介质界面与电场线平行时解析解存在的条件
单一分区与两种分区共存真的就是简单与复杂的界限吗?或者说,单一分区情形一定可以按前述方法求解吗?至少对介质界面平行于电场线的情形就存在疑问:关系式σe=ασe0在任何情况下都有效吗?
如图4,导体1和2分别带电Q1和Q2,电介质填充在导体1发出的、趋向无穷远处的电场线管内.此时σe=ασe0和E=αE0一定能成立吗?

图4 介质填充在一个开放的电场线管
假设导体1表面自由电荷的流动性使得加入介质后总电荷面密度的分布与无介质时自由电荷面密度的分布成比例.由于极化电荷与自由电荷异号,所以比例系数α<1.但α是全局常数,这就要求导体2上的总电荷面密度有同样的“衰减”,于是总电荷量必须作同样程度的减少.但导体2上只有自由电荷,加入介质前后的电荷总量应该是不变的.可见,对这样的单纯边界问题,文献[1]中方法失效.
再看稍微复杂一些的情况:电介质填充在导体1和2之间的一个电场线管,能否求解?

要想E=αE0在全空间成立,必须有
则
Q1=-Q2
除此以外,有、无介质时的电场不会成比例分布.

图5 介质填充在两导体之间的电场线管
问题出现在什么地方?文献[1]中方法有效的关键前提是,体系的确能够保证有介质时的总电荷与无介质时的自由电荷有相同分布形式,即
σe=ασe0
但这里的两个例子告诉我们,导体中自由电荷的任意流动性不足以保证在任何情况下总能做到这一点.其实这里的任意流动性并非无条件的任意,必须局限在同一导体.
由于习题中的导体通常是电容器的两个极板,带电荷为±Q,符合例2的特例,或者干脆是单一导体,所以期望的电荷分布总能做到.
需要指出的是,在求解介质-介质界面与磁感应线垂直时的静磁场问题时,文献[1]中方法有同样的限制条件.
另外,经初步分析,介质-介质界面与电场线垂直时,解析解的存在是无条件的.原因是,此问题的解法原理中没有类似E=αE0的苛刻要求.
4 结语
本文对分区均匀介质静电场求解问题中一些情形作了具体的探讨,希望有助于增加教与学的严谨性和趣味性.在探索所涉及问题的过程中,对一些电磁规律成立条件作了重新的审视,对电磁学基本原理进行了综合思考,对于简单与复杂、载流子的任意流动性有了进一步体会.
参考文献
1 胡友秋,程福臻,叶邦角.电磁学与电动力学(上册).北京:科学出版社,2008
