均匀球体转动惯量的多种求法

车晓芳

(兰州商学院 信息工程学院 甘肃 兰州 730020)

1 引言

在物理学和工程力学中，转动惯量的计算是个难点.该部分内容是学生在中学学习阶段从未接触过的，很多同学认为不好掌握.这就需要我们开拓学生的思路，培养学生分析、解决问题的能力，使学生学会主动获取知识，提高学习兴趣.为此，我们以均匀球体转动惯量的计算为例，具体说明如何扩展思路，培养学生学习的主动性.

2 转动惯量的计算

【例】求半径为R,质量为M的均匀球体绕直径的转动惯量.

解法一:由转动惯量的定义式出发，通过取质量微元的方法进行求解

取球体所绕的直径为z轴，如图1建立空间直角坐标系，该坐标系中在点(x,y,z)处任取一体积微元，该微元可近似看成一小立方体，且可视为质点，则该体积元的体积

dV=dxdydz

其质量

dm=ρdxdydz

ρ为球的质量体密.设该体积元到z轴的距离为r，则该体积元绕z轴的转动惯量为

dJ=r2dm=r2ρdxdydz

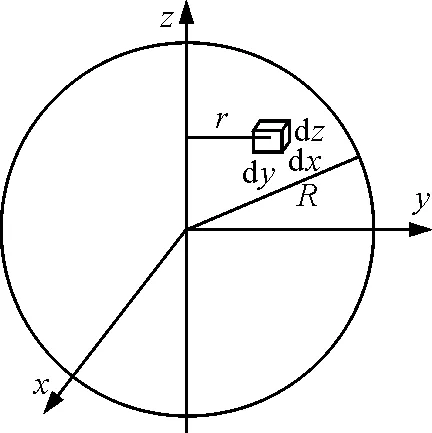
图1

其中r2=x2+y2，所以整个球体的转动惯量为

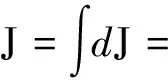
解法二:用微分法由已知球壳的转动惯量，求球体的转动惯量

可以将球体看成是由很多个半径不同的薄球壳叠加成的，所以可以取一个半径为r，厚度为dr的薄球壳，如图2所示，则该球壳的质量为

dm=ρdV=ρ4πr2dr

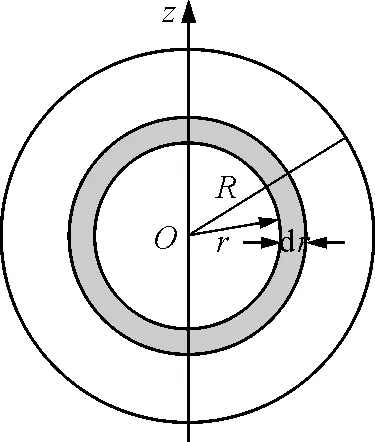
图2

绕z轴的转动惯量为

则整个球体的转动惯量为

解法三：用微分法由已知圆盘的转动惯量，求球体的转动惯量

沿垂直于z轴的方向切割球体，得到很多个薄圆台，将每个薄圆台都近似看成一薄圆盘，任取一半径为r、厚度为dr的薄圆台，如图3所示，则该薄圆台的质量为

dm=ρπr2dz

图3

它绕z轴的转动惯量为

则整个球体绕z轴的转动惯量为

解法四：用平行轴定理结合解法三，求球体的转动惯量

若沿与z轴平行的方向切割球体，也会得到很多个薄圆台，仍将薄圆台近似看成薄圆盘，取半径为r，厚度为dy的薄圆台，则该圆台绕自己直径的转动惯量为

应用平行轴定理可得它绕z轴的转动惯量为

dJ′=dJ+y2dm

则整个球体的转动惯量为

3 小结

通过上述计算过程的分析，解决了学生在转动惯量计算方面的困难，同时也提高了学生解决问题的能力，开拓了思路，有利于培养学生的学习兴趣，使学生的智力得到充分发挥.

参考文献

1 程守洙，江之永.普通物理学 .北京：高等教育出版社,2006

2 张三慧. 大学基础物理.北京：清华大学出版社,2003

3 王少杰，顾牡.大学物理学.上海：同济大学出版社，2006

4 祝之光.物理学.北京：高等教育出版社，2009

5 李自华，高等数学知识在大学物理中的应用.思茅师范高等专科学校学报,2008，6