基于RCM的冶金单体设备预防性维修模型

但斌斌，邬俊惠，容芷君

（武汉科技大学冶金装备及其控制教育部重点实验室，湖北武汉，430081）

根据实施维修活动的时间差异，可将设备维修分为两种基本类别：修复性维修（也叫事后维修）和预防性维修（也叫事前维修）。修复性维修是在设备发生意外故障后采取的维修活动；预防性维修是在设备处于运行操作过程中进行的维修活动，通过对设备进行检查、探测，及时发现和处理设备劣化倾向，将故障消除在萌芽状态，从而预防恶性故障发生，维持设备的正常运行。

冶金企业中，一些大型单体设备结构复杂，成本昂贵，对生产影响重大，如果遇故障而停机，将导致生产停顿，给企业带来巨大损失，所以需要对这些设备进行预防性维修。但预防性维修可能存在“过维修”或“欠维修”的问题。因此，为了控制设备维修成本，同时达到最佳维修效果，必须合理确定设备的预防性维修次数及周期。

以可靠性为中心的维修（reliability－centered maintenance，RCM）[1]是目前国际上通用的用以确定设备预防性维修需求、优化维修制度的一种系统工程方法。RCM结合维修过程中可靠性和经济性等多个约束条件来制定维修方案，在一定程度上提高了设备利用率，节省了维修成本。刘涛等[2]对RCM技术及其定量分析方法进行研究，建立了基于RCM的各种定量化维修模型，确立了设备的维修周期。本文以冶金企业热轧厂中的重要单体设备——开卷机为对象，运用RCM维修理念，结合定量化研究方法，建立基于可靠性和经济性约束的不完全预防性维修模型，并运用此模型对开卷机的维修次数和维修间隔进行计算。

1 模型假设条件

1.1 设备役龄

将开卷机的生命期分成若干个预防性维修周期，每个预防性维修周期分成τi和ti两部分，其中，τi为第i个周期中的开卷机工作时间，ti为第i个周期中预防性维修所花费的时间。在预防性维修期间有可能会发生意外故障，其检修时间相对预防性维修周期来说比较短，可以忽略不计[3－4]。

开卷机每经历一次预防性维修后，设备的状态或年龄都会发生变化，即相对于维修之前的状态变“年轻”，因此引入役龄回退因子对设备役龄进行修正，修正后的设备役龄为：

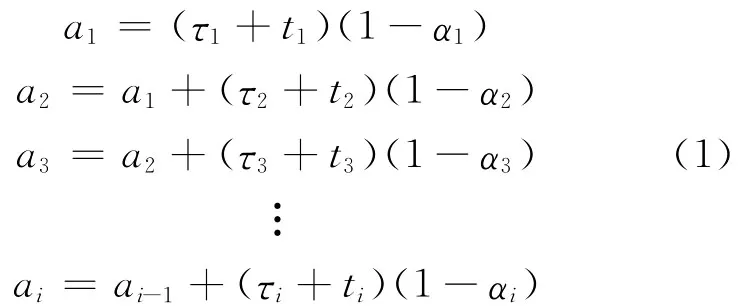
式中：αi为第i个预防性维修周期的役龄回退因子；ai为经过第i次维修后的设备役龄。

役龄回退因子是不断变化的，受设备部件的年龄、维修间隔、每次预防性维修成本等因素的影响，其中预防性维修成本是影响役龄回退因子的主要因素，可用下式表示：

式中：Cpi为第i次预防性维修的费用；Cpr为设备购置费用；a，b为调整参数。

1.2 设备故障率

预防性维修期间的故障检修属于小修，时间一般较短，因此假设小修不影响设备的故障率。预防性维修可看作是不完全维修，预防性维修后，开卷机的实际年龄采用役龄回退因子计算。设开卷机故障间隔时间的分布函数为F（t），概率密度函数为f（t），可靠度函数为R（t），有R（t）＝1－F（t），则故障率函数为[5－6]：

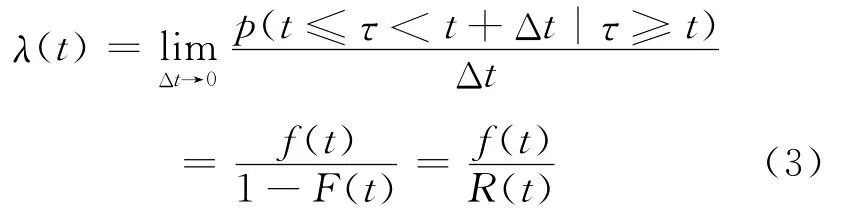
设备的可靠度函数为：

由式（3）和式（4）可得：

则设备在第i个预防性维修周期内的可靠度函数为

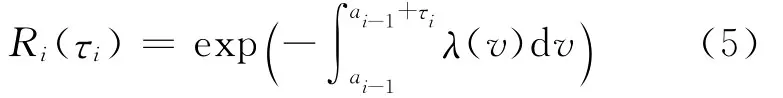
设备的故障间隔时间一般服从指数分布、正态分布、伽马分布、对数正态分布、威布尔分布和极值分布等[7]，根据对开卷机故障间隔时间的分析，本文采用威布尔分布。二参数的威布尔分布故障率函数为：

式中：η为特征寿命；m为形状参数。根据采集的设备故障间隔时间样本，利用极大似然估计法求出威布尔分布的两个参数，从而得到开卷机的故障率函数[8－9]。

2 预防性维修模型

预防性维修的总成本包括3个部分[10]：（1）预防性维修期间的故障小修成本；（2）预防性维修的成本；（3）故障检修时的生产损失。

假设在第i个预防性维修期周期内发生Qi次意外故障，则有：

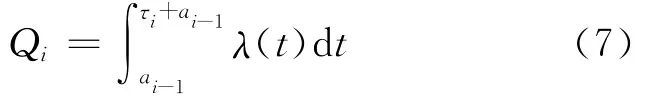
将式（6）代入式（7），计算得到：

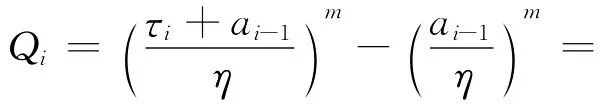
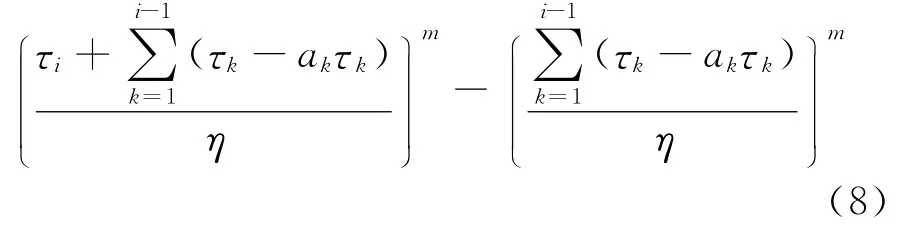
在式（8）中计算ai－1时，由于ti－1项相对于τi－1项较小，因此为了简化计算，忽略了ti－1项。

设每次小修的平均成本为Cf，则在第i个预防性维修期周期内的故障小修成本为CfQi。

开卷机的预防性维修费用与开卷机的役龄呈正相关关系，而开卷机的役龄可以用开卷机的预防性维修次数来表示，因此有Cpi＝Cu＋iCc，其中，Cu为维修中的固定成本，Cc为维修中的可变成本。

开卷机整个生命周期中的生产损失包括事后故障检修和预防性维修占用生产时间导致的生产损失。设每次意外故障所花费的平均维修时间为df，则在第i个预防性维修周期中故障检修所花费的时间为dfQi。设第i次预防性维修所花费的时间为ti，单位维修时间的生产损失费用为S，则第i个预防性维修周期中总的生产损失费用为S（ti＋dfQi）。

综上所述，开卷机预防性维修的总成本为：

式中：n为开卷机整个生命周期中的预防性维修次数。

本文基于可靠性和经济性约束建立开卷机的不完全预防性维修模型，以开卷机预防性维修总成本最小化为目标，同时应满足可靠度函数约束关系以及各种变量取值约束，即：

式中：T为设备寿命；R为设备可靠度。

3 算例

以某冶金企业热轧厂的开卷机为对象，对其预防性维修策略进行研究。通过对该设备历史维修数据的分析，利用最大似然估计法计算出开卷机故障间隔时间威布尔分布函数的两个参数分别为：m＝1.5，η＝1 500，威布尔分布函数F（t）可靠度函数R（t）＝故障率函数λ（t）＝（1.5／1 500）（t／1 500）0.5。设备购置费用Cpr＝100万元，每次预防性维修固定成本Cu＝3.5万元，可变成本Cc＝1 000元，每次意外故障小修平均成本Cf＝5 000元，每次预防性维修花费的时间ti＝24 h，每次意外故障小修花费的时间df＝2 h，占用单位生产时间造成的损失S＝1 500元，役龄回退因子的调整参数a＝12、b＝0.021，设备寿命为10 000 h，设备可靠度不得低于0.5。将上述参数带入预防性维修模型中，通过Matlab计算求解，得到该设备在运行10 000 h内的维修次数和成本如表1所示。

表1 维修次数与总成本Table 1 Maintenance times and total cost

从表1中可以看出，维修次数为11时，维修总成本最少；维修次数过多会造成“过维修”，维修成本增加；维修次数过少，形成“欠维修”，设备的可靠性太低，故障率太高，不满足可靠性约束。维修次数为11时，每个维修周期对应的时长如表2所示。

表2 每个维修周期对应的时长Table 2 Time span of each maintenance cycle

由表2可见，随着维修次数的增加，每个维修周期对应的时长逐渐变短，这与实际情况是相符的，因为随着设备役龄的增加，设备发生故障的概率也逐渐增大。

4 结语

本文应用RCM维修理念，基于可靠性和经济性两个约束条件建立了冶金单体设备的不完全预防性维修模型，利用役龄回退因子对设备役龄进行修正，较真实地反映了设备状态。该模型可以与计算机维修管理信息系统相结合，为实际维修管理提供决策信息支持。

[1] 贾希胜.以可靠性为中心的维修决策模型[M].北京：国防工业出版社，2007：56.

[2] 刘涛，蔡增杰.RCM技术研究及定量分析方法[J].科技信息，2009（36）：421－423.

[3] Malika V，Jardine A K S.Optimal replacement policy for a general model with imperfect repair[J].Journal of the Operational Research Society，1992，43（2）：111－120.

[4] Seong－Jong Joo.Scheduling preventive maintenance for modulardesigned components：a dynamic approach[J].European Journal of Operational Research，2009，192（2）：512－520.

[5] Lust T，Roux O，Riane F.Exact and heuristic methods for the selective maintenance problem[J].European Journal of Operational Research，2009，192（3）：1 166－1 177.

[6] 周正伐.可靠性工程基础[M].北京：中国宇航出版社，2009：142.

[7] 赵宇，杨军.可靠性数据分析教程[M].北京：北京航空航天大学出版社，2009：161.

[8] 曹晋华.可靠性数学引论[M].北京：高等教育出版社，2006：124.

[9] 何金定，贺星棋.考虑可修多状态的输电线路可靠性评估模型[J].电力系统保护与控制，2010，38（4）：11－14，53.

[10] 王灵芝，徐宇工，张家栋.基于设备有效度和可靠度的预防修经济优化模型[J].机械工程学报，2010，46（4）：163－168.