二维无旋超音速扩散对称流动控制方程及其特征线方程和相容性方程
2011-01-23彭宝林郭良斌
彭宝林,郭良斌
(武汉科技大学机械自动化学院,湖北武汉,430081)
高供气压力下的静压平行圆盘止推气体轴承的气膜入口流速为音速,随着通气截面半径及截面面积的增大,气流的马赫数不断增大,在等熵流中,随着气流马赫数的增大,静压降低,气体止推轴承的承载效率降低[1]。研究表明,通过改变和重新设计流道结构,使气流在气膜入口处的流速降至亚音速,或降低气膜内超音速流的马赫数,可以提高圆盘止推气体轴承的承载力。
本文采用绝热理想气体和在气膜入口处有微小平行段的变气膜厚度模型,根据无彻力定常无黏流旋度保持不变的原理,将圆盘止推气体轴承内的流场简化为在半径和气膜厚度方向上为变量的二维无旋场,推导出气膜间隙内二维无旋场控制方程组[2]及其特征线方程和相容性方程[3],对特征线方程和相容性方程用差分法离散,用欧拉预估-校正法计算内点[4],用等间隙气膜内一维超音速流动的解析解进行验算。
1 扩散对称流动控制方程组
变间隙圆盘止推气体轴承结构简图如图1所示。图1中:r1为供气孔半径;r2为圆盘外半径;P*为供气压力(滞止压力);T*为供气总温(滞止温度);pa为环境背压(环境大气压);h0为平行段间隙高度常数;rs为平行段最大半径;Vr、Vz分别为气流速度的径向分量和轴向分量。不平行段壁面方程为y=y(x)。理想气体以音速从气膜入口进入圆盘间隙,在平行段内是一维扩散对称无旋流动,到达不平行段后是二维无旋流动。

图1 变间隙圆盘气体止推轴承结构Fig.1 Schematic diagram of the aerostatic thrust bearing of variable clearance
定常运动下的连续方程为

定常运动下的欧拉运动微分方程为

定常绝热运动下的能量方程(沿流线)为

热完全气体的状态方程为

等熵流动中声速关系式为
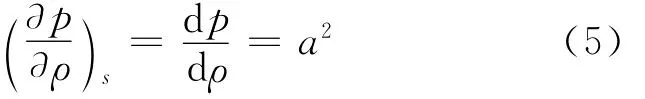
从式(2)和式(5)得

由式(1)得
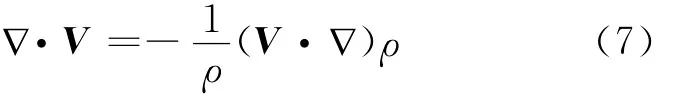
将式(6)两边点乘V,得

由无旋定义∇×V=0,有

所以
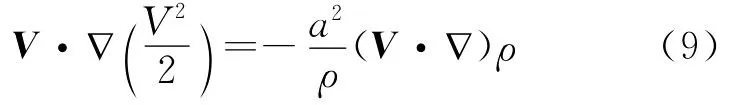
从式(7)和式(8)中约去密度项,得到理想气体等熵定常无旋流动的控制方程为

用柱坐标系表达,r轴指向半径方向,z轴垂直于气膜厚度方向,则式(10)可写成
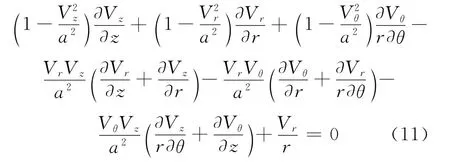
在变间隙气膜内依然有环向速度Vθ=0及对称性∂/∂θ=0,式(11)中的三维流动可以化简为气膜厚度和半径方向上的二维流动。
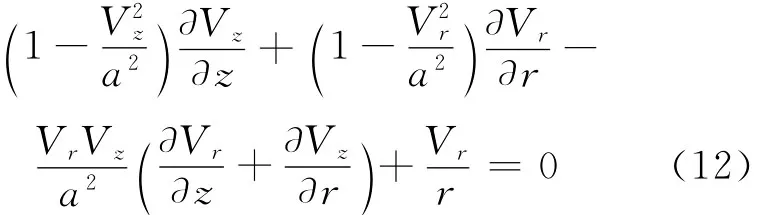
由无旋定义
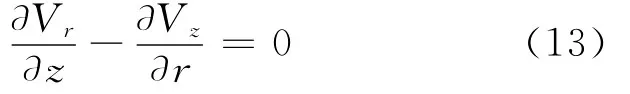
式(12)可化简为
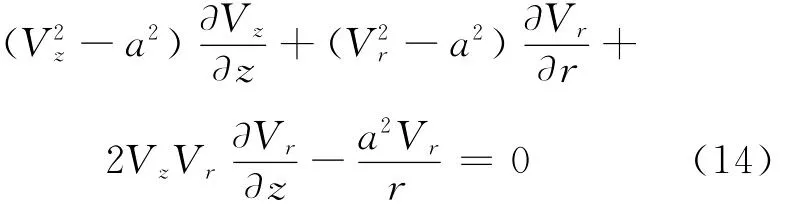
令y=z,x=r,则u=Vr,v=Vz,式(14)和式(13)变为
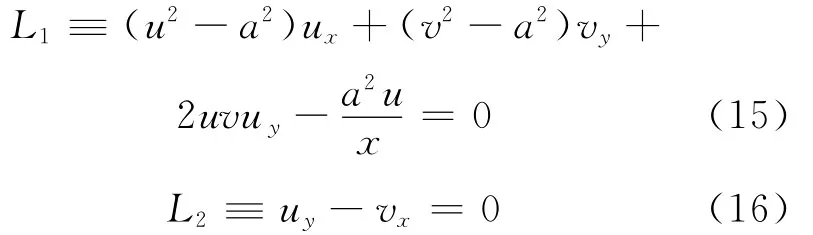
式(15)、式(16)便是变间隙圆盘止推气体轴承中气体流动控制方程组。其中,音速a是速度u和v的函数,即

所以控制方程组由两个一阶拟线性偏微分方程组成,因变量为u和v。
2 方程组特征线方程和相容性方程
u和v的全微分方程为

将式(15)、式(16)、式(18)、式(19)联立,对ux、uy、vx、vy求解,有

对于式(20)所示的方程组,导数ux不确定的条件是方程组系数为零,即

展开式(21)得

式(22)两边同时除以dx2,并令dy/dx=λ,则式(22)可改写为
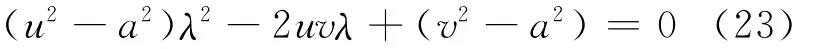
解得
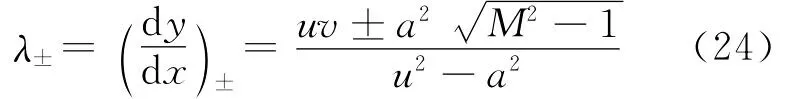
式中:下标“±”分别表示第Ⅰ族和第Ⅱ族特征线;M为马赫数,当M>1时,特征线是实数。
可见特征线法仅用于超音速流场的计算。用式(20)中的常数项替换系数行列式中的某一列,并令其等于零,可以求得沿特征线上因变量u、v之间所满足的相容关系。为避免高阶行列式运算,讨论L1与L2的线性组合,即

式中:k1、k2为任意函数。
将式(15)、式(16)代入式(25),方程改写为
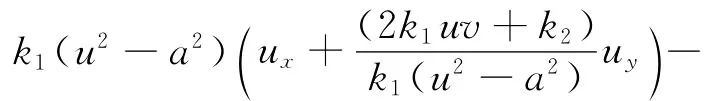
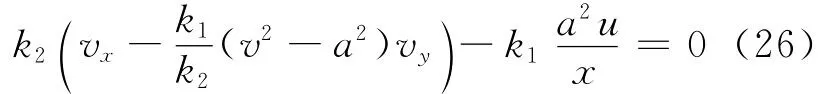
将式(26)中第1个和第2个括号内的表达式分别写成全微分du/dx和dv/dx形式,并令dy/dx=λ,即

由于原偏微分方程简化为常微分方程的曲线是特征线,因而给出的λ即是特征线的斜率
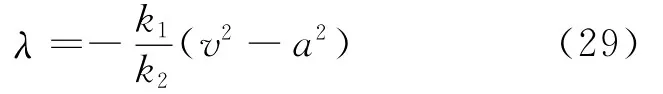
沿式(29)所示的特征线,式(26)可简化为u和v的全微分表达式,即相容关系式
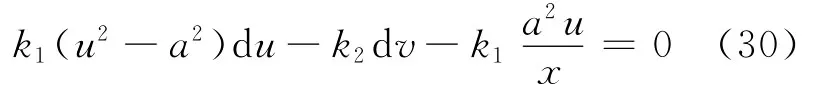
通过求k1、k2非平凡解来确定特征线的斜率λ,同时导出k1、k2的关系,故将式(30)中的k1、k2约去。由式(29)有
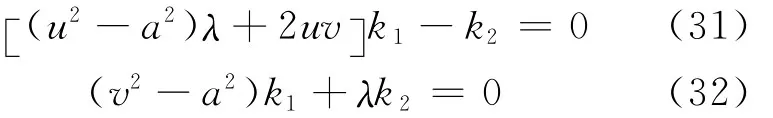
若k1和k2有不为零的解,则下式必为零,即
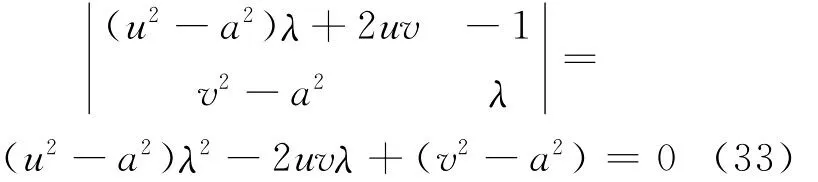
解得

式(33)确定了变气膜厚度内定常二维超音速流场中的两族特征线,由式(31)和式(32)可得

或

将上式代入式(30),得到相容关系

或
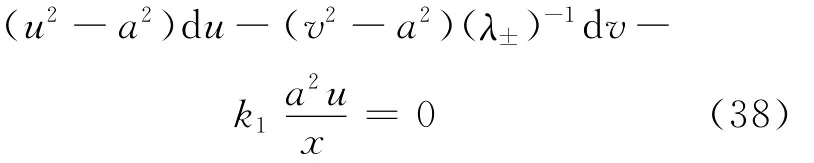
容易证明式(37)与式(38)是等价的相容关系。将特征线方程改写为简单形式,用速度矢的模及夹角V、β表示速度分量u、v,用马赫角α表示马赫数M,即

将式(39)代入式(34),解得

式(40)说明特征线上各点的切线与该点流速方向的夹角为马赫角α,按照观察者的目光顺着流速方向规定,伸向左边的为左伸特征线C+,或第Ⅰ族特征线;伸向右边的为右伸征线C-,或第Ⅱ族特征线。
3 特征线法计算流场概述
如图2所示,设平面xy中有一条非特征线的起始曲线AB,其上流动参数为已知,利用两族特征线相交形成一网格,该网格扩展到一定的区域,计算出该区域的流动参数。例如起始曲线AB上点1发出的右伸特征线C-与由点2发出的左伸征线特征线C+相交于点4,它的位置可由特征线方程式(34)求出,沿线段1-4和2-4各有一个联系du和dv的相容关系,利用此关系可以求出交点4上u和v的值。对于起始曲线AB上各离散点(包括端点A和B),均重复上述步骤,当AB上离散点距离足够小时,结果产生了一条参数已知的连续曲线DE,如此继续下去,直到图2中整个ABC区域算完为止。图2中,点C是从A发出的第Ⅱ族特征线和从点B发出的第Ⅰ族特征线的交点,而对于边界点来说一般只有一条特征线通过,对此必须补充速度与壁面相切的条件,将内点和边界点联合起来计算,这样特征线可以伸展到整个流场,从而计算出整个流场的参数。

图2 二维特征线网格及内点处理过程Fig.2 Two-dimensional characteristic line grid and interior point process
将特征线方程和相容关系写成差分方程形式,变间隙内定常二维无旋流动特征线方程和相容关系的差分方程如表1所示,平均系数法确定的有限差分系数计算方程如表2所示。

表1 变间隙气膜内超音速流动的有限差分方程Table 1 Finite difference equations of variable clearance flow within the supersonic gas film

表2 平均系数法确定的有限差分系数计算方程Table 2 Calculation equations of variable clearance flow within the supersonic gas film
4 单元处理过程
图2中点1和点2为不在一条特征线上的已知点,根据特征线差分方程式(47)、式(48)和相容关系的差分方程,采用预估-校正法可计算出点4(x4,y4)及流动参数。
4.1 预估步
设u+=u2,v+=v2,x+=x2,u-=u1,v-=v1,x-=x1。由差分方程式(47)、式(48)有
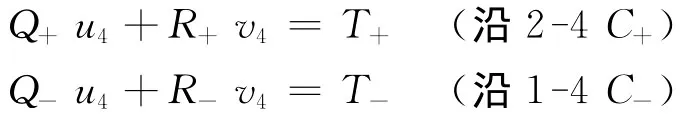
4.2 校正步
如有必要,可以使用迭代校正步,直至
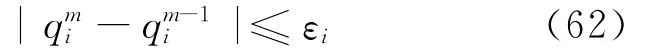
式中:qi代表x4、y4、u4、v4等参数;εi为对应于每一参数的允许误差。
数值计算表明,连续使用校正法对最终结果影响很小,一般迭代3次后结果较为稳定。
对于待解点在壁面的情形(图3),点2为已知点,由点2沿流动方向往下引出1条特征线,于壁面相交于点4,这时待解点4的位置和流动参数由两组条件决定:一是通过2-4线段的特征线方程和相容关系方程,二是壁面曲线方程及气流速度与壁面相切的条件方程,即
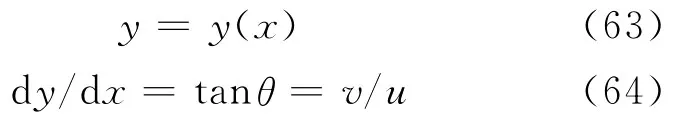
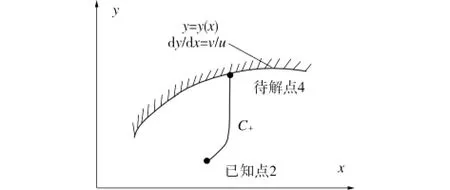
图3 壁面点处理Fig.3 Wall point processing
由式(48)和式(63)可以求出x4、y4,由式(51)和式(64)可以求出u4、v4。其预估步、校正步的步骤与内点的情形完全相同。
5 计算与验证
利用平行段一维流动的解析解来验证特征线方程和相容性方程的正确性,采用文献[1]中的例子,取r1=10 mm,r2=40 mm,P*=1 MPa,T*=293 K,此时气膜入口总压大于气膜出口截面上产生正激波的特征滞止压强,气膜入口马赫数为1,气膜内全是超音速流动,任意截面上马赫数与通气截面半径r之间的关系式[1]为
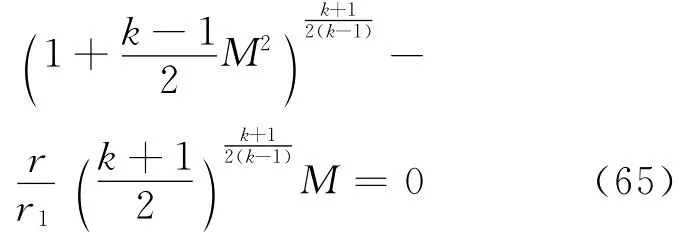
在特征线法中,给出入口处的条件为u1=u2=ccr≈312.251 8 m/s,v1=v2=0,x1=x2。已知点间距y1-y2=0.1 mm。在间隙内声速关系[5]为
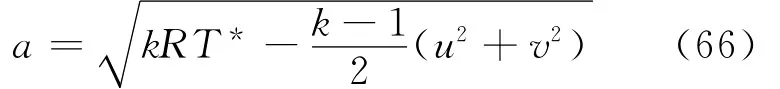
式中:k为比热比;R为气体常数。
气膜厚度h=0.2 mm,由已知点向前直接步进160次,也就是网格数是160×3。在特征线法中不能直接使用ccr的精确值,否则点1和点2在同一条特征线上,同时已知点间距不能过大,否则,式(66)根号内会出现负值。

图4 解析法与特征线法计算结果Fig.4 Contrast of analytical solution and the numerical solution characteristic line
编程后,分别用数值法和解析法(图4)对160个点上的马赫数进行计算。为了使图上的点清晰可见,仅画出了步进次数为奇数的点。从图4可看出,解析法和特征线法得到的点基本重合。由程序计算结果可知,误差小于0.01%。因此,改变起始点间距,总能得到预期数目点上的解,使得出的流动参数接近于连续函数。
6 结语
通过改变止推气体轴承等间隙的流道结构,推导出了二维无旋超音速扩散对称流动的控制方程及其特征线方程和相容性方程,用等间隙气膜内一维超音速流动的解析解验证了特征线方程和相容性方程的正确性。
[1] 郭良斌,彭宝林.理想气体条件下平行圆盘止推气体轴承承载力特性的初步研究[J].武汉科技大学学报,2011,34(1):62-68.
[2] 童秉纲,孔祥言,邓国华.气体动力学[M].北京:高等教育出版社,1990.
[3] 单鹏.多维气体动力学基础(第二版)[M].北京:航空航天出版社,2008.
[4] M J Zucrow,J D Hoffman.气体动力学(上下册)[M].王汝涌,译.北京:国防工业出版社,1984.
[5] 潘锦珊.气体动力学基础[M].北京:国防工业出版社,1989.
