基于当地摩擦因数的绝热气动管道流量特性参数计算

2011-01-23郭良斌彭宝林宣立明

武汉科技大学学报 2011年6期

郭良斌，彭宝林，王卓，宣立明

（武汉科技大学机械自动化学院，湖北武汉，430081）

在汽车制造、电子、纺织、印刷、包装、机床、食品等工业产业的自动化进程中，气动技术发挥着重要的作用[1－3]。为了设计出优化的气动回路与系统，需要准确地把握每个气动元件的流量特性[4]。在气动系统中，管道将各种元器件连接成一个系统，把压缩空气从压缩机输送到终端用气设备以传递动力[5]。随着气动元件的小型化和配管的延长，气动管道的流量特性日渐重要[6]。气动系统节能日益受到关注[7－10]，正确把握气动主管道和各分支管道的流量特性，选择功率匹配的空气压缩机进行合理的流量管理是气动系统节能的首要工作[11]。

对绝热气动管道流量特性的计算，常采用经典一维绝热摩擦管流理论[12－13]，某一特定管道的平均摩擦因数是计算前需要确定的一个基本参数，尽可能准确地获得平均摩擦因数的具体数值，将有助于提高管道流量特性的计算精度。文献[14]提出一种利用当地摩擦因数计算绝热气动管道平均摩擦因数的新方法，以该方法确定的平均摩擦因数计算出的不同长度管道声速流导／管道截面积比值，与按照ISO 6358测试方法得到的实验拟合曲线相吻合，初步验证了该方法的可行性[15]。气动管道的流量特性可以用壅塞流态下的有效截面积S和临界压力比b两个特性参数完整地表达[4]。为此，本文推导以管道进口截面速度因数为自变量的流量特性参数函数S／A（管道有效截面积与横截面积之比）和临界压力比b的基本表达式，分析其特性，并用上述新方法得到的平均摩擦因数直接计算出总压为0.6 MPa、总温为300 K、长度为1～50 m、内径为2.5～9 mm的尼龙管的流量特性参数S和b，发现S和b的理论计算值与经验推荐值相吻合。

1 临界管道数学模型描述

图1 等截面绝热有摩擦一维管道模型Fig.1 One－dimensional adiabatic frictional flow in a duct of constant cross－section

等截面直管绝热有壁面摩擦的一维管道模型如图1所示。图1中，进口气流总压为P0，进口气流总温为T0，出口反压力为pb。设管道进口的气流总压和总温不变，出口反压力pb可变化。临界管道指管道出口马赫数达到临界声速，此时管道达到最大通流能力，处于壅塞状态，分析时可以不考虑管道出口反压力对管中气体流动的影响。设不论管长怎么变化，反压力总能使管道出口达到临界声速。

临界状态时管道出口截面上的速度因数λout为1，这样可列出管道进口截面上的速度因数λin与平均摩擦因数的关系式[16]：

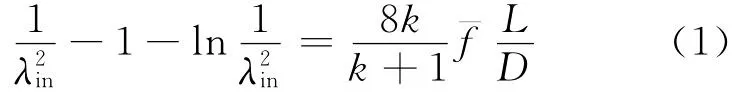
式中：为管道的平均摩擦因数；L／D为管道长径比；k为比热比。

管道平均摩擦因数的物理定义式为

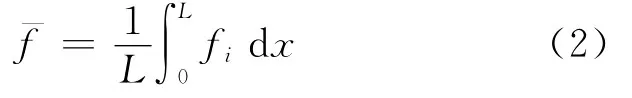
式中：fi为各截面上摩擦因数，即当地摩擦因数，它取决于管内各截面上雷诺数和管道的相对粗糙度。

同一管道的不同截面上，气流速度和动力黏度不同，不同截面上的摩擦因数（即当地摩擦因数）各不相同；平均摩擦因数代表整个管道对气流的摩擦效应，通过平均摩擦因数的物理定义式可建立起整个管道的平均摩擦因数和管道不同截面上当地摩擦因数的有机联系。采用预估－校正解法，利用Keenan的实验结果可直接计算出大多数绝热气动管道的平均摩擦因数[14]，计算出给定进口总压、总温、管径、长径比以及管道材质条件下的平均摩擦因数后，可由式（1）计算出临界管道的进口速度因数λin。管道壅塞状态下的质量流量为[16]

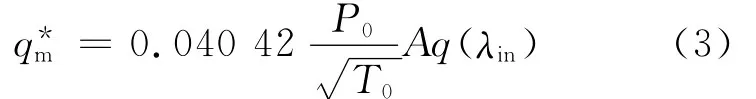
式中：A为管道的横截面积，m2；q（λin）为气体动力学流量函数。

设某一特定管道的有效截面积为S，则根据有效截面积的定义[17]，临界状态下该管道的质量流量为

式中：p1为管道进口截面上的静压力，Pa；T1为管道进口截面上的静温度，K。

对比式（3）、式（4）可知：

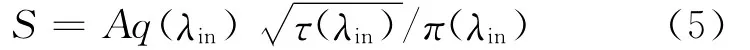
式中：τ（λin）、π（λin）分别以λin为自变量的气体动力学函数。

临界状态下该管道出口截面上的静压力为

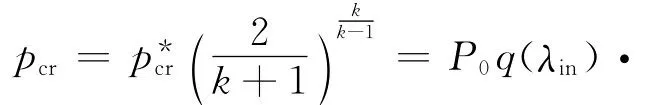
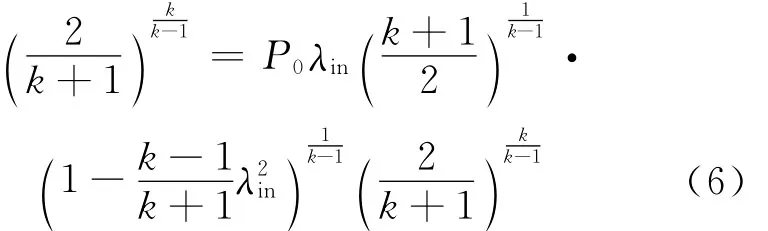
若管外反压力pb等于pcr，则管道为临界流动状态；若管外反压力pb小于pcr，则管道为超临界流动状态，但管内流动参数与临界状态时相同，反压力只影响出口外的流动而不影响管内的流动参数。若管外反压力pb大于pcr，则管内为亚临界流动状态，本文仅考虑临界工况。

临界压力比b的定义为元件内亚声速流动和声速流动分界点的下游与上游管道内的静压力之比[17]。若把气动管道也看作一种气动元件，则气动管道的临界压力比b可类似定义为临界管道出口截面上的静压力pcr与进口截面上的静压力pin之比。

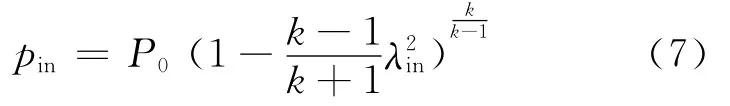
这样由式（6）、式（7）可推出：

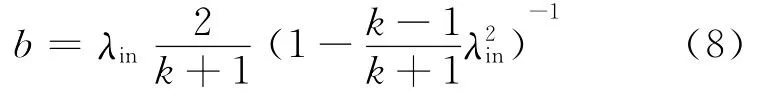
2 流量特性参数函数的性质

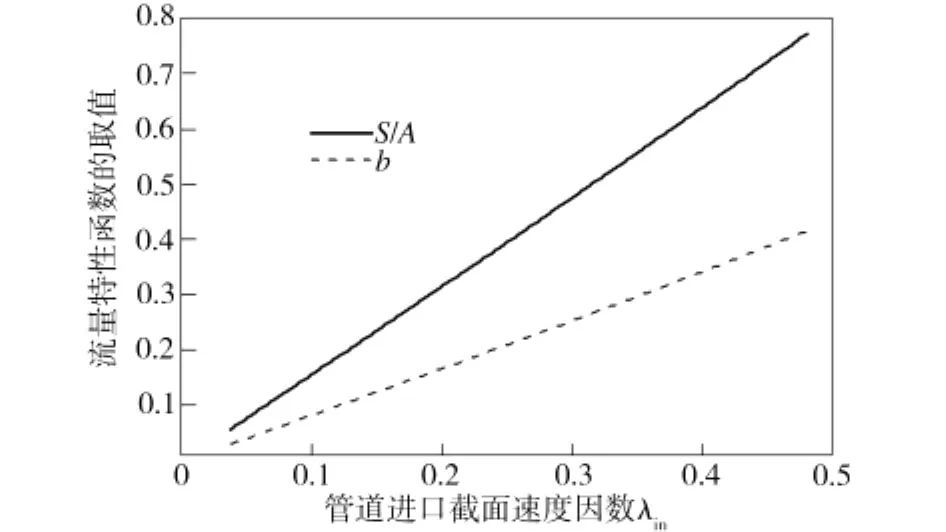
图2 流量特性参数函数曲线Fig.2 Curves of parameter function of flow－rate characteristics

将式（5）写成无量纲的形式：

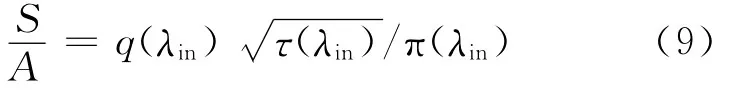
由式（8）、式（9）可知，S／A和b可看作是以管道进口截面速度因数λin为自变量的流量特性参数函数。不失一般性，取长度为1～50 m的尼龙管，供气总压为0.6 MPa，总温为300 K，内径为2.5～9 mm的绝热气动管道，进口截面速度因数的理论计算值为0.037 17～0.478 7。按式（8）、式（9）绘制的流量特性参数函数曲线如图2所示。由图2可看出，在λin的取值范围内，流量特性参数函数S／A和b基本上都是管道进口截面速度因数λin的线性函数。当进口截面的速度因数为0.037 17～0.478 7时，S／A值为0.058～0.772；b值为0.031～0.416。

3 理论计算值与经验推荐值的比较

3.1 标准长度尼龙管的有效截面积S

表1为标准长度尼龙管有效截面积的计算值与经验值。文献[17]给出了1 m标准长度不同管内径尼龙管有效截面积的经验推荐值S0，如表1第2列所示。表1第3列是在总压为0.6 MPa、总温为300 K的条件下，从当地摩擦因数计算得到的标准长度尼龙管的平均摩擦因数。表1第4列是采用第3列的数据得到的标准长度尼龙管有效截面积的理论计算值ST。表1第5列的相对误差用下式计算：

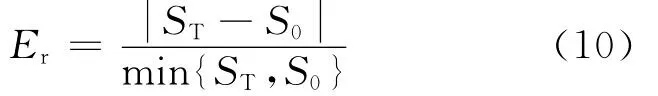
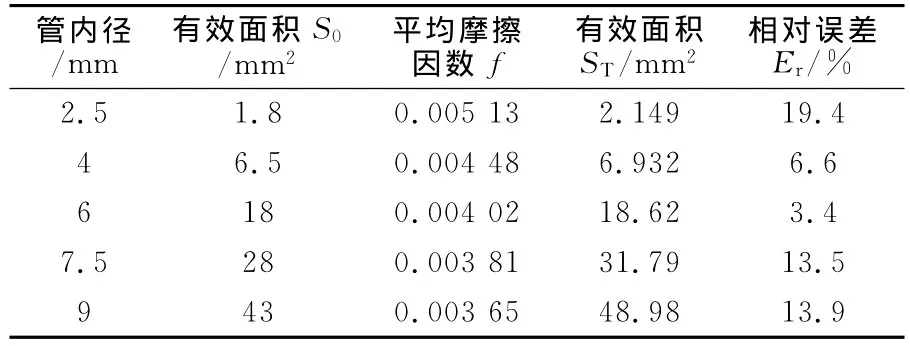
表1 标准长度尼龙管有效截面积的计算值与经验值Table 1 Theoretical and empirical values of effective sectional area of nylon duct with standard length

由表1可看出，采用新方法计算的标准长度尼龙管有效截面积ST与经典文献给出的经验推荐值S0基本相同，最大误差在20%以内。另外，表1第2列不同管径标准长度尼龙管的经验推荐值S0全部小于第4列的理论计算值ST，相对保守，这有利于增加系统设计的可靠性。

3.2 任意长度尼龙管的有效截面积S

任意长度尼龙管有效截面积的经验计算公式[17]为

式中：Se为按经验公式（11）计算的任意长度尼龙管的有效截面积，mm2；S0为1 m的标准长度尼龙管的有效截面积，mm2；L为实际管长，m。

图3为在总压为0.6 MPa、总温为300 K的条件下，采用新方法直接计算的任意长度尼龙管的有效截面积ST与采用经验公式（11）计算的Se的相对误差曲线。相对误差的计算公式与式（10）类似。由图3可看出，对管内径为2.5 mm的尼龙管，两种方法计算的任意长度尼龙管的有效截面积数值几乎相同，最大误差不超过5%。随着管内径的增大，相同长度尼龙管有效截面积的相对误差逐渐增大，管内径为9 mm的尼龙管最大误差约为30%。大量计算表明，在绝大多数情况下，采用新方法直接计算的任意长度尼龙管的有效截面积ST大于采用经验公式（11）计算的Se，这表明有效截面积经验计算公式（11）也相对保守，同样有利于增加系统设计的可靠性。

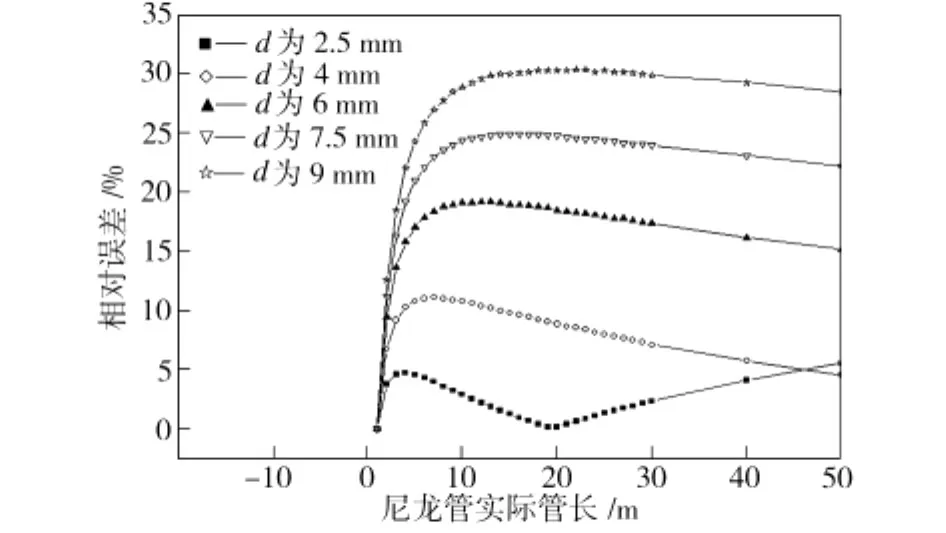
图3 两种方法计算有效截面积的相对误差Fig.3 Relative error of effective sectional area with two different methods

3.3 任意长度尼龙管的临界压力比b

任意长度尼龙管的临界压力比的经验计算公式[6]为

式中：be为按经验公式（12）计算的任意长度尼龙管的临界压力比；C0为1 m的标准长度尼龙管的声速流导，m3／（s·Pa）；d为管内径，m。

声速流导C0的计算公式[17]为

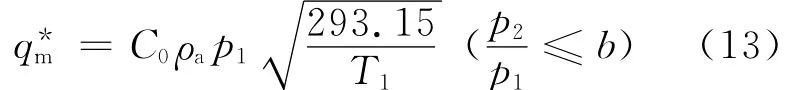
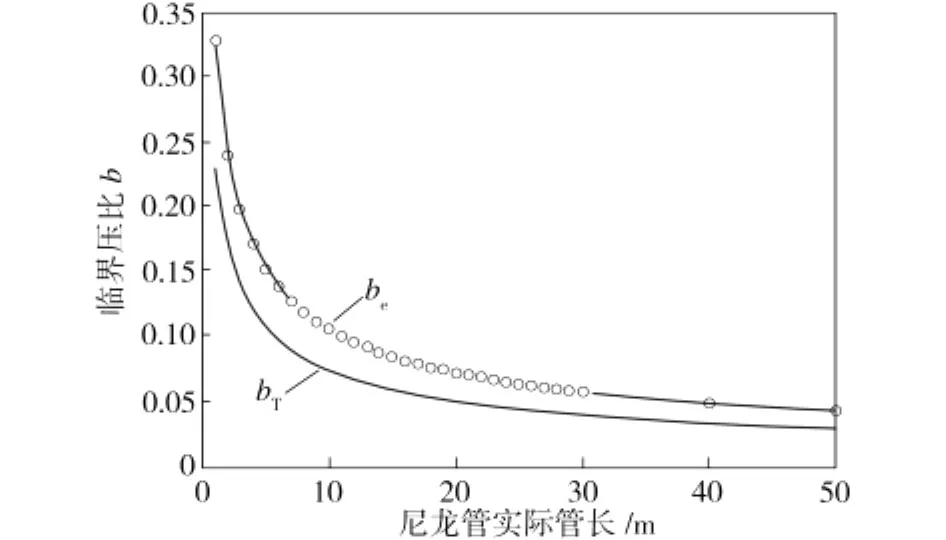
图4 两种方法计算的临界压力比bFig.4 Critical pressure ratio with two different methods

图4为在总压为0.6 MPa、总温为300 K的条件下，采用新方法直接计算内径为2.5 mm任意长度尼龙管的临界压力比bT与采用经验公式（12）计算的be的曲线对比。由图4可看出，采用新方法直接计算任意长度尼龙管的临界压力比bT值小于采用经验公式（12）计算的be值。但每个计算点两者相对误差基本上都等于40%，因此两条曲线的变化趋势相同。对其他管内径（4、6、7.5、9 mm内径）的计算结果与图4也十分类似。

流量特性参数的理论计算值与经验曲线变化趋势相同，且计算值与经验值相吻合，表明新方法可以在相当程度上反映气动管道流量特性参数变化的物理本质。