高压下β硼电输运行为中的晶界效应

杨 洁，张冬梅

(1.空军航空大学基础部，吉林 长春130022；2.吉林大学 原子与分子物理研究所，吉林 长春 130012)

1 前言

多晶样品的晶界不同于单晶，因为这些晶界可能在决定材料的物理性质方面起主要作用.因此，探究晶界如何显著地影响材料的电输运行为非常重要.单频交流电阻测量方法可用于对单晶和纯的流体样品的研究，但对多晶或液体混合物样品却不适用.对后者而言，变频交流阻抗谱方法在几十年前就广泛应用于分离晶粒内部和晶界对总阻抗的贡献[1，2]，但是这种方法还未清晰地揭露出晶界在这些复杂样品中起何种作用，对晶界贡献的解释仍有分歧.如Shankland等人[1]以及后来的Kariya等人[3]发现，对橄榄石而言，晶界为提高其电导率；相反，Schock等人[4]研究了高压下的多晶橄榄石粉末，认为晶界电导率对样品总的电导率有非常小的影响.此外，Haak[5]认为在560℃到1150℃范围内，多晶橄榄石的电导率比单晶高；并且，单晶和多晶橄榄石样品的电导率在1400℃左右会聚到一点，他认为此种现象可能归因于离子传播路径的增加.可见，所有对橄榄石电学性质的研究已经表明，晶界对总电阻有贡献，但此贡献对总阻抗而言是正面亦或负面仍不确定.随着变频交流阻抗谱方法的发展，晶粒和晶界贡献的分离已可通过测量它们的相对比率来实现[6-8].

在材料科学领域，硼及富硼化合物占有很重要的位置，因为富含硼的物质有很高的硬度[9]和高温超导等现象[10].基于以上这些原因，硼成为最近几十年实验和理论研究的热点.Werheit等人[11]认为硼样品中的载流子为空穴，传输模式为跳跃传导.Erements等人[12]通过实验证明，β硼在几个开尔文的温度下将由半金属变为超导体；而Papacnstantopoulos等人[13]则通过第一性原理计算发现了β硼的超导现象；赵等人[14]利用第一性原理研究了β硼的压致金属化.尽管对β硼的研究已有很多，但晶界对β硼电输运性质的影响几乎未被讨论过.基于此，本文利用金刚石对顶砧变频交流阻抗谱测量方法，进行了高压下多晶β硼样品的实验研究，旨在揭露晶界在总阻抗中的作用及晶界处电输运的传导机制.β硼具有较大的斜方结构，每个晶胞里包含105个硼原子，二十面体位于斜面体的每一个顶角处和每一个边的中心，中间的团簇沿对角线排列.

2 实验

本工作采用Mao-Bell型DAC产生高压，交流阻抗谱测量采用Solartron1260二终端频响分析仪.电极的制备过程在以前的工作中有详细的介绍[15].频率范围为10μHz～30MHz，交流电压选用0.1V，测量过程中保持室内温度稳定.实验最高压力为27.5GPa.

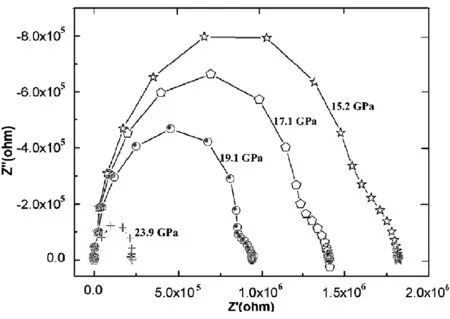
图1 高压下β硼的阻抗谱

3 实验结果及分析

图1展示的是不同压力下β硼的交流阻抗谱，压力点分别为15.2，17.1，19.1，23.9GPa，横轴为阻抗实部，纵轴为阻抗虚部.图谱左侧为高频部分.电阻值为曲线与横轴的截距.最好的情况下，阻抗谱会展示出三部分分离的贡献，高频区为晶粒贡献，中频区为晶界贡献，低频区为电极贡献[16].然而，本实验只出现两个半圆弧，分别对应着两个传导过程：左边为晶粒传导，右边为晶界传导[16]，而电极的贡献没有观察到.

由图1可以明显的发现以下三点：(1)晶粒电阻和晶界电阻均随压力而减小，表明带隙随压力而减小；(2)23.9GPa处的阻抗谱与其它三个压力点明显不同，对应着β硼电导率的显著增加，可归因于晶粒表面缺陷的变化；(3)23.9GPa处，晶界传导几乎消失.在23.9GPa阻抗谱独特的模式依赖于粒子间的范德瓦尔斯力(FVDW).

依据Hamaker[17]的理论，FVDW不仅存在于单独的原子或分子间，而且存在于粒子之间.Hamaker利用London推测的附加假定[18]，获得了FVDW的数学表达式，对于距离H，由两种不同物质1和2组成，半径分别为R1和R2的两个固体球形粒子，FVDW表示为：

FVDW=AR/6H2

(1)

其中，A=π2q1q2λ1，2，为Hamaker常数，R为半径的几何平均值，R=R1R2/2(R1+R2).在A的表达式中，q1和q2分别为两种相互作用粒子的原子密度，λ1，2为London-范德瓦尔斯常数，其值依赖于原子数量.对于本实验，A和R值均不改变，因此，FVDW只和H2的倒数成比例关系.

存在于两种粒子间的范德瓦尔斯力属短程作用力，当两种粒子的间距足够小时出现.在我们的模型中，β硼晶粒属于此类粒子.随着压力的增加，晶粒间距逐渐减小，其表面悬键开始相互作用.随着距离的减小，这种相互作用逐渐增强，当压力达23.9GPa时导致范德瓦尔斯力和悬键相互作用的出现.这使得β硼晶界对载流子的散射减弱，导致23.9GPa时阻抗特性的异常变化.这一基本的物理图象对β硼样品是有效的，也可能适用于所有种类的多晶样品，电阻变化的幅度可能依赖于晶粒表面缺陷、悬键的种类和数量甚至位错的类型.

为深入分析晶界在电输运性质中的作用，图2给出了不同压力下阻抗虚部随频率的变化关系，由此可得出弛豫频率.虚部随压力迅速减小，表明晶界对β硼电输运的贡献减弱.弛豫频率依赖于载流子状态，压力会使β硼载流子态发生不对称，进而影响弛豫频率.阻抗虚部随频率的变化表现为两个相反的趋势，大的趋势表现为铁核导性特征，小的频率趋势则表现为典型的容性特征[19].因此，β硼阻抗虚部主要为导性特征，同时伴随着小的容性部分.

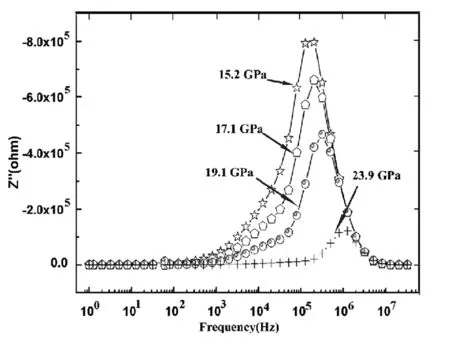
图2 高压下β硼阻抗虚部随频率的变化

利用Zview阻抗分析软件对实验数据进行拟合，可以得到晶粒电阻Rg和晶界电阻Rgb.设RT为总电阻，即RT=Rg+Rgb，则Rgb/RT随压力的变化(如图3所示)反映了晶界电阻对总电阻的贡献.

当压力达23.9GPa时，图3中的曲线出现微小的下降，此时晶界对总电阻的贡献仅为7%.前面已经提到，在23.9GPa处，β硼晶界对电荷载流子的散射减弱，晶界对载流子的较小贡献可解释如下：晶界处存在许多缺陷能级，例如空位，纠缠态等局域态的电荷陷阱能级，它们将捕获晶体内的电荷载流子.在纯的β硼中空穴传输是主要的传导机制，因此在其晶界处的陷阱能级将从近临的晶粒处俘获空穴载流子，从而导致晶粒内部空穴的消耗和晶粒边界处载流子的积累.因此体电阻对总电阻的贡献比晶界电阻大.

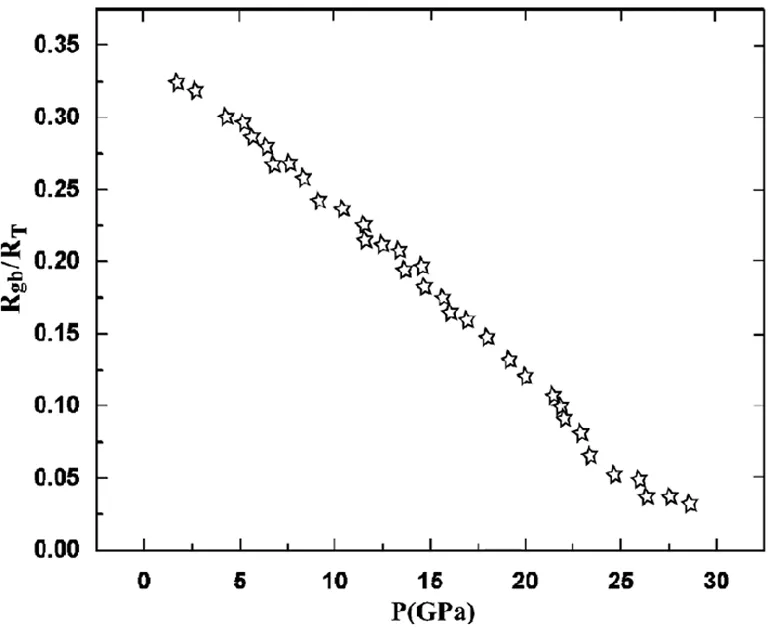
图3 β硼中Rgb/RT随压力的变化关系

4 结论

本文利用交流阻抗谱测量方法，系统讨论了高压下晶界效应对β硼电输运性质的影响，结果表明：晶粒电阻和晶界电阻均随压力逐渐减小，晶粒电阻对β硼总阻抗起主要作用；晶界电阻对总电阻的贡献随压力逐渐减小，当压力达23.9GPa时，随着范德瓦尔斯力及晶界相互作用的出现，晶界传导几乎消失.

[1]T.J.ShanklandandH.S.Waff.Partialmeltingandelectricalconductivityanomaliesintheuppermantle[J].JournalofGeophysicalResearch.1977，82:5409-5417.

[2]J.FleigandJ.Maier.Microcontactimpedancemeasurementsofindividualhighlyconductivegrainboundaries:GeneralaspectsandapplicationtoAgCl[J].PhysicalChemistryChemicalPhysics，1999，1:3315-3320.

[3]K.A.KariyaandT.J.Shankland.Electricalconductivityofdrylowercrustalrocks[J].Geophysics，1983，48:52-61.

[4]R.N.Schock，A.G.Duba，H.C.Heard，andH.D.Stromberg.Theelectricalconductivityofpolycrystallineolivineandpyroxeneunderpressure[J].High-PressureResearch:ApplicationsinGeophysics，1977：39.

[5]V.Haak.inHigh-PressureResearchesinGeoscience[G]//W.Schreyer，editor.E.Schweizerbart'scheVerlagsbuchhandlung，Stuttgart，1982：407.

[6]J.E.Bauerle.Studyofsolidelectrolytepolaizatinbyacomplesadmittancemethod[J].JournalofPhysicsandChemistrofSolids，1969，30(12):2657-2670.

[7]E.LilleyandJ.E.Strutt.BulkandGrainBoundaryIonicConductivityinPolycrystalline''-Alumina[J].PhysicaStatusSolidiA，1979，54(2):639-650.

[8]M.J.Verkerk，B.J.Middelhuis，andA.J.Burggraaf.Effectofgrainboundaryesontheconductivityofhigh-purityZrO2-Y2O3ceramics[J].SolidStateIonics,1982，6(2):159-170.

[9]V.V.Brazhkin，A.G.Lyapin，andR.J.Hemley.Harderthandiamond:dreamsandreality[J].PhilosophicalMagazineA，2002，82(2):231-253.

[10]J.Nagamatsu，N.Nakagawa，T.Muranaka，Y.Zenitani，andJ.Akimitsu.Superconductivityat39Kinmagnesiumdiboride[J].Nature，2001，410:63-64.

[11]H.WerheitandH.G.Leis.OntheConductivityMechanismof-RhombohedralBoron[J].PhysicaStatusSolidiB，1970，41(1):247-253.

[12]M.I.Eremets，V.V.Struzhkin，H.K.Mao，andR.J.Hemley.SuperconductivityinBoron[J].Science，2001，293:272-274.

[13]D.A.PapaconstantopoulosandM.J.Mehl.First-principlesstudyofsuperconductivityinhigh-pressureboron[J].PhysicalReviewB，2002，65:172510.

[14]J.J.ZhaoandJ.P.Lu.Pressure-inducedmetallizationinsolidboron[J].PhysicalReviewB，2002，66:092101.

[15]C.Y.He，C.X.Gao，Y.Z.Ma，M.Li，A.M.Hao，X.W.Huang，B.G.Liu，D.M.Zhang，C.L.Yu，G.T.Zou，Y.C.Li，H.Li，X.D.Li，andJ.Liu.Insituelectricalimpedancespectroscopyunderhighpressureondiamondanvilcell[J].AppliedPhysicsLetter，2007，91:092124.

[16]M.K.Kazimierczuk，G.Sancineto，G.Grandi，U.Reggiani，andA.Massarini.IEEETrans[J].Magn，1999，35:4185.

[17]H.C.Hamaker.TheLondon-vanderWallsattractionbetweensphericalparticles[J].Physica.1937，4(10):1058-1072.

[18]F.London.Thegeneraltheoryofmolecularforces[J].TransactionsoftheFaradaySociety，1937，33:8b.

[19]M.M.BülbülandS.Zeyrek.Frequencydependentcapacitanceandconductance-voltagecharacteristicsofAl/Si3N4/p-Si(100)MISdiodes[J].MicroelectronicEngineering，2006，83(11-12):2522-2526.